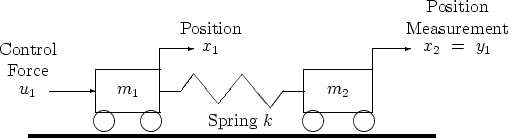
Как пример системы с обратной связью неопределенными параметрами, считайте 2D корзину "системой" Сравнительного теста ACC [13] состоящий из двух лишенных трения корзин соединенный к пружине показанный можно следующим образом.
Эталонная тестовая задача ACC
Системе показали модель блок-схемы ниже, где отдельные корзины имеют соответствующие передаточные функции.
Параметры m1, m2, и k сомнительны, равны одному плюс или минус 20%:
m1 = 1 ± 0.2 m2 = 1 ± 0.2 k = 1 ± 0.2
"Системная Блок-схема y1 2D Корзины" Сравнительного теста ACC = P (s) u1
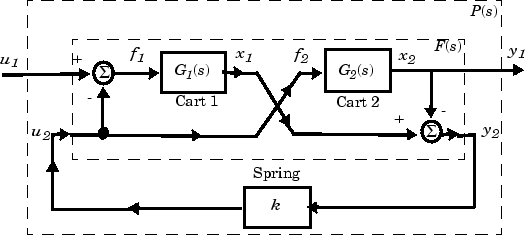
Верхний блок пунктирной линии имеет матрицу передаточной функции F (s):
Этот код создает неопределенную системную модель P показанный выше:
m1 = ureal('m1',1,'percent',20); m2 = ureal('m2',1,'percent',20); k = ureal('k',1,'percent',20); s = zpk('s'); G1 = ss(1/s^2)/m1; G2 = ss(1/s^2)/m2; F = [0;G1]*[1 -1]+[1;-1]*[0,G2]; P = lft(F,k);
Переменная P объект неопределенного пространства состояний (USS) SISO с четырьмя состояниями и тремя неопределенными параметрами, m1, m2, и k. Можно восстановить номинальный объект с командой:
zpk(P.nominal)
ans =
1
-------------
s^2 (s^2 + 2)
Continuous-time zero/pole/gain model.
Если неопределенная модель P (s) имеет контроллер отрицательной обратной связи LTI
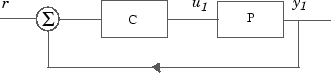
затем можно сформировать контроллер и систему с обратной связью y1 = T (s) u1 и просмотреть переходной процесс системы с обратной связью на временном интервале от t=0 до t=0.1 для случайной выборки Монте-Карло пяти комбинаций трех неопределенных параметров k, m1, и m2 использование этого кода:
C=100*ss((s+1)/(.001*s+1))^3; % LTI controller T=feedback(P*C,1); % closed-loop uncertain system step(usample(T,5),.1);
