Разложите неопределенные объекты на бесспорный фиксированный, и нормировал неопределенные части
[M,Delta] = lftdata(A); [M,Delta] = lftdata(A,List); [M,Delta,Blkstruct] = lftdata(A); [M,Delta,Blkstruct,Normunc] = lftdata(A);
lftdata разлагает неопределенный объект на фиксированную определенную часть и нормированную неопределенную часть. lftdata может также частично разложить неопределенный объект на неопределенную часть и нормированную неопределенную часть. Неопределенные объекты (umat, ufrd, uss) представлены как бесспорные (т.е. не - сомнительный) объекты в обратной связи с диагональными блоком конкатенациями неопределенных элементов.
[M,Delta] = lftdata(A) разделяет неопределенный объект A в определенный объект M и нормированный неопределенный матричный Delta таким образом, что A равно lft(Delta,M), как показано ниже.
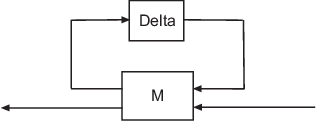
Если A umat, затем M будет double; если A uss, затем M будет ss; если A ufrd, затем M будет frd. Во всех случаях, Delta umat.
[M,Delta] = lftdata(A,List) разделяет неопределенный объект A в неопределенный объект M, в обратной связи с нормированным неопределенным матричным Delta. List ячейка (или char) массив имен неопределенных элементов A это составляет Delta. Вся другая неопределенность в A остается в M.
lftdata(A,fieldnames(A.Uncertainty)) совпадает с lftdata(A).
[M,DELTA,BLKSTRUCT] = lftdata(A) возвращает N-by-1 массив структур BLKSTRUCT, где BLKSTRUCT(i) описывает i- th нормировал неопределенный элемент. Это описание неопределенности может быть передано непосредственно структурированной аналитической функции сингулярного значения низкого уровня mussv.
[M,DELTA,BLKSTRUCT,NORMUNC] = lftdata(A) возвращает массив ячеек NORMUNC из нормированных неопределенных элементов. Каждый нормированный элемент имеет 'Normalized' добавленный к его настоящему имени, чтобы избежать беспорядка. Обратите внимание на то, что lft(blkdiag(NORMUNC{:}),M) эквивалентно A.
Создайте неопределенный матричный A 3 неопределенными параметрами p1, p2 и p3. Можно анализировать A в его определенное, M, и нормированные неопределенные части, Delta.
p1 = ureal('p1',-3,'perc',40);
p2 = ucomplex('p2',2);
A = [p1 p1+p2;1 p2];
[M,Delta] = lftdata(A);
Можно смотреть различие между исходной неопределенной матрицей, A, и результат, сформированный путем объединения двух результатов разложения.
simplify(A-lft(Delta,M))
ans =
0 0
0 0
M
M =
0 0 1.0954 1.0954
0 0 0 1.0000
1.0954 1.0000 -3.0000 -1.0000
0 1.0000 1.0000 2.0000
Можно проверять норму худшего случая неопределенной части с помощью wcnorm. Сравните выборки неопределенной части A с неопределенным матричным A.
wcn = wcnorm(Delta)
wcn =
lbound: 1.0000
ubound: 1.0001
usample(Delta,5)
ans(:,:,1) =
0.8012 0
0 0.2499 + 0.6946i
ans(:,:,2) =
0.4919 0
0 0.2863 + 0.6033i
ans(:,:,3) =
-0.1040 0
0 0.7322 - 0.3752i
ans(:,:,4) =
0.8296 0
0 0.6831 + 0.1124i
ans(:,:,5) =
0.6886 0
0 0.0838 + 0.3562i
Создайте неопределенный матричный A 2 неопределенными действительными параметрами v1 и v2 и создайте неопределенную систему G использование A как динамические матричные и простые матрицы для ввода и вывода.
A = [ureal('p1',-3,'perc',40) 1;1 ureal('p2',-2)];
sys = ss(A,[1;0],[0 1],0);
sys.InputGroup.ActualIn = 1;
sys.OutputGroup.ActualOut = 1;
Можно анализировать G в определенную систему, Msys, и нормированная неопределенная матрица, Delta. Вы видите от Msys то, что это бесспорно и что группы ввода и вывода были настроены.
[Msys,Delta] = lftdata(sys);
Msys
a =
x1 x2
x1 -3 1
x2 1 -2
b =
u1 u2 u3
x1 1.095 0 1
x2 0 1 0
c =
x1 x2
y1 1.095 0
y2 0 1
y3 0 1
d =
u1 u2 u3
y1 0 0 0
y2 0 0 0
y3 0 0 0
Input groups:
Name Channels
ActualIn 3
p1_NC 1
p2_NC 2
Output groups:
Name Channels
ActualOut 3
p1_NC 1
p2_NC 2
Continuous-time model.
Можно вычислить норму по выборкам различия между исходной неопределенной матрицей и результатом, сформированным путем объединения Msys и Delta.
norm(usample(sys-lft(Delta,Msys),'p1',4,'p2',3),'inf')
ans =
0 0 0
0 0 0
0 0 0
0 0 0
Создайте неопределенный матричный A и выведите неопределенный матричный B с помощью неявного-к-явному преобразования, imp2exp. Обратите внимание на то, что B имеет 2 неопределенных параметра R и K. Можно анализировать B в определенный, M, и нормированные неопределенные части, Delta.
R = ureal('R',1,'Percentage',[-10 40]);
K = ureal('K',2e-3,'Percentage',[-30 30]);
A = [1 -R 0 -K;0 -K 1 0];
Yidx = [1 3];
Uidx = [4 2];
B = imp2exp(A,Yidx,Uidx);
[M,Delta] = lftdata(B);
Та же операция может быть выполнена путем определения неопределенных параметров, K и R, быть извлеченным.
[MK,DeltaR] = lftdata(B,'R');
MK
UMAT: 3 Rows, 3 Columns
K: real, nominal = 0.002, variability = [-30 30]%, 2 occurrences
[MR,DeltaK] = lftdata(B,'K');
MR
UMAT: 4 Rows, 4 Columns
R: real, nominal = 1, variability = [-10 40]%, 1 occurrence
simplify(B-lft(Delta,M))
ans =
0 0
0 0
simplify(B-lft(DeltaR,MK))
ans =
0 0
0 0
simplify(B-lft(DeltaK,MR))
ans =
0 0
0 0
Выборка и смотрит неопределенную часть, а также различие между исходной неопределенной матрицей и произведенной матрицей. Вы видите результат, сформированный путем объединения двух результатов разложения.
[Mall,Deltaall] = lftdata(B,{'K';'R'});
simplify(Mall)-M
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0