Начальные условия для транспонированной прямой формы II реализаций фильтра
z = filtic(b,a,y,x)
z = filtic(b,a,y)
z = filtic(b,a,y,x) находит начальные условия, z, для задержек транспонированной прямой формы II реализаций фильтра, данных мимо выходных параметров y и входные параметры x. Векторы b и a представляйте числитель и коэффициенты знаменателя, соответственно, передаточной функции фильтра.
Векторы x и y содержите новый ввод или вывод сначала и самый старый ввод или вывод в последний раз.
где n length(b)-1 (порядок числителя) и m length(a)-1 (порядок знаменателя). If length(x) меньше n, filtic клавиатуры это с нулями к длине n; если length(y) меньше m, filtic клавиатуры это с нулями к длине m. Элементы x вне x(n-1) и элементы y вне y(m-1) являются ненужными так filtic игнорирует их.
Выведите z вектор-столбец длины, равной большему из n и m. z описывает состояние задержек, данных прошлые входные параметры x и мимо выходных параметров y.
z = filtic(b,a,y) принимает что вход x 0 в прошлом.
Транспонированную прямую форму II структур показывают на следующем рисунке.
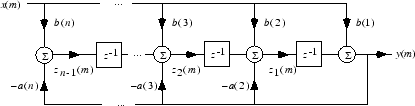
n 1 порядок фильтра.
filtic работает и на действительные и на комплексные входные параметры.
Если любой из входных параметров yXB, или a не вектор (то есть, если какой-либо аргумент является скаляром или массивом), filtic дает следующее сообщение об ошибке:
Requires vector inputs.
filtic выполняет противоположное разностное уравнение, чтобы получить задержку, утверждает z.
[1] Оппенхейм, A.V., и Р.В. Шафер, Обработка сигналов Дискретного времени, Prentice Hall, 1989, стр 296, 301-302.