goertzel
Дискретное преобразование Фурье с алгоритмом Goertzel второго порядка
Синтаксис
dft_data = goertzel(data)
dft_data = goertzel(data,freq_indices)
dft_data = goertzel(data,freq_indices,dim)
Описание
dft_data = goertzel(data) возвращает дискретное преобразование Фурье (DFT) входных данных, data, использование алгоритма Goertzel второго порядка. Если data матрица, goertzel вычисляет ДПФ каждого столбца отдельно. Можно задать типы данных как двойную или одинарную точность.
dft_data = goertzel(data,freq_indices) возвращает ДПФ для индексов частоты freq_indices. Значения freq_indices может быть любое целое число или часть.
dft_data = goertzel(data,freq_indices,dim) вычисляет ДПФ матричного data по измерению dim.
Примеры
Оцените телефонные частоты клавиатуры
Оцените частоты тона, сгенерированного путем нажатия 1 кнопки на телефонной клавиатуре.
Номер 1 производит тон с частотами 697 и 1 209 Гц. Сгенерируйте 205 выборок тона с частотой дискретизации 8 кГц.
Fs = 8000; N = 205; lo = sin(2*pi*697*(0:N-1)/Fs); hi = sin(2*pi*1209*(0:N-1)/Fs); data = lo + hi;
Используйте алгоритм Goertzel, чтобы вычислить ДПФ тона. Выберите индексы, соответствующие частотам раньше, генерировали числа 0 до 9.
f = [697 770 852 941 1209 1336 1477]; freq_indices = round(f/Fs*N) + 1; dft_data = goertzel(data,freq_indices);
Постройте величину ДПФ.
stem(f,abs(dft_data)) ax = gca; ax.XTick = f; xlabel('Frequency (Hz)') title('DFT Magnitude')
Разрешите частотные составляющие шумного тона
Сгенерируйте шумный косинус с частотными составляющими на уровне 1,24 кГц, 1,26 кГц и 10 кГц. Задайте частоту дискретизации 32 кГц. Сбросьте генератор случайных чисел для восстанавливаемых результатов.
rng default Fs = 32e3; t = 0:1/Fs:2.96; x = cos(2*pi*t*10e3) + cos(2*pi*t*1.24e3) + cos(2*pi*t*1.26e3) ... + randn(size(t));
Сгенерируйте вектор частоты. Использование алгоритм Goertzel, чтобы вычислить ДПФ ограничивает область значений частот к между 1.2 и 1,3 кГц.
N = (length(x)+1)/2; f = (Fs/2)/N*(0:N-1); indxs = find(f>1.2e3 & f<1.3e3); X = goertzel(x,indxs);
Постройте среднеквадратический спектр, выраженный в децибелах.
plot(f(indxs)/1e3,mag2db(abs(X)/length(X))) title('Mean Squared Spectrum') xlabel('Frequency (kHz)') ylabel('Power (dB)') grid
Алгоритмы
Алгоритм Goertzel реализует ДПФ как рекурсивное разностное уравнение. Чтобы установить это разностное уравнение, выразите ДПФ как свертку N - вход точки, x (n), с импульсной характеристикой, где и u (n) является модульной последовательностью шага.
Z-преобразование импульсной характеристики
Прямая форма II реализаций:
Альтернативы
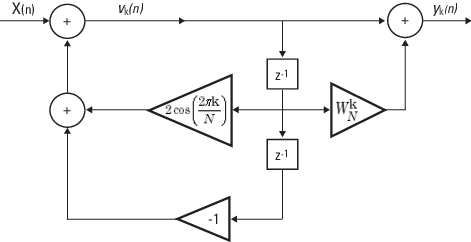
Можно также вычислить ДПФ с:
Ссылки
[1] Proakis, Джон Г. и Димитрис Г. Манолакис. Цифровая обработка сигналов: Принципы, Алгоритмы и Приложения. 3-й Выпуск. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1996, стр 480–481.
[2] Burrus, К. Сидни и Томас В. Парки. DFT/FFT и Алгоритмы Свертки: Теория и Реализация. Нью-Йорк: John Wiley & Sons, 1985.