Partial least-squares (PLS), регрессия является методом, используемым с данными, которые содержат коррелированые переменные предикторы. Этот метод создает новые переменные предикторы, известные как components, как линейные комбинации исходных переменных предикторов. PLEASE создает эти компоненты при рассмотрении наблюдаемых значений ответа, продвижении к экономной модели с надежной предсказательной силой.
Метод является чем-то вроде пересечения многофакторной линейной регрессии и анализа главных компонентов:
Многофакторная линейная регрессия находит комбинацию предикторов, которые лучше всего соответствуют ответу.
Анализ главных компонентов находит комбинации предикторов с большим отклонением, уменьшая корреляции. Метод делает нет смысла в значениях ответа.
PLEASE находит комбинации предикторов, которые имеют большую ковариацию со значениями ответа.
PLEASE поэтому комбинирует информацию об отклонениях и предикторов и ответов, также рассматривая корреляции среди них.
PLEASE совместно использует характеристики с другой регрессией и методами преобразования функции. Это похоже на гребенчатую регрессию, в которой это используется в ситуациях с коррелироваными предикторами. Это похоже на ступенчатую регрессию (или более общие методы выбора признаков), в котором это может использоваться, чтобы выбрать меньший набор условий модели. PLEASE отличается от этих методов, однако, путем преобразования исходного пробела предиктора в новый пробел компонента.
Функция Statistics and Machine Learning Toolbox™ plsregress выполняет регрессию PLEASE.
Например, рассмотрите данные по биохимическому спросу на кислород в moore.mat, дополненный шумными версиями предикторов, чтобы ввести корреляции:
load moore y = moore(:,6); % Response X0 = moore(:,1:5); % Original predictors X1 = X0+10*randn(size(X0)); % Correlated predictors X = [X0,X1];
Используйте plsregress чтобы выполнить регрессию PLEASE с тем же количеством компонентов как предикторы, затем постройте отклонение процента, объясненное в ответе как функция количества компонентов:
[XL,yl,XS,YS,beta,PCTVAR] = plsregress(X,y,10);
plot(1:10,cumsum(100*PCTVAR(2,:)),'-bo');
xlabel('Number of PLS components');
ylabel('Percent Variance Explained in y');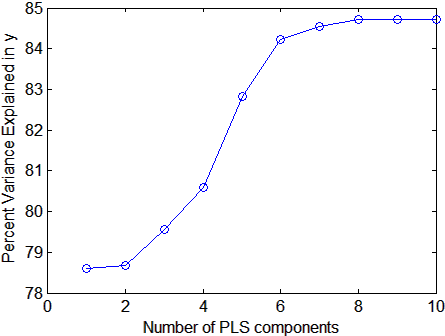
Выбор количества компонентов в модели PLEASE является критическим шагом. График дает грубую индикацию, показывая почти 80% отклонения в y объясненный первым компонентом, с целых пятью дополнительными компонентами, делающими значительные вклады.
Следующее вычисляет шестикомпонентную модель:
[XL,yl,XS,YS,beta,PCTVAR,MSE,stats] = plsregress(X,y,6); yfit = [ones(size(X,1),1) X]*beta; plot(y,yfit,'o')
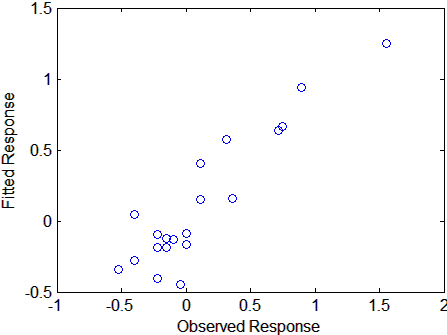
Рассеяние показывает разумную корреляцию между подходящими и наблюдаемыми ответами, и это подтверждено R 2 статистических величины:
TSS = sum((y-mean(y)).^2);
RSS = sum((y-yfit).^2);
Rsquared = 1 - RSS/TSS
Rsquared =
0.8421График весов этих десяти предикторов в каждом из этих шести компонентов показывает, что два из компонентов (последние вычисленные два) объясняют большинство отклонения в X:
plot(1:10,stats.W,'o-');
legend({'c1','c2','c3','c4','c5','c6'},'Location','NW')
xlabel('Predictor');
ylabel('Weight');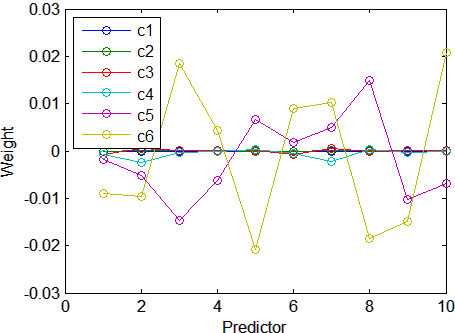
График среднеквадратических ошибок предполагает, что только два компонента могут предоставить соответствующую модель:
[axes,h1,h2] = plotyy(0:6,MSE(1,:),0:6,MSE(2,:));
set(h1,'Marker','o')
set(h2,'Marker','o')
legend('MSE Predictors','MSE Response')
xlabel('Number of Components')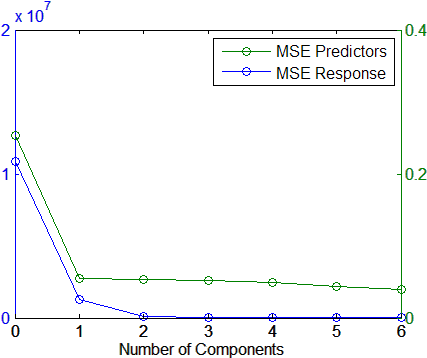
Вычисление среднеквадратических ошибок plsregress управляется дополнительным названием параметра / пары значения, задающие тип перекрестной проверки и количество повторений Монте-Карло.