generate::optimizeСгенерируйте оптимизированный код
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
generate::optimize(r)
generate::optimize(r) возвращает последовательность уравнений, представляющих “оптимизированную последовательность расчета” для входного выражения r. Каждое уравнение в последовательности соответствует присвоению подвыражения входного выражения к “временной переменной”. Общие подвыражения вычисляются только однажды, таким образом уменьшая общее количество операции.
Количество операций, а именно, сложений (или вычитания), умножение (или деления) и в конкретных вызовах функций выхода обычно ниже, чем количество таких операций входа. Это средство полезно для генерации кода.
В этом первом примере мы показываем эффекты оптимизации для простого выражения:
generate::optimize(cos(x^2) + x^2*sin(x^2) + x^4)
![]()
“Слепой” расчет входного выражения требует 7 умножения, 2 сложений и 2 вызовов функции. Оптимизированная версия вводит “временную переменную” t2 хранение подвыражения x^2 это используется для расчета конечный результат t1. Это уменьшает общую стоимость до 3 умножения, 2 сложений и 2 вызовов функции, хотя с помощью 1 дополнительного присвоения на временную переменную t2.
Здесь мы повторяем осуществление первого примера, но с массивом выражений:
generate::optimize(array(1..2, 1..2, [[x^3, x^2],[x^2, x^4]]))
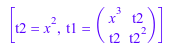
Исходный вход требует 6 умножения. Для оптимизированной версии нужны только 3 умножения и 1 дополнительное присвоение.
Мы оптимизируем список уравнений, представляющих последовательность расчета для 3 переменных tC1 C2 :
generate::optimize([t = u, C[1] = t*(u - w)^2, C[2] = 2*(u - w)^3])
![]()
Исходный расчет требует 5 умножения и 2 вычитаний. Для оптимизированной версии нужны 4 умножения и 1 вычитание.
Обратите внимание на то, что, поскольку эти примеры включают маленькие выражения, вычислительные сбережения являются небольшими. В случае очень больших выражений оптимизация может дать к значительному дивиденду.
|
Выражение, массив или список уравнений |
Список уравнений.
Много компиляторов ФОРТРАНА обеспечивают оптимизаторы. Однако они используют алгоритмы сложности O (n 2) и O (n 3), где n является размером входных выражений. Для больших объемов кода могут “повредиться” эти алгоритмы. MuPAD® обеспечивает довольно хороший скаляр (как в невекторизованном и непараллелизированном) оптимизатор, который ограничивается общей оптимизацией подвыражения и использованием двоичного файла, приводящего в действие для целочисленных степеней. Это использует хеширование выражений так, чтобы, учитывая подвыражение, это могло определить в постоянное время, если это подвыражение уже произошло. Это приводит к полному КПД, который имеет более низкую сложность а именно, O (n) т.е. линеен в размере входных выражений, которые будут оптимизированы, Следовательно полный КПД не поставился под угрозу очень большими выражениями. Это означает, что не вся возможная оптимизация сделана, но тем не менее много сокращений включая эксплуатацию некоторых симметрий возможны.
Нужно подразумевать, что “оптимизация” предназначается в смысле компиляторной оптимизации. Конечный результат редко соответствует абсолютному неприводимому минимальному количеству операций – или как в случае генерации КОДА ФОРТРАН, абсолютного минимума операций с плавающей точкой (флопс). Достижение этого предела может чрезвычайно затруднить если не невозможно специально для больших вычислительных последовательностей. Тем не менее, во многих реальных экземплярах, оптимизатор MuPAD может дать к очень полезному результату. Кроме того, MuPAD обеспечивает символьные инструменты манипуляции, такие как factor который может дать к дополнительному сокращению затрат на операцию.
Во многих случаях оптимизации, это чаще всего - вопрос того, как лучше всего создать проблему, чтобы полностью использовать каждую возможную симметрию или полезное естественное свойство данной проблемы.