Graph::depthFirstSearchДелает поиск в глубину в графике.
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Graph::depthFirstSearch(G, <StartVertex = v>)
Graph::depthFirstSearch пересечения через график через поиск в глубину. Выход показывает в первый раз идентификации, заканчивающееся время и предшественник каждой вершины. Если вершина является одной вершиной без предшественника, ее предшественником является infinity.
Graph::depthFirstSearch(G, StartVertex=v) пересечения через график через поиск в глубину, начинающий с вершины v. Выход показывает в первый раз идентификации, заканчивающееся время и предшественник каждой вершины. Если вершина является одной вершиной без предшественника, ее предшественником является infinity.
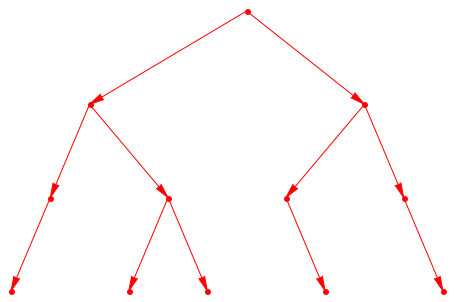
Типичное дерево создается и чертится для лучшего понимания алгоритма.
G := Graph([a, b, c, d, e, f, g, h, i, j, k, l],
[[a, b], [a, c], [b, d], [b, e], [c, f], [c, g],
[d, h], [e, i], [e, j], [f, k], [g, l]],
Directed):
plot(
Graph::plotGridGraph(G, VerticesPerLine = [12, 12, 12, 12],
VertexOrder = [
None, None, None, None, None, None,
a, None, None, None, None, None,
None, None, b, None, None, None,
None, None, None, c, None, None,
None, d, None, None, e, None,
None, f, None, None, g, None,
h, None, None, i, None, j,
None, None, k, None, None, l
]
)
)
Теперь мы вызываем Graph::depthFirstSearch узнать время начала, заканчивающиеся времена и предшественников каждой вершины:
Graph::depthFirstSearch(G)

Вершина a обнаружен сначала, затем вершина b и так далее. Таблица в середине показывает заканчивающиеся времена. h например, имеет заканчивающееся время 5, означая это вершины a, b, c, d и h самостоятельно посещались, прежде чем это было распознано тот h лист (закончивший время = время начала + 1). Правильная таблица показывает предшественника каждой вершины. backtacking от одной вершины поэтому действительно прост. a когда первая вершина, обнаруженная в ее компоненте, не может быть отслежена в обратном порядке дальше.
Что происходит теперь, если там существуют вершина, которая не имеет никакой связи ни с какой другой вершиной. Верхний пример взят, и одна вершина добавлена, не изменяя ничто больше. Затем поиск в глубину вызывается на график:
G := Graph([a, b, c, d, e, f, g, h, i, j, k, l],
[[a, b], [a, c], [b, d], [b, e], [c, f], [c, g],
[d, h], [e, i], [e, j], [f, k], [g, l]],
Directed):G2 := Graph::addVertices(G, [m]): Graph::depthFirstSearch(G2, StartVertex = [a])

Недавно вставленная вершина m не имеет никакого предшественника. Предшественник содержит поэтому значение infinity.
Если мы запускаем где-нибудь в графике, не зная корень DAG, результаты, конечно, отличаются:
G := Graph([a, b, c, d, e, f, g, h, i, j, k, l],
[[a, b], [a, c], [b, d], [b, e], [c, f], [c, g],
[d, h], [e, i], [e, j], [f, k], [g, l]],
Directed):Graph::depthFirstSearch(G, StartVertex = [c])

Предшественник c c, но если мы смотрим на график, это должен быть a. Это, тем не менее, не совсем правильно. Поиск в ширину берет данную вершину и использует это в качестве корня графика (не в вершинах!). Это объясняет также, почему следующий вызов показывает infinity предшественником к l:
Graph::depthFirstSearch(G, StartVertex = [l])

| |
|
Перечислите содержащий одну вершину. |
|
Задает вершину, с которой можно запустить глубину первый обход. |
Перечислите содержащий три таблицы. Первая таблица содержит первую идентификационную метку времени каждой вершины, второе заканчивающаяся метка времени и третье вершина-предшественник.