Graph::plotGridGraphСтроит График в размещении сетки
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Graph::plotGridGraph(G, <PointSize = n>, <VerticesPerLine = n>, <VertexOrder = [n1, …,nm]>, <SpecialVertices = [v1, …,vn]>, <SpecialEdges = [e1, …,en]>, <EdgeColor = RGB>, <SpecialEdgeColor = RGB>, <SpecialVertexColor = RGB>, <Vertex1Color = RGB>, <Vertex2Color = RGB>)
Graph::plotGridGraph(G) возвращает график:: объект Scene, в котором вершины квадратные упорядоченный (самый верхний оставленный нижнему праву). Количество вершин на строку является этажом квадратного корня количества вершин. Первая вершина чертится в RGB:: Синий и второе в RGB:: Зеленый. Все другие вершины чертятся в RGB:: Красный. Ребра чертятся в RBG:: Красный. Ширина точек предопределена с 40. Если последняя линия будет содержать только одну вершину, она будет чертиться сосредоточенная посреди линии.
Graph::plotGridGraph(G, VerticesPerLine=n) возвращает график:: объекту Scene нравится описанный выше за одним исключением. В каждой линии существует точно n вершины. Они появляются в отсортированном порядке в зависимости от их имени. Если последняя строка будет состоять только из одной вершины, этот будет сосредоточен.
Graph::plotGridGraph(G, VerticesPerLine=[v1..vn]) возвращает график:: объекту Scene нравится описанный выше за одним исключением. В линии 1 существует точно v1 вершины помещаются. В линии 2 существует v2 вершины и так далее. Последняя линия содержит vn вершины. Они появляются в отсортированном порядке в зависимости от их имени. Сумма чисел, заданных в VerticesPerLine, должна равняться количеству вершин в графике.
Graph::plotGridGraph(G, VerticesPerLine=n, VertexOrder=[v1..vn]) возвращает график:: объекту Scene нравится описанный выше за одним исключением. В каждой линии существует точно n вершины. Они появляются в отсортированном порядке в зависимости от порядка, который был задан в VertexOrder. vi может состоять из любой заданной вершины, а также замена None. Тем не менее, количество вершин в G не должен превышать количество VerticesPerLine. Если последние синхронизации строчной развертки только одна вершина, это будет сосредоточено.
Во-первых, маленький график создан и построен со значениями по умолчанию:
G := Graph([a, b, c, d], [[a, b], [b, c], [c, d], [d, a]]): plot(Graph::plotGridGraph(G))
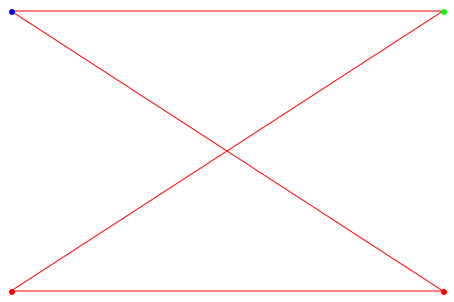
Теперь мы обмениваемся этими двумя вершинами c и d. Распоряжением, данным выше, был [a, b, c, d]:
plot(Graph::plotGridGraph(G, VertexOrder = [a, b, d, c]))

Если только одна вершина будет помещена в последнюю линию, она будет сосредоточена:
plot(Graph::plotGridGraph(G, VertexOrder = [a, b, d, c],
VerticesPerLine = 3))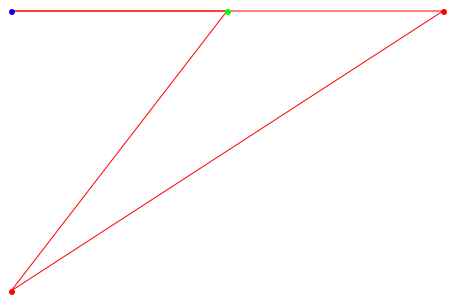
Тот же результат может быть получен путем определения Вершин на строку в частности (в этом случае, количество вершин должно быть не меньше, чем количеством вершин в графике):
plot(Graph::plotGridGraph(G, VertexOrder = [a, b, d, c],
VerticesPerLine = [3, 1]))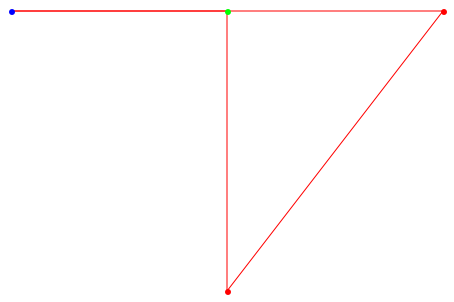
Теперь мы переходим к сути дела, почему стандартная программа графика получила имя Сетка. Замена None может использоваться каждый раз, когда место должно быть пропущено. Думайте о небольшом количестве чертежной бумаги со шкатулками. Размещение является точно тем же самым. В этом случае это состояло бы из 3 шкатулок в каждой строке. Ни один не оставляет его незаполненный, в то время как вершина из Графика чертится. Поскольку первая шкатулка пуста, первый цвет не использован, также. Вершина a то, которое помещается во вторую шкатулку, чертится, как предопределено в Vertex2Color (RGB::Green):
plot(Graph::plotGridGraph(G,
VertexOrder = [None, a, None,
b, None, c,
None, d, None],
VerticesPerLine = 3))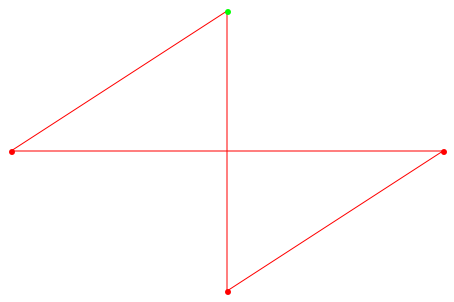
Со знанием, полученным до сих пор, возможно стать более глубоким в искусство создания объектов. Одни из самых полезных выходных параметров являются одним дерева. Таким образом График создается, чтобы использоваться в древовидном выходе:
TreeGraph := Graph([a, b, c, d, e, f, g, h, i, j, k, l],
[[a, b], [a, c], [b, d], [b, e], [c, f], [c, g],
[d, h], [e, i], [e, j], [f, k], [g, l]], Directed):Затем мы задаем специальный порядок вершины, потому что вершины не чертятся путем, они были заданы:
vOrder := [None, None, None, None, None, None, a, None, None, None, None, None, None, None, b, None, None, None, None, None, None, c, None, None, None, d, None, None, e, None, None, f, None, None, g, None, h, None, None, i, None, j, None, None, k, None, None, l ]:
Теперь пора взглянуть на то, как дерево смотрит:
plot(Graph::plotGridGraph(TreeGraph,
VerticesPerLine = 12, VertexOrder = vOrder))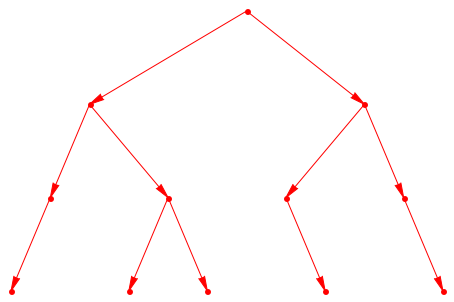
Теперь мы хотим видеть путь от вершины a к Vertexb. Для этого примера это будет дано явным образом. Для больших графиков один из shortestPath процедуры рекомендуются:
specialPath := [[a, c], [c, f], [f, k]]:
Наконец мы чертим путь в Графике и имеем хороший обзор о пути, который это берет:
plot(Graph::plotGridGraph(TreeGraph,
VerticesPerLine = 12, VertexOrder = vOrder,
SpecialEdges = specialPath, SpecialEdgeColor = RGB::Blue))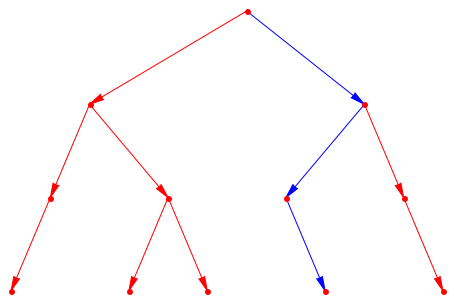
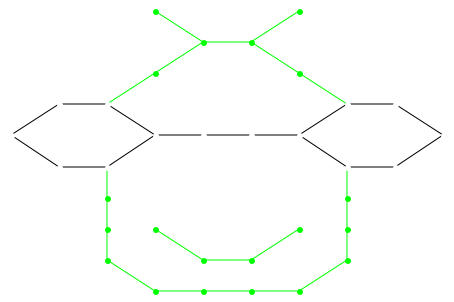
Чтобы показать, что может быть сделано с более подробными и комплексными примерами, маленькая внешняя поверхность чертится (внимательно рассмотрели ath Вершины, которые не чертятся, потому что цвет выбран к RBG:: Белый и таким образом равняется цвету фона). Additionaly, “глаза” были окрашены по-другому, таким образом, использование SpecialVertexColor мог быть представлен:
Smile := Graph([1,2,4,5,7,8,9,10,11,12,13,14,15,16,17,18,19,20,
21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36],
[[1,4],[2,5],[4,5],[7,4],[5,8],[7,10],[9,10],[10,14],[9,13],
[13,19],[19,20],[20,14],[14,15],[15,16],[16,17],[17,11],
[ 8,11],[11,12],[12,18],[18,22],[22,21],[21,17],[21,24],
[24,28],[28,32],[32,36],[36,35],[35,34],[34,33],[33,29],
[29,25],[25,23],[23,20],[26,30],[30,31],[31,27]]):
plot(
Graph::plotGridGraph(Smile, VerticesPerLine = 10,
VertexOrder = [
None,None,None, 1,None,None, 2,None,None,None,
None,None,None,None, 4, 5,None,None,None,None,
None,None,None, 7,None,None, 8,None,None,None,
None, 9, 10,None,None,None,None, 11, 12,None,
13,None,None, 14, 15, 16, 17,None,None, 18,
None, 19, 20,None,None,None,None, 21, 22,None,
None,None, 23,None,None,None,None, 24,None,None,
None,None, 25, 26,None,None, 27, 28,None,None,
None,None, 29,None, 30, 31,None, 32,None,None,
None,None,None, 33, 34, 35, 36,None,None,None],
SpecialEdges = [[13,9],[9,10],[10,14],[14,20],[20,19],[19,13],
[14,15],[15,16],[16,17],[17,21],[21,22],[22,18],[18,12],[12,11],
[11,17]],
SpecialVertices = [1,2,4,5,7,8,23,24,25,26,27,28,29,30,31,
32,33,34,35,36],
VertexColor = RGB::White,
SpecialVertexColor = RGB::Green, EdgeColor = RGB::Green,
SpecialEdgeColor = RGB::Black)
)
Следующим примером является полный график, чертивший с вершинами, упорядоченными в квадрате так, чтобы все вершины могли быть соединены в квадрате:
CG := Graph::createCompleteGraph(30):
plot(Graph::plotGridGraph(CG,
VerticesPerLine = [8, 2, 2, 2, 2, 2, 2, 2, 8],
Vertex1Color = RGB::Red, Vertex2Color = RGB::Red))
Используя значения по умолчанию в каждой линии вершины чертятся и взгляды графика, не столь “плотные” как выше одного:
plot(Graph::plotGridGraph(CG, Vertex1Color = RGB::Red,
Vertex2Color = RGB::Red))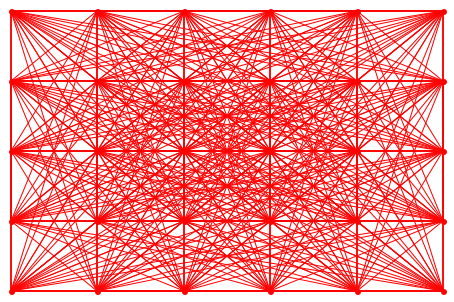
Последний пример показывает маленького бумажного змея в системе координат:
Shield := Graph([1, 2, 3, 4, 5, 6, 7, 8, 9],
[[1, 2], [1, 8], [2, 9], [8, 9], [3, 5], [4, 5],
[5, 6], [5, 7], [3, 6], [6, 7], [3, 4], [4, 7]]):
plot(Graph::plotGridGraph(Shield, Vertex1Color = RGB::White,
Vertex2Color = RGB::White, VertexColor = RGB::White,
VerticesPerLine = 7,
VertexOrder = [
1,None,None,None,None,None, 2,
None,None,None, 3,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None, 4,None, 5,None, 6,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None,None,None,None,None,
None,None,None, 7,None,None,None,
8,None,None,None,None,None, 9],
SpecialVertices = [3, 4, 5, 6, 7],
SpecialVertexColor = RGB::Blue,
SpecialEdges = [[3, 5], [4, 5], [5, 6], [5, 7],
[3, 6], [6, 7], [3, 4], [4, 7]],
SpecialEdgeColor = RGB::Blue))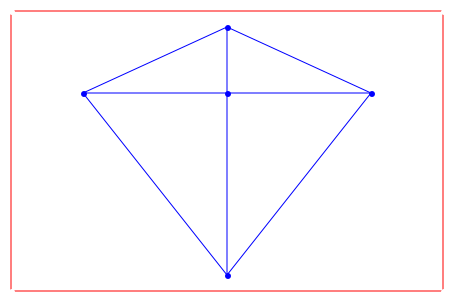
|
|
|
|
|
|
|
|
|
|
|
Задает толщину, в которой чертятся точки. Значение по умолчанию равняется 40. |
|
Если задано как один номер, это много вершин помещаются в каждую строку. Если задано как список, количество вершин на строку читается из списка. Если вершины заданы как список, количество вершин должно совпадать или с количеством вершин, заданных в графике, или, если задано, номером, заданным в |
|
Задает порядок, в который должны быть помещены вершины. Это запускается в верхнем левом углу и концах в нижнем правом углу. Количество заданных вершин должно совпадать с количеством вершин, заданных в графике или сумме вершин, заданных в VerticesPerLine. |
|
Задает набор вершин. Эта опция имеет только смысл, если используется с опцией |
|
Задает набор ребер. Эта опция имеет только смысл, если используется с опцией |
|
Задает цвет, с которым можно чертить ребра. Значением по умолчанию является RGB:: Красный |
|
Задает цвет, который будет использоваться, чтобы чертить набор заданных ребер. Эта опция имеет только смысл, если используется с опцией |
|
Задает цвет, с которым можно чертить вершины. Если эта опция задана, первые две вершины установлены в этот цвет, также. Они должны быть заданы через |
|
Задает цвет, который будет использоваться, чтобы чертить набор заданных вершин. Эта опция имеет только смысл, если используется с опцией |
|
Задает цвет, с которым можно чертить верхнюю левую (первую) вершину с (стартовая вершина). Если |
|
Задает цвет, с которым можно чертить вторую вершину с. Если |
График::.