Graph::shortestPathSingleSource
Кратчайшие пути от одной одной вершины
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
Graph::shortestPathSingleSource(G, StartVertex, <EndVertex = v>, <SearchWith = Dijkstra | Bellman>, <SearchFor = Weights | Costs>, <ReturnAsGraph>)
Описание
Graph::shortestPathSingleSource(G, StartVertex=vertex) дает длину кратчайшего пути от StartVertex к любой вершине в G.
Graph::shortestPathSingleSource(G, StartVertex=sv) возвращает таблицу со всеми путями от sv до любого другого.
Graph::shortestPathSingleSource(G, StartVertex=sv, ReturnAsGraph) возвращает table со всеми путями от sv до любого другого, потому что EndVertex должен быть приведен в порядок, чтобы получить График как возвращаемое значение.
С Graph::shortestPathSingleSource(G, StartVertex=sv, EndVertex=ev, SearchWith=Dijkstra, SearchFor=Costs) возвращает table от вершины sv к вершине ev по словам Дейкстры, который использовал затраты ребра в его алгоритме.
Примечание
Используя Дейкстру для кратчайшего пути может быть ошибочным, если график содержит отрицательные ребра.
Примечание
Если ReturnAsGraph утверждается и EndVertex не использованный, таблица возвращена, тем не менее.
Примеры
Пример 1
Маленький график, который будет использоваться в алгоритмах:
G := Graph([a, b, c, d], [[a, b], [a, c], [b, c], [c, d]],
EdgeWeights = [2, 1, 3, 2],
EdgeCosts = [1, 3, 1, 2], Directed):Теперь кратчайший путь найден по словам Белмана, использующего вес ребра, потому что никакая спецификация не была дана, и значения по умолчанию используются:
Graph::shortestPathSingleSource(G, StartVertex = [a])
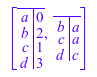
Искать график с Белманом для затрат опция SearchFor=Costs должен быть добавлен:
Graph::shortestPathSingleSource(G, StartVertex = [a],
SearchFor=Costs)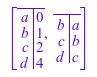
Пример 2
Теперь веса графика изменяются, так, чтобы был присвоен отрицательный вес ребра. После этого процедура называется снова с Белманом и впоследствии с Дейкстрой, чтобы сравнить результаты:
G := Graph([a, b, c, d], [[a, b], [a, c], [b, c], [c, d]],
EdgeWeights = [2, 1, 3, 2],
EdgeCosts = [1, 3, 1, 2], Directed):G := Graph::setEdgeWeights(G, Graph::getEdges(G),
[2, 1, -3, 2]):Graph::shortestPathSingleSource(G, StartVertex = [a],
SearchWith = Bellman),
Graph::shortestPathSingleSource(G, StartVertex = [a],
SearchWith = Dijkstra)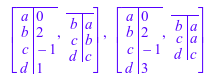
Это - типичный пример, где Дейкстра может сделать ошибку, потому что он не корректирует более ранние решения (так называемая жадная стратегия). Несмотря на то, что вершина c получает правильное значение -1, в то время d получил значение 3, вершина c все еще сохраненный значением 1. Это происходит, потому что Дейкстра сначала ищет, лучшие решения (a-> c = 1) затем пересекает далее (c-> d = 1 + 2 = 3). Несмотря на изменение значения вершины c значение для d никогда не должно изменяться снова (потому что никакой другой путь никогда не достигает его снова):
Может быть интересно видеть кратчайший путь в графике. Вот два шага, которые выполняют эту задачу:
Шаг кулака (создание графика кратчайшего пути [в этом случае с Дейкстрой]):
dijk := Graph::shortestPathSingleSource(G, StartVertex = [a],
EndVertex = [d],
SearchWith = Dijkstra,
ReturnAsGraph):Второй шаг (комбинация графиков с помощью plotGridGraph):
plot(Graph::plotGridGraph(G, VerticesPerLine = 4,
VertexOrder = [None, b, None, d, a, None, c, None],
VertexColor = RGB::Red,
SpecialEdges = Graph::getEdges(dijk),
SpecialEdgeColor = RGB::Blue))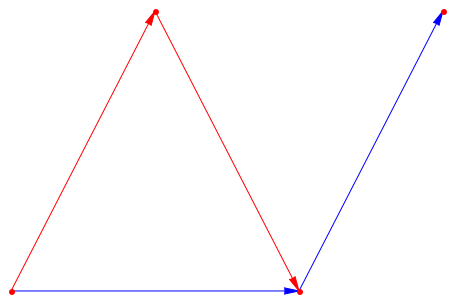
То же самое с Белманом, чтобы показать различия:
Шаг кулака (создание графика кратчайшего пути [в этом случае с Дейкстрой]):
bellm := Graph::shortestPathSingleSource(G, StartVertex = [a],
EndVertex = [d],
SearchWith = Bellman,
ReturnAsGraph):Второй шаг (комбинация графиков с помощью plotGridGraph):
plot(Graph::plotGridGraph(G, VerticesPerLine = 4,
VertexOrder = [None, b, None, d, a, None, c, None],
VertexColor = RGB::Red,
SpecialEdges = Graph::getEdges(bellm),
SpecialEdgeColor = RGB::Blue))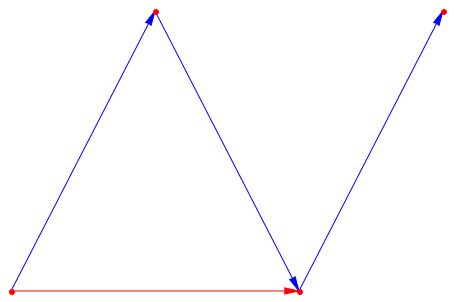
Параметры
|
График |
|
Вершина в G |
Опции
|
Задает одну вершину, к которой должен быть найден кратчайший путь. |
|
Задает алгоритм, чтобы использовать. Дейкстра может быть ошибочным, если график состоит из отрицательных ребер. Значением по умолчанию является |
|
Задает, рассматриваются ли веса графика или затраты. Значением по умолчанию является |
|
Если утверждено и EndVertex установлен, путь возвращен как График. Если утверждено и EndVertex не установлен, эта опция не использована. |
Возвращаемые значения
Или список, состоящий из двух таблиц или График. Первая таблица содержит веса или стоимость для каждой вершины и второго предшественники для каждой вершины (чтобы найти путь)
Алгоритмы
Оба, Белман и Дейкстра ожидают График без отрицательных кругов. Только Дейкстра может возвратить ошибочные результаты, когда отрицательные ребра (или веса или затраты) заданы.
Алгоритм Белмана, порожденный из: Ahuja, Magnanti, Orlin: Потоки Графика, Prentice Hall, 1 993 Раздела 5.4