polylib::primitiveElement

Примитивный элемент для башни полевых расширений

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

polylib::primitiveElement(F, G)

Описание

Для данных полевых расширений F = K (α) и G = F (β), polylib::primitiveElement(F, G) возвращает список, состоящий из простого алгебраического расширения K, который является K - изоморфный к G, символу для примитивного элемента того расширения, и изображения α и β под некоторыми зафиксировали K - изоморфизм.

Предполагается, что расширение отделимо. В противном случае это может произойти, который не останавливается алгоритм.

Примеры

Пример 1

Поскольку рациональные числа совершенны, расширения их могут всегда обрабатываться:

F := Dom::AlgebraicExtension(Dom::Rational, sqrt2^2 - 2):
G := Dom::AlgebraicExtension(F, sqrt3^2 - 3):

Теперь и мы используем polylib::primitiveElement найти примитивный элемент для G:

polylib::primitiveElement(F, G)

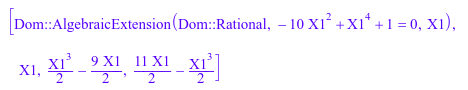
Это означает, что примитивный элемент X 1 из расширения определяется его минимальным полиномиальным X 14 - 10 X12 + 1. Последние два операнда списка являются полевыми элементами, квадраты которых равняются 2 и 3, соответственно.

Пример 2

Функция работает также на субдомены Dom::AlgebraicExtension, например, Поля Галуа.

F := Dom::GaloisField(7, 2):
G := Dom::GaloisField(F, 2):
polylib::primitiveElement(F, G)

Параметры

F

Поле создается Dom::AlgebraicExtension

G

Поле создается Dom::AlgebraicExtension с наземным полем F

Возвращаемые значения

Перечислите состоящий из четырех операндов:

  • поле H из типа Dom::AlgebraicExtension по тому же наземному полю как F;

  • идентификатор, который равняется записи H::variable;

  • объект типа H это удовлетворяет минимальному полиному для α;

  • объект типа H это удовлетворяет минимальному полиному для β.

Алгоритмы

Выбранным примитивным элементом является α + s  β, где s является положительным целым числом.

Смотрите также

Области MuPAD

Функции MuPAD

Документация Symbolic Math Toolbox
Поддержка
Для просмотра документации необходимо авторизоваться на сайте