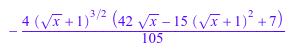Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Используйте только в Интерфейсе MuPAD Notebook. Эта функциональность не запускается в MATLAB.
Эта библиотека содержит функции для управления и решения интегралов. В настоящее время там только описаны интерфейсы для известной замены переменных методов интегрирования и интегрирования частями. Кроме того, функция для интеграции по произвольным подмножествам вещественных чисел существует. В будущих версиях будет добавлено больше интерфейсов.
Интегрирование является инверсией процесса к дифференцированию. Любой функциональный F в переменной x с
интеграл f:
f := cos(x)*exp(sin(x))
F := int(f,x)
diff(F,x)
Никакая константа не добавляется к интегралу или, другими словами, специальное постоянное интегрирование выбрано автоматически. С MuPAD® возможно определить интегралы элементарных функций, многих специальных функций и, с некоторыми ограничениями, алгебраических функций:
int(sin(x)^4*cos(x),x)
int(1/(2+cos(x)),x)
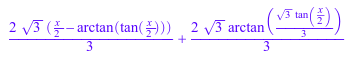
int(exp(-a*x^2),x)
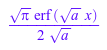
int(x^2/sqrt(1-5*x^3),x)
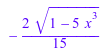
normal(simplify(diff(%,x)))
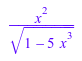
Также возможно вычислить определенные и кратные интегралы:
int(exp(-x^2)*ln(x)^2, x=0..infinity)
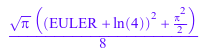
int(sin(x)*dirac(x+2)-heaviside(x+3)/x, x=1..4)
int(int(int(1, z=0..c*(1-x/a-y/b)), y=0..b*(1-x/a)), x=0..a)
Типовые приложения для правила интегрирования частями
интегралы формы
, где p (x) является полиномом. Таким образом, нужно использовать правило в способе, которым дифференцируется полином. Таким образом нужно выбрать
.
intlib::byparts(hold(int)((x-1)*cos(x),x),cos(x))
В частности с предположением
возможно вычислить много известных стандартных интегралов, как, например
.
intlib::byparts(hold(int)(arcsin(x),x),1)
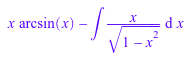
Для того, чтобы определить остающийся интеграл, можно использовать замену переменной метода
с g (x) = 1 - x 2.
F:=intlib::changevar(hold(int)(x/sqrt(1-x^2),x), t=1-x^2)
Через backsubstition в решенный интегральный F каждый получает требуемый результат.
hold(int)(arcsin(x),x) = x*arcsin(x)-subs(eval(F),t=1-x^2)
Применение замены переменной с интегратором проблематично, поскольку может произойти, что интегратор никогда не будет завершать работу. По этой причине это правило использовано в интеграторе только на определенных безопасных местах. С другой стороны, это может также привести к тому, что некоторые интегралы не могут быть решены непосредственно.
f:= sqrt(x)*sqrt(1+sqrt(x)): int(f,x)
eval(intlib::changevar(hold(int)(f,x),t=sqrt(x))) | t=sqrt(x)
