Этот раздел берет, вы через функции 1D оценки регрессии вейвлета с помощью одного из Wavelet Toolbox™ специализировали инструменты. Тулбокс предоставляет приложение Wavelet Analyzer, чтобы исследовать некоторые схемы шумоподавления одинаково или неравноценно выборочные данные.
Для примеров в этом разделе переключите дополнительный режим на симметричное дополнение, с помощью команды
dwtmode('sym')
Запустите оценку регрессии 1D инструмент.
От подсказки MATLAB® введите waveletAnalyzer.
Wavelet Analyzer появляется.
Кликните по пункту меню Regression Estimation 1-D. Дискретный аналитический инструмент вейвлета для 1D оценки регрессии появляется.
Загрузка данных.
В командной строке MATLAB ввести
load blocregdata;
В инструменте Regression Estimation 1-D выберите File> Import from Workspace. Когда диалоговое окно Import from Workspace появится, выберите blocregdata данные. Нажмите ОК, чтобы импортировать данные. Загруженные данные и обработанные данные, полученные после раскладывания, отображены.
Выберите обработанные данные.
Значение по умолчанию для количества интервалов 256 для этого примера. Войдите 64 в интервалы Nb (количество интервалов) окно редактирования или используйте ползунок, чтобы настроить значение. Новые сгруппированные данные, которые будут обработаны, появляются.
Сгруппированные данные, кажется, очень сглаживаются. Выберите 1000 из интервалов Nb, редактируют и нажимают Enter или используют ползунок. Новые данные, которые будут обработаны, появляются.
Сгруппированные данные, кажется, очень близко к исходным данным, начиная с noisbloc имеет длину 1024.
Выполните Разложение Вейвлета обработанных данных.
Выберите haar вейвлет в меню Wavelet и выбирает 5 из меню Level, и затем нажимает кнопку Decompose. После паузы для расчета инструмент отображает коэффициенты детали разложения.
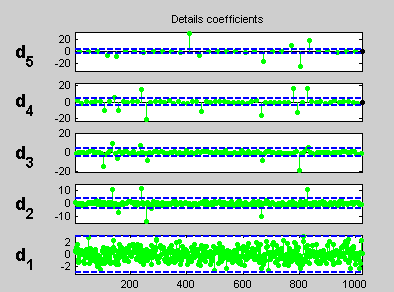
Выполните оценку регрессии.
В то время как много опций доступны для подстройки алгоритма оценки, мы примем значения по умолчанию фиксированной формы мягкая пороговая обработка и немасштабированный белый шум. Ползунки, расположенные справа от окна, управляют зависимыми порогами уровня, обозначенными желтыми пунктирными линиями, запускающимися горизонтально через графики на левой части окна.
Продолжите путем нажатия кнопки Estimate.
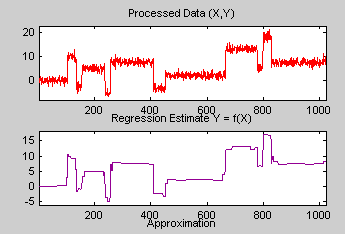
Вы видите, что процесс удалил шум и что блоки хорошо восстановлены. Оценка регрессии (в желтом) является суммой сигналов, расположенных ниже его: приближение a5 и восстановленные детали после содействующей пороговой обработки.
Можно экспериментировать с различными предопределенными стратегиями пороговой обработки путем выбора подходящих вариантов из меню, расположенного на правильной части окна или непосредственно путем перетаскивания желтых горизонтальных линий с левой кнопкой мыши.
Давайте теперь проиллюстрируем оценку регрессии с помощью приложения Wavelet Analyzer в случайным образом или нерегулярно распределенные наблюдения, фокусируясь на различиях от предыдущей ситуации.
В меню File выберите Load> опция Data for Stochastic Design Regression. Когда данные о Загрузке для диалогового окна Stochastic Design Regression появятся, выберите MAT-file ex1nsto.mat, который должен находиться в папке toolbox/wavelet/wavelet MATLAB. Кликните по кнопке OK. Этот короткий набор данных (размера 500) загружается в 1D Оценку Регрессии - Стохастический Design Tool.
Загруженные обозначенные данные (X, Y), гистограмма X, и обработанные данные, полученные после раскладывания, отображены. Гистограмма интересна, потому что значения X случайным образом распределяются. Шаг раскладывания важен, поскольку он преобразовывает проблему оценки регрессии для нерегулярно расположенного с интервалами X данных в классическую фиксированную схему проекта, для которого быстрого вейвлета преобразовывают, может использоваться.
Выберите sym4 вейвлет в меню Wavelet, выберите 5 из меню Level и войдите 125 в окно редактирования интервалов Nb. Нажмите кнопку Decompose. Инструмент отображает коэффициенты детали разложения.
В Избранном меню метода задания порога выберите элемент, Штрафуют низко и нажимают кнопку Estimate.
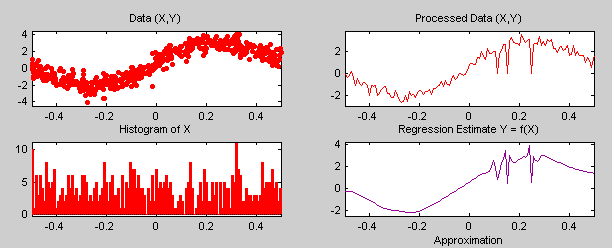
Проверяйте Overlay Estimated Function, чтобы подтвердить припадок исходных данных.
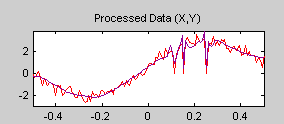
Этот инструмент позволяет вам сохранить предполагаемую функцию на диск. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете.
Чтобы избавить предполагаемую функцию от существующей оценки, используйте пункт меню File> Save Estimated Function. Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения функции. Введите имя fex1nsto. После сохранения функциональных данных к файлу fex1nsto.mat, загрузите переменные в свою рабочую область:
load fex1nsto whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
thrParams | 1x5 | 580 | cell array |
wname | 1x4 | 8 | char array |
xdata | 1x125 | 1000 | double array |
ydata | 1x125 | 1000 | double array |
Предполагаемая функция дана xdata и ydata. Длина этих векторов равна количеству интервалов, которые вы выбираете на шаге 2. Кроме того, параметры процесса оценки даны именем вейвлета, содержавшимся в wname:
wname
wname =
sym4
и зависимые пороги уровня содержатся в thrParams, который является массивом ячеек длины 5 (уровень разложения). Для i от 1 до 5, thrParams{i} содержит нижние и верхние границы интервала пороговой обработки и порогового значения (поскольку зависимые пороги интервала позволены). Для получения дополнительной информации смотрите 1D Адаптивную Пороговую обработку Коэффициентов Вейвлета в Руководстве пользователя Wavelet Toolbox.
Например, для уровня 1,
thrParams{1}
ans =
-0.4987 0.4997 1.0395
Чтобы загрузить данные для оценки регрессии, ваши данные должны быть в форме массива структур точно с двумя полями. Поля нужно назвать xdata и ydata, и должна быть та же длина.
Например, загрузите файл, содержащий данные, рассмотренные в предыдущем примере:
clear load ex1nsto whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
xdata | 1x500 | 4000 | double array |
ydata | 1x500 | 4000 | double array |
В конце этого раздела возвратите дополнительный режим, чтобы обнулить дополнение с помощью команды
dwtmode('zpd')