Шумоподавление вейвлета и непараметрическая функциональная оценка

Wavelet Toolbox™ обеспечивает много функций для оценки неизвестной функции (сигнал или изображение) в шуме. Можно использовать эти функции для сигналов denoise и как метод для непараметрической функциональной оценки.

Самая общая 1D модель для этого

s (n) = f (n) + σe (n)

где n = 0,1,2... N-1. e (n) является Гауссовыми случайными переменными, распределенными как N (0,1). Отклонение σe (n) является ^σ2.

На практике s (n) часто является сигналом дискретного времени с равными временными шагами, поврежденными аддитивным шумом, и вы пытаетесь восстановить тот сигнал.

В более общем плане можно просмотреть s (n) как N-мерный случайный вектор

$(\begin{matrix} f (0) + σ e (0) \\ f (1) + σ e (1) \\ f (2) + σ e (2) \\ . \\ . \\ . \\ f (N - 1) + σ e (N - 1) \end{matrix}) = (\begin{matrix} f (0) \\ f (1) \\ f (2) \\ . \\ . \\ . \\ f (N - 1) \end{matrix}) + (\begin{matrix} σ e (0) \\ σ e (1) \\ σ e (2) \\ . \\ . \\ . \\ σ e (N - 1) \end{matrix})$

В этом общем контексте, отношении между шумоподавлением и регрессией ясно.

Можно заменить случайный вектор N-1 N-by-M случайными матрицами, чтобы получить проблему восстановления изображения, поврежденного аддитивным шумом.

Можно получить 1D пример этой модели со следующим кодом.

load cuspamax;
y = cuspamax+0.5*randn(size(cuspamax));
plot(y); hold on;
plot(cuspamax,'r','linewidth',2);
axis tight;
legend('f(n)+\sigma e(n)','f(n)', 'Location', 'NorthWest');

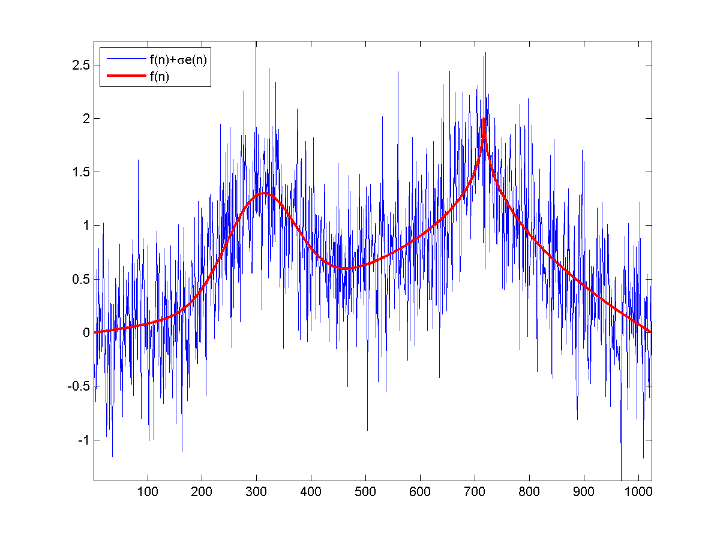
Для широкого класса функций (сигналы, изображения), которые обладают определенными свойствами гладкости, методы вейвлета оптимальны или близкие оптимальный для функционального восстановления.

А именно, метод эффективен для семейств функций f, которые имеют только несколько ненулевых коэффициентов вейвлета. Эти функции имеют разреженное представление вейвлета. Например, сглаженная функция почти везде, только с несколькими резкими изменениями, имеет такое свойство.

Общий основанный на вейвлете метод для шумоподавления и непараметрической функциональной оценки должен преобразовать данные в область вейвлета, порог коэффициенты вейвлета, и инвертировать преобразование.

Можно обобщить эти шаги как:

Разложиться
Выберите вейвлет и уровень N. Вычислите разложение вейвлета s сигнала вниз, чтобы выровнять N.
Пороговые коэффициенты детали
Для каждого уровня от 1 до N, порог коэффициенты детали.
Восстановить
Вычислите реконструкцию вейвлета с помощью исходных коэффициентов приближения уровня N и модифицированные коэффициенты детали уровней от 1 до N.

Методы шумоподавления

Wavelet Toolbox поддерживает много методов шумоподавления. Четыре метода шумоподавления реализованы в thselect. Каждый метод соответствует tptr опция в команде

thr = thselect(y,tptr)

который возвращает пороговое значение.

Опция	Метод шумоподавления
`'rigrsure'`	Выбор с помощью принципа Несмещенной оценки риска глиняной кружки (SURE)
`'sqtwolog'`	Фиксированная форма (универсальный) порог равняется $\sqrt{2 \ln (N)}$ с N длина сигнала.
`'heursure'`	Выбор с помощью смеси первых двух опций
`'minimaxi'`	Выбор с помощью минимаксного принципа

Опция 'rigrsure' использование для мягкого порогового средства оценки пороговое правило выбора на основе Объективной оценки Глиняной кружки Риска (квадратичная функция потерь). Вы получаете оценку риска для конкретного порогового значения t. Минимизация рисков в t дает выбор порогового значения.
Опция 'sqtwolog' использует фиксированный порог формы, дающий к минимаксной производительности, умноженной на маленький фактор, пропорциональный журналу (длина (s)).
Опция 'heursure' смесь двух предыдущих опций. В результате, если отношение сигнал-шум очень мало, оценка SURE является очень шумной. Таким образом, если такая ситуация обнаруживается, фиксированный порог формы используется.
Опция 'minimaxi' использует фиксированный порог, выбранный, чтобы дать к минимаксной производительности для среднеквадратичной погрешности против идеальной процедуры. Минимаксный принцип используется в статистике, чтобы спроектировать средства оценки. Поскольку сигнал denoised может ассимилироваться к средству оценки неизвестной функции регрессии, минимаксное средство оценки является опцией, которая понимает минимум, по данному набору функций, максимальной среднеквадратичной погрешности.

Следующий пример показывает методы шумоподавления для 1000 1 N (0,1) вектор. Сигнал здесь

$f (n) + e (n) e (n) ~ N (0, 1)$

с f(n) = 0.

rng default;
sig = randn(1e3,1);
thr_rigrsure = thselect(sig,'rigrsure')
thr_univthresh = thselect(sig,'sqtwolog')
thr_heursure = thselect(sig,'heursure')
thr_minimaxi = thselect(sig,'minimaxi')
histogram(sig);
h = findobj(gca,'Type','patch');
set(h,'FaceColor',[0.7 0.7 0.7],'EdgeColor','w');
hold on;
plot([thr_rigrsure thr_rigrsure], [0 300],'linewidth',2);
plot([thr_univthresh thr_univthresh], [0 300],'r','linewidth',2);
plot([thr_minimaxi thr_minimaxi], [0 300],'k','linewidth',2);
plot([-thr_rigrsure -thr_rigrsure], [0 300],'linewidth',2);
plot([-thr_univthresh -thr_univthresh], [0 300],'r','linewidth',2);
plot([-thr_minimaxi -thr_minimaxi], [0 300],'k','linewidth',2);

Для Несмещенной оценки риска глиняной кружки (SURE) и минимаксных порогов, сохраняются приблизительно 3% коэффициентов. В случае универсального порога отклоняются все значения.

Мы знаем, что содействующий вектор детали является суперпозицией коэффициентов f и коэффициентов e, и что разложение e ведет, чтобы детализировать коэффициенты, которые являются стандартными Гауссовыми белыми шумами.

После того, как вы используете thselect чтобы определить порог, вы можете порог каждый уровень a. Этот второй шаг может быть выполнен с помощью wthcoef, непосредственно обрабатывая структуру разложения вейвлета исходного s сигнала.

Мягкая или трудная пороговая обработка

Трудная и мягкая пороговая обработка является примерами правил уменьшения. После того, как вы определили свой порог, необходимо решить, как применить тот порог к данным.

Самая простая схема является трудной пороговой обработкой. Позвольте T обозначить порог и x ваши данные. Трудная пороговая обработка

$η (x) = {\begin{array}{l} x & | x | \geq T \\ 0 & | x | < T \end{array}$

Мягкая пороговая обработка

$η (x) = {\begin{array}{l} x - T & x > T \\ 0 & | x | \leq T \\ x + T & x < - T \end{array}$

Можно применить порог, использующий твердое или мягкое правило с wthresh.

y = linspace(-1,1,100);
thr = 0.4;
ythard = wthresh(y,'h',thr);
ytsoft = wthresh(y,'s',thr);
subplot(131);
plot(y); title('Original Data');
subplot(132);
plot(ythard,'*'); title('Hard Thresholding');
subplot(133);
plot(ytsoft,'*'); title('Soft Thresholding');

Контакт с немасштабированным шумовым и цветным шумом

Обычно на практике базовая модель не может использоваться непосредственно. Мы исследуем здесь опции, доступные, чтобы иметь дело с отклонениями модели в основной функции шумоподавления wdenoise.

Самое простое использование wdenoise

sd = wdenoise(s)

который возвращает denoised версию sd из исходного s сигнала полученный при помощи настроек по умолчанию для параметров включая вейвлет, метод шумоподавления и мягкую или трудную пороговую обработку. Любая из настроек по умолчанию может быть изменена:

sd = wdenoise(s,n,'DenoisingMethod',tptr,'Wavelet',wav,...
     'ThresholdRule',sorh,'NoiseEstimate',scal)

который возвращает denoised версию sd из исходного s сигнала полученное использование tptr метод шумоподавления. Другими необходимыми параметрами является sorh, scal, и wname. Параметр sorh задает пороговую обработку коэффициентов деталей разложения на уровне n из s вейвлетом под названием wav. Остающийся параметр scal должен быть задан. Это соответствует методу оценки отклонения шума в данных.

Опция	Шумовой оценочный метод
`'LevelIndependent'`	`'LevelIndependent'` оценивает отклонение шума на основе самой прекрасной шкалы (самое высокое разрешение) коэффициенты вейвлета.
`'LevelDependent'`	`'LevelDependent'` оценивает отклонение шума на основе коэффициентов вейвлета на каждом уровне разрешения.

Для более общей процедуры, wdencmp функция выполняет содействующую пороговую обработку вейвлета в целях шумоподавления и для сжатия при прямой обработке 1D и 2D данные. Это позволяет вам задавать свой собственный выбор стратегии пороговой обработки в

 xd = wdencmp(opt,x,wav,n,thr,sorh,keepapp);

где

opt = 'gbl' и thr положительное вещественное число для универсального порога.
opt = 'lvd' и thr вектор для зависимого порога уровня.
keepapp = 1 сохранить коэффициенты приближения, как ранее и
keepapp = 0 позволить содействующую пороговую обработку приближения.
x сигнал состоит в том, чтобы быть denoised и wavN, sorh эквивалентны выше.

Шумоподавление вейвлета в действии

Скрипт Open Live Script

Мы начинаем примеры 1D методов шумоподавления с первым примером, зачисленным на Донохо и Джонстона.

Пороговая обработка сигнала блоков

Сначала установите отношение сигнал-шум (SNR) и установите случайный seed.

sqrt_snr = 4;
init = 2055615866;

Сгенерируйте исходный xref сигнала и шумная версия x путем добавления стандартного Гауссова белого шума. Постройте оба сигнала.

[xref,x] = wnoise(1,11,sqrt_snr,init);
subplot(2,1,1)
plot(xref)
axis tight
title('Original Signal')
subplot(2,1,2)
plot(x)
axis tight
title('Noisy Signal')

Denoise сигнал с шумом с помощью мягкой эвристической пороговой обработки SURE на коэффициентах детали получен из разложения вейвлета x использование sym8 вейвлет. Используйте настройки по умолчанию wdenoise для остающихся параметров. Сравните с исходным сигналом.

xd = wdenoise(x,'Wavelet','sym8','DenoisingMethod','SURE','ThresholdRule','Soft');
figure
subplot(2,1,1)
plot(xref)
axis tight
title('Original Signal')
subplot(2,1,2)
plot(xd)
axis tight
title('Denoised Signal')

Только начиная с небольшого количества больших коэффициентов характеризуют исходный сигнал, метод выполняет очень хорошо.

Шумоподавление электрического сигнала

Когда вы подозреваете цветной шум, пороги должны повторно масштабироваться зависимой уровнем оценкой шума уровня. Как второй пример, давайте попробуем метод на высоко встревоженной части электрического сигнала.

Сначала загрузите электрический сигнал и выберите сегмент из него. Постройте сегмент.

load leleccum
indx = 2000:3450;
x = leleccum(indx);
figure
plot(indx,x)
axis tight
title('Original Signal')

Denoise сигнал с помощью db3 вейвлет и трехуровневое разложение вейвлета и мягкая фиксированная пороговая обработка формы. Чтобы иметь дело с цветным шумом, используйте зависимую уровнем шумовую оценку размера. Сравните с исходным сигналом.

xd = wdenoise(x,3,'Wavelet','db3',...
    'DenoisingMethod','UniversalThreshold',...
    'ThresholdRule','Soft',...
    'NoiseEstimate','LevelDependent');
figure
subplot(2,1,1)
plot(indx,x)
axis tight
title('Original Signal')
subplot(2,1,2)
plot(indx,xd)
axis tight
title('Denoised Signal')

Результат довольно хорош несмотря на неоднородность времени природы шума после и перед началом отказа датчика около времени 2410.

Расширение, чтобы отобразить шумоподавление

Скрипт Open Live Script

Метод шумоподавления, описанный для 1D случая, применяется также к изображениям и применяется хорошо к геометрическим изображениям. Прямой перевод 1D модели

$s (i, j) = f (i, j) + σ e (i, j)$

где $e$ белый Гауссов шум с модульным отклонением.

2D процедура шумоподавления имеет те же три шага и использует 2D инструменты вейвлета вместо 1D инструментов. Для порогового выбора, prod(size(s)) используется вместо length(s) если фиксированный порог формы используется.

Обратите внимание на то, что за исключением "автоматического" 1D случая шумоподавления, 2D шумоподавление и сжатие выполняются с помощью wdencmp. Чтобы проиллюстрировать 2D шумоподавление, загрузите изображение и создайте шумную версию его. В целях воспроизводимости, набор случайный seed.

init = 2055615866;
rng(init);
load woman
img = X;
imgNoisy = img + 15*randn(size(img));

Используйте ddencmp найти значения шумоподавления. В этом случае фиксированный порог формы используется с оценкой шума уровня, пороговая обработка является мягкой, и коэффициенты приближения сохранены.

[thr,sorh,keepapp] = ddencmp('den','wv',imgNoisy);
thr

thr = 107.9838

thr равно estimated_sigma*sqrt(log(prod(size(img)))).

Denoise шумное изображение с помощью глобальной пороговой опции. Отобразите результаты.

imgDenoised = wdencmp('gbl',imgNoisy,'sym4',2,thr,sorh,keepapp);
figure
colormap(pink(255))
sm = size(map,1);
subplot(2,2,1)
image(wcodemat(img,sm))
title('Original Image')
subplot(2,2,2)
image(wcodemat(imgNoisy,sm))
title('Noisy Image')
subplot(2,2,3)
image(wcodemat(imgDenoised,sm))
title('Denoised Image')

Изображение denoised соответствует хорошо оригинальному изображению.

1D отклонение вейвлета адаптивная пороговая обработка

Скрипт Open Live Script

Идея состоит в том, чтобы задать уровень уровнем зависящие от времени пороги, и затем увеличить поддержку стратегий шумоподавления обработать неустановившиеся модели шума отклонения.

Более точно модель принимает (как ранее), что наблюдение равно интересному сигналу, наложенному на шум

$s (n) = f (n) + σ e (n)$

Но шумовое отклонение может меняться в зависимости от времени. На нескольких временных интервалах существует несколько различных значений отклонения. Значения, а также интервалы неизвестны.

Давайте фокусироваться на проблеме оценки точек перехода или эквивалентно интервалов. Используемый алгоритм основан на исходной работе Марка Лэвилла об обнаружении точек перехода с помощью динамического программирования (см. [Lav99] в Ссылках).

Давайте сгенерируем сигнал из модели регрессии фиксированного проекта с двумя шумовыми точками перехода отклонения, расположенными в положениях 200 и 600. В целях воспроизводимости, набор случайный seed.

init = 2055615866;
rng(init);

x = wnoise(1,10);
bb = randn(1,length(x));
cp1 = 200;
cp2 = 600;
x = x+[bb(1:cp1),bb(cp1+1:cp2)/4,bb(cp2+1:end)];
plot(x)
title('Noisy Signal')

Цель этого примера состоит в том, чтобы восстановить эти две точки перехода с x сигнала.

Шаг 1. Восстановите сигнал с шумом путем подавления приближения. Сначала выполните одноуровневое разложение вейвлета с помощью db3 вейвлет. Затем восстановите деталь на уровне 1.

wname = 'db3';
lev = 1;
[c,l] = wavedec(x,lev,wname);
det = wrcoef('d',c,l,wname,1);
figure
plot(det)
title('Level 1 Detail')

Восстановленная деталь на уровне 1, восстановленном на данном этапе, является почти свободным сигналом. Это получает основные функции шума с точки зрения обнаружения точек перехода, если интересная часть сигнала имеет разреженное представление вейвлета. Чтобы удалить почти весь сигнал, мы заменяем самые большие значения средним значением.

Шаг 2. Чтобы удалить почти весь сигнал, замените 2% самых больших значений средним значением.

x = sort(abs(det));
v2p100 = x(fix(length(x)*0.98));
ind = find(abs(det)>v2p100);
det(ind) = mean(det);

Шаг 3. Используйте wvarchg функционируйте, чтобы оценить точки перехода следующими параметрами:

Минимальная задержка между двумя точками перехода является d = 10.
Максимальное количество точек перехода равняется 5.

[cp_est,kopt,t_est] = wvarchg(det,5)

cp_est = 1×2

   259   611

kopt = 2

t_est = 6×6

        1024           0           0           0           0           0
         612        1024           0           0           0           0
         259         611        1024           0           0           0
         198         259         611        1024           0           0
         198         235         259         611        1024           0
         198         235         260         346         611        1024

Предложены две точки перехода и три интервала. Поскольку три отклонения интервала для шума очень отличаются, программа оптимизации обнаруживает легко правильную структуру. Предполагаемые точки перехода близко к истинным точкам перехода: 200 и 600.

Шаг 4. (Необязательно) Замена предполагаемые точки перехода.

Для 2 $\leq$ i $\leq$ 6, t_est(i,1:i-1) содержит i-1 моменты точек перехода отклонения, и начиная с kopt предложенное количество точек перехода, затем

cp_est = t_est(kopt+1,1:kopt);

Можно заменить предполагаемые точки перехода путем вычисления:

for k=1:5
    cp_New = t_est(k+1,1:k)
end

cp_New = 612

cp_New = 1×2

   259   611

cp_New = 1×3

   198   259   611

cp_New = 1×4

   198   235   259   611

cp_New = 1×5

   198   235   260   346   611

Аналитические измерения шумоподавления вейвлета

Следующие измерения и настройки полезны для анализа сигналов вейвлета и изображений:

M S E — Среднеквадратичная погрешность (MSE) является нормой в квадрате различия между данными и сигналом или приближением изображений, разделенным на число элементов.
Max Error — Максимальное абсолютное отклонение в квадрате в сигнале или приближение изображений.
L2-Norm Ratio — Отношение L2-нормы в квадрате сигнала или приближения изображений к входному сигналу или изображению. Для изображений изображение изменено как вектор-столбец прежде, чем взять L2-норму
P S N R — Пиковое отношение сигнал-шум (PSNR) в децибелах. PSNR значим только для данных, закодированных в терминах битов на демонстрационные или биты на пиксель.
B P P — Отношение бит на пиксель (бит/пкс), который является коэффициентом сжатия (Аккомпанемент. Отношение) умноженный на 8, принимая один байт на пиксель (8 битов).
Comp Ratio — Коэффициент сжатия, который является числом элементов в сжатом изображении, разделенном на число элементов в оригинальном изображении, выраженном как процент.

Документация