Antenna Toolbox™ использует два типа системы координат: система прямоугольной координаты и сферическая система координат.
Antenna Toolbox использует систему прямоугольной координаты, чтобы визуализировать геометрия массивов или антенна. Тулбокс использует сферическую систему координат, чтобы визуализировать диаграммы направленности антенн.
Визуализируйте геометрию monopoleTopHat по умолчанию антенна от библиотеки антенны.
m = monopoleTopHat; show(m);
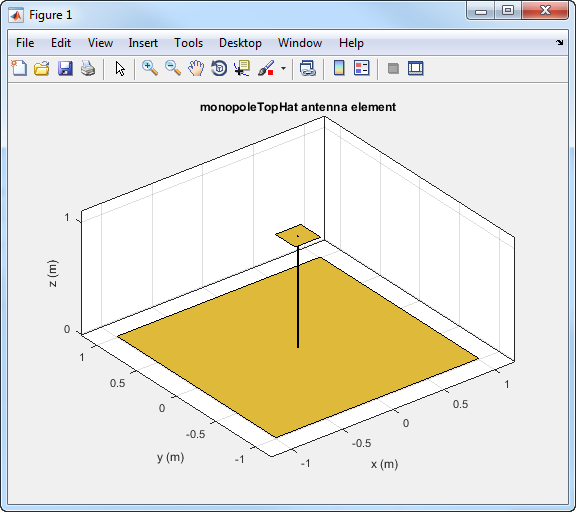
Тулбокс отображает антенну монополя цилиндра в прямоугольной или Декартовой системе координат.
Система прямоугольной координаты также под названием Декартова система координат задает положение на пробеле как упорядоченное с 3 кортежами из вещественных чисел, (x,y,z), относительно источника (0,0,0).
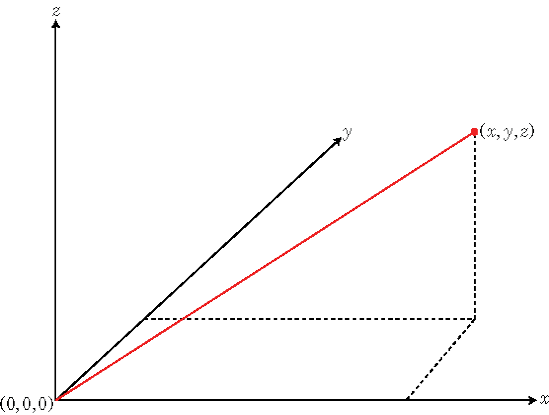
Можно просмотреть с 3 кортежами как точку на пробеле, или эквивалентно как вектор в 3D Евклидово пространстве. Когда просматривается как вектор на пробеле, оси координат являются базисными векторами, и вектор дает направление точке на пробеле от источника. Каждый вектор на пробеле исключительно определяется линейной комбинацией базисных векторов. Наиболее распространенный набор базисных векторов для 3D Евклидово пространства является стандартными модульными базисными векторами:
.
Любые три линейно независимых вектора задают основание для 3-мерного пространства. Однако Antenna Toolbox принимает, что базисные векторы, которые вы используете, являются ортогональными.
Стандартной мерой по расстоянию на пробеле является l2 норма или Евклидова норма. Евклидова норма вектора [x y z] задана:
Евклидова норма дает длину вектора, измеренного от источника как гипотенуза прямоугольного треугольника. Расстояние между двумя векторами [x0 y0 z0] и [x1 y1 z1] :
Визуализируйте диаграмму направленности monopoleTopHat по умолчанию антенна.
m = monopoleTopHat; pattern(m,75e6);
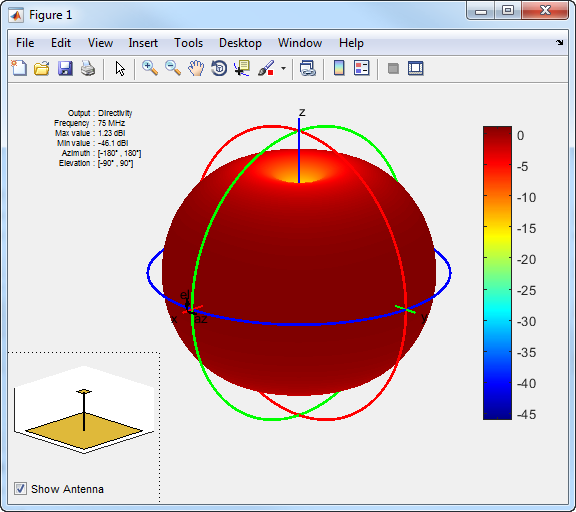
Тулбокс отображает диаграмму направленности монополя цилиндра с помощью сферической системы координат, представленной углами вертикального изменения и азимутом.
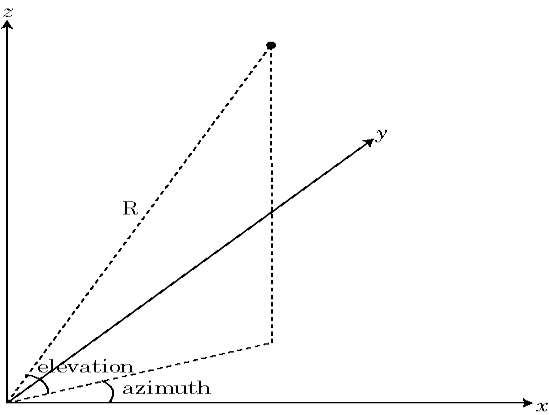
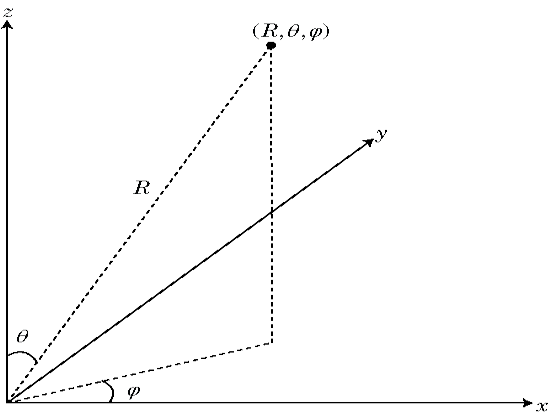
Сферическая система координат задает вектор или точку на пробеле с расстоянием R и двумя углами. Можно представлять углы в этой системе координат:
Азимут и углы вертикального изменения
Phi (Φ) и тета (θ) углы
u и координаты v
Угол азимута является углом от положительной оси X до ортогональной проекции вектора на xy плоскость, перемещающуюся в направление к оси Y. Угол азимута находится в области значений –180 и 180 градусов.
Угол вертикального изменения является углом от ортогональной проекции вектора на xy плоскость к положительной оси z к вектору. Угол вертикального изменения находится в –90 и 90 градусах.
φ угол является углом от положительной оси X до ортогональной проекции вектора на xy плоскость, перемещающуюся в направление к оси Y. Угол азимута между –180 и 180 градусами.
θ угол является углом от положительной оси z до самого вектора. θ угол находится в области значений 0 градусов и 180 градусов.
Эти углы являются альтернативой использованию азимута и углов вертикального изменения, чтобы выразить местоположение точки в сфере единичного радиуса.
Можно задать u и v в терминах φ и θ:
В терминах азимута и углов вертикального изменения, u и координаты v:
Значения u и v удовлетворяют неравенствам:
φ и θ углы в терминах u и v:
Азимут и углы вертикального изменения в терминах u и v:
Преобразуйте прямоугольные координаты в сферические координаты (азимут, el, R) использование:
Преобразуйте сферические координаты (азимут, el, R) к использованию прямоугольных координат:
где:
R является расстоянием от антенны
el и азимут являются углами вертикального изменения и азимутом
[1] Balanis, C.A. Теория антенны: анализ и проектирование. 3-й Эд. Нью-Йорк: Вайли, 2005.