Документация

Введение

Этот пример модулирует данные с помощью метода 8-PSK. Данные проходят через канал AWGN и демодулируются с помощью демодулятора 8-PSK. Системный объект калькулятора коэффициента ошибок измеряет символ и частоты ошибок по битам.

В этой системе связи, Системном объекте Модулятора PSK:

Следующая таблица указывает на отношение между бинарными представлениями во входе и фазовращателями в выходе. Второй столбец таблицы является промежуточным представлением, которое Системный объект использует в его расчетах.

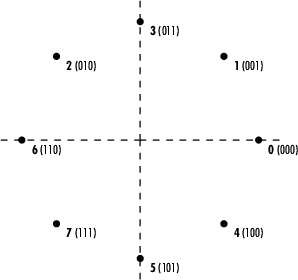
Таблица ниже видов первые два столбца из предыдущей таблицы, согласно выходным значениям. Эта сортировка делает его более ясным, что существует только различие на 1 бит между соседними символами. В следующем рисунке заметьте, что числа во втором столбце таблицы появляются в против часовой стрелки порядке.

Инициализация

Этот раздел кода инициализирует системные переменные. Это также создает и конфигурирует Системные объекты, используемые в этом примере.

Установите порядок модуляции к 8 для модуляции 8-PSK. Запустите симуляцию, пока или заданное максимальное количество битовых ошибок (maxNumErrs) или максимальное количество битов (maxNumBits) не будут достигнуты. Эта симуляция выполняет итерации по многой энергии, подведенной к долоту к шумовой степени спектральной плотности значения Eb/No.

M = 8;                    % Modulation order
SamplesPerFrame = 10000;  % Symbols processed for each iteration of the
                          % stream processing loop

% Initialize variables used to determine when to stop processing bits
maxNumErrs=100;
maxNumBits=1e8;

% Since the AWGN Channel as well as the RANDI function uses the default
% random stream, the following commands are executed so that the results
% will be repeatable, i.e. same results will be obtained for every run of
% the example. The default stream will be restored at the end of the
% example.
prevState = rng;
rng(529558);

Создайте целое число к битному конвертеру (hInt2Bit) и немного к целочисленному конвертеру (hBit2Int) Системный объект, чтобы преобразовать случайным образом сгенерированные целочисленные данные вдребезги и демодулируемые биты данных назад к целым числам

hInt2Bit = comm.IntegerToBit('BitsPerInteger',log2(M), ...
                    'OutputDataType','uint8');
hBit2Int = comm.BitToInteger('BitsPerInteger',log2(M), ...
                    'OutputDataType','uint8');

Создайте и сконфигурируйте модулятор PSK (hMod) Системный объект, чтобы сопоставить данные о двоичном входе с 8-PSK серое закодированное созвездие, а также соответствующий демодулятор PSK (hDemod) Системный объект

hMod = comm.PSKModulator('ModulationOrder',M, ...
                    'SymbolMapping','gray', ...
                    'PhaseOffset',0, ...
                    'BitInput',true);
hDemod = comm.PSKDemodulator('ModulationOrder',M, ...
                    'SymbolMapping','gray', ...
                    'PhaseOffset',0, ...
                    'BitOutput',true, ...
                    'OutputDataType','uint8', ...
                    'DecisionMethod','Hard decision');

Создайте Системный объект канала AWGN, чтобы добавить аддитивный белый Гауссов шум в модулируемый сигнал. Шумовой метод соответственно выбран так, он задает энергию, подведенную к долоту к шумовой степени спектральная плотность в потоковом цикле обработки. Поскольку модулятор PSK генерирует символы с 1 ваттом мощности, свойство степени сигнала канала AWGN также установлено в 1.

hChan = comm.AWGNChannel('NoiseMethod','Signal to noise ratio (Eb/No)', ...
                    'BitsPerSymbol',log2(M), ...
                    'SignalPower',1);

Создайте калькулятор коэффициента ошибок символа (hSymError) и немного калькулятора коэффициента ошибок (hBitError) Системный объект, чтобы сравнить демодулируемые целочисленные и битные данные с данными о первоисточнике. Это сравнение дает к статистике ошибки и битовой ошибки символа. Выход Системного объекта калькулятора коэффициента ошибок является трехэлементным вектором, содержащим расчетный коэффициент ошибок, количество ошибок, наблюдаемых, и обработанный объем данных. Симуляция использует трехэлементный вектор, сгенерированный hBitError, чтобы определить, когда остановить симуляцию.

hSymError = comm.ErrorRate;
hBitError = comm.ErrorRate;

Потоковый цикл обработки

Этот раздел кода вызывает цикл обработки, где данные являются серым закодированным, модулируемым, и демодулируемым использованием модуляция 8-PSK. Цикл симулирует систему связи для значений Eb/No в области значений 0dB к 12 дБ на шагах 2 дБ.

% For each Eb/No value, simulation stops when either the maximum number of
% errors (maxNumErrs) or the maximum number of bits (maxNumBits) processed
% by the bit error rate calculator System object is reached.
EbNoVec = 0:2:12;                             % Eb/No values to simulate
SERVec = zeros(size(EbNoVec));                % Initialize SER history
BERVec = zeros(size(EbNoVec));                % Initialize BER history
for p = 1:length(EbNoVec)
  % Reset System objects
  reset(hSymError);
  reset(hBitError);
  hChan.EbNo = EbNoVec(p);
  % Reset SER / BER for the current Eb/No value
  SER = zeros(3,1);                           % Symbol Error Rate
  BER = zeros(3,1);                           % Bit Error Rate
  while (BER(2)<maxNumErrs) && (BER(3)<maxNumBits)
    % Generate random data
    txSym = randi([0 M-1], SamplesPerFrame, 1, 'uint8');  
    txBits = step(hInt2Bit, txSym);           % Convert symbols to bits
    tx = step(hMod, txBits);                  % Modulate
    rx = step(hChan, tx);                     % Add white Gaussian noise
    rxBits = step(hDemod, rx);                % Demodulate
    rxSym = step(hBit2Int, rxBits);           % Convert bits back to symbols

    % Calculate error rate
    SER = step(hSymError, txSym, rxSym);      % Symbol Error Rate
    BER = step(hBitError, txBits, rxBits);    % Bit Error Rate
  end
  % Save history of SER and BER values
  SERVec(p) = SER(1);
  BERVec(p) = BER(1);
end

Очистка

Восстановите поток по умолчанию.

rng(prevState)

Заключения

Анализируйте данные, которые производит пример, и сравните теоретическую производительность с производительностью симуляции. Теоретическая вероятность появления ошибки символа MPSK

где erfc является дополнительной функцией ошибок, _Es/N0 является отношением энергии в символе к шумовой степени спектральная плотность, и M является количеством символов.

Чтобы определить вероятность битовой ошибки, преобразуйте вероятность появления ошибки символа, _PE, к его эквивалентной битовой ошибке. Нет никакой общей формулы для символа к преобразованию битовой ошибки. Тем не менее, верхний и нижние пределы легки установить. Фактическая вероятность битовой ошибки, _Свинец, как могут показывать, ограничена

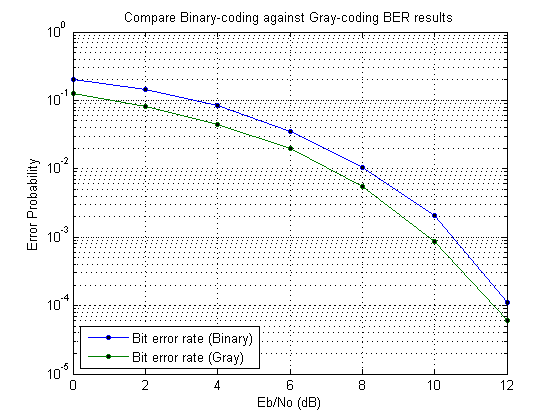
Нижний предел соответствует случаю, где символы подверглись Грэю, кодирующему. Верхний предел соответствует случаю чистого двоичного кодирования.

Следующий скрипт строит симулированные коэффициенты ошибок символа (SERVec) и частоты ошибок по битам (BERVec) вместе с теоретическими вероятностями ошибки и битовой ошибки символа.

Вычислите теоретические вероятности появления ошибки.

[theorBER, theorSER] = berawgn(EbNoVec, 'psk', M, 'nondiff');

Постройте график результатов.

figure;
semilogy(EbNoVec,SERVec,'o',   EbNoVec,BERVec,'*', ...
         EbNoVec,theorSER,'-', EbNoVec,theorBER,'-');
legend  ( 'Symbol error rate',              'Bit error rate', ...
          'Theoretical Symbol error rate',  'Theoretical Bit error rate', ...
          'Location','SouthWest');
xlabel  ( 'Eb/No (dB)' ); ylabel( 'Error Probability' );
title   ( 'Symbol and Bit Error Probability' );   grid on;

Как дальнейшее осуществление, можно сравнить Грэя, кодирующего с чистым двоичным кодированием путем изменения модулятора PSK и Системных объектов демодулятора PSK так, чтобы их параметры упорядоченного расположения созвездия были 'Двоичным файлом' вместо 'Грэя'. Установка этого свойства и повторное выполнение симуляции должны сгенерировать результаты, похожие на следующее: