Правила точности фиксированной точки для предотвращения переполнения в КИХ-фильтрах

КИХ-фильтры фиксированной точки обычно реализуются на цифровых сигнальных процессорах, FPGAs и ASICs. Фильтр фиксированной точки использует вычисления с фиксированной точкой и представлен уравнением с коэффициентами фиксированной точки. Если аккумулятор и выход КИХ-фильтра не имеют достаточных битов, чтобы представлять их данные, переполнение происходит и искажает сигнал. Используйте эти два правила, чтобы решить, что КИХ фильтрует настройки точности автоматически. Цель состоит в том, чтобы минимизировать использование ресурса (память/устройство хранения данных и элементы обработки) при предотвращении переполнения. Поскольку правила оптимизированы на основе входной точности, содействующей точности и содействующих значений, КИХ-фильтр должен иметь ненастраиваемые коэффициенты.

Правила точности задают минимум и максимальные значения КИХ-фильтра выход. Чтобы определить эти значения, выполните анализ min / макс. анализ КИХ-коэффициентов фильтра.

Выведите пределы для КИХ-фильтров

КИХ-фильтр задан:

$y [n] = \sum_{k = 0}^{N - 1} h_{k} x [n - k]$

x[n] является входным сигналом.
y[n] является выходным сигналом.
_hk является коэффициентом фильтра ^kth.
N является длиной фильтра.

Выведите пределы для КИХ-фильтров с действительным входом и действительными коэффициентами

Позвольте минимальному значению входного сигнала быть _Xmin, где _Xmin ≤ 0, и максимальное значение быть _Xmax, где _Xmax ≥ 0. Минимальный выход происходит, когда вы умножаете положительные коэффициенты на _Xmin и отрицательные коэффициенты _Xmax. Точно так же максимальный выход происходит, когда вы умножаете положительные коэффициенты на _Xmax и отрицательные коэффициенты _Xmin.

Если сумма всех положительных коэффициентов

$G^{+} = \sum_{k = 0, h_{k} > 0}^{N - 1} h_{k}$

и сумма всех отрицательных коэффициентов обозначается как

$G^{-} = \sum_{k = 0, h_{k} < 0}^{N - 1} h_{k}$

затем можно выразить минимальный выход фильтра как

$Y_{\min} = G^{+} X_{\min} + G^{-} X_{\max}$

и максимальный выход фильтра как

$Y_{\max} = G^{+} X_{\max} + G^{-} X_{\min}$

Поэтому выход фильтра находится в интервале [_Ymin, _Ymax].

Комплексные уравнения свертки фильтра

Можно задать комплексный фильтр (комплексные входные параметры и объединить коэффициенты) в терминах действительных и мнимых частей его сигналов и коэффициентов:

$\begin{array}{l} Re (y [n]) = \sum_{k = 0}^{N - 1} Re (h_{k}) Re (x [n - k]) - \sum_{k = 0}^{N - 1} Im (h_{k}) Im (x [n - k]) \\ Im (y [n]) = \sum_{k = 0}^{N - 1} Re (h_{k}) Im (x [n - k]) + \sum_{k = 0}^{N - 1} Im (h_{k}) Re (x [n - k]) \end{array}$

Комплексный фильтр разложен на четыре действительных фильтра, как изображено в схеме потока сигналов. Каждый сигнал аннотируется интервалом, обозначающим его область значений.

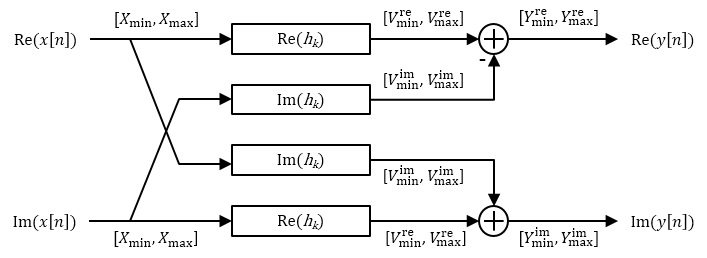
Выведите пределы для КИХ-фильтров с комплексным входом и объедините коэффициенты

Можно расширить действительный анализ min фильтра / макс. анализ, чтобы объединить фильтры. Примите, что и действительные и мнимые части входного сигнала лежат в интервале [_Xmin, _Xmax].

Комплексный фильтр содержит два экземпляра Ре фильтра (_hk). Оба фильтра имеют тот же входной диапазон и поэтому ту же выходную область значений в интервале [^Vremin, ^Vremax]. Точно так же комплексный фильтр содержит два экземпляра фильтра I am(_hk). Оба фильтра имеют ту же выходную область значений в интервале [^Vimmin, ^Vimmax].

На основе анализа min / макс. анализа действительных фильтров, можно выразить ^Vremin, ^Vremax, ^Vimmin и ^Vimmax как:

$\begin{array}{l} V_{\min}^{r e} = G_{r e}^{+} X_{\min} + G_{r e}^{-} X_{\max} \\ V_{\max}^{r e} = G_{r e}^{+} X_{\max} + G_{r e}^{-} X_{\min} \\ V_{\min}^{i m} = G_{i m}^{+} X_{\min} + G_{i m}^{-} X_{\max} \\ V_{\max}^{i m} = G_{i m}^{+} X_{\max} + G_{i m}^{-} X_{\min} \end{array}$

^G+re является суммой положительных действительных частей _hk, данного

$G_{r e}^{+} = \sum_{k = 0, Re (h_{k}) > 0}^{N - 1} Re (h_{k})$
^G-re является суммой отрицательных действительных частей _hk, данного

$G_{r e}^{-} = \sum_{k = 0, Re (h_{k}) < 0}^{N - 1} Re (h_{k})$
^G+im является суммой положительных мнимых частей _hk, данного

$G_{i m}^{+} = \sum_{k = 0, Im (h_{k}) > 0}^{N - 1} Im (h_{k})$
^G-im является суммой отрицательных мнимых частей _hk, данного

$G_{i m}^{-} = \sum_{k = 0, Im (h_{k}) < 0}^{N - 1} Im (h_{k})$

Минимальные и максимальные значения действительных и мнимых частей выхода:

$\begin{array}{l} Y_{\min}^{r e} = V_{\min}^{r e} - V_{\max}^{i m} \\ Y_{\max}^{r e} = V_{\max}^{r e} - V_{\min}^{i m} \\ Y_{\min}^{i m} = V_{\min}^{r e} + V_{\min}^{i m} \\ Y_{\max}^{i m} = V_{\max}^{r e} + V_{\max}^{i m} \end{array}$

Минимумом худшего случая и максимумом или на действительной или на мнимой части выхода дают

$\begin{array}{l} Y_{\min} = \min (Y_{\min}^{r e}, Y_{\min}^{i m}) \\ Y_{\max} = \max (Y_{\max}^{r e}, Y_{\max}^{i m}) \end{array}$

Правила точности фиксированной точки

Правила точности фиксированной точки задают выходной размер слова и дробную длину фильтра в терминах размера слова аккумулятора и дробную длину.

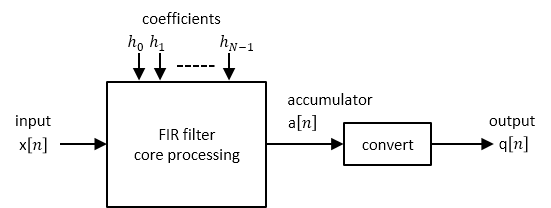
Правило аккумулятора полной точности

Примите, что вход является сигналом фиксированной точки без знака или со знаком с размером слова _Wx и дробная длина _Fx. Также примите, что коэффициенты подписываются или значения фиксированной точки без знака с дробной длиной _Fh. Можно теперь задать полную точность как настройки фиксированной точки, которые минимизируют размер слова аккумулятора при предотвращении переполнения или любой потери точности.

Длина части аккумулятора равна длине части продукта, которая является суммой входа и содействующих длин части.

$F_{a} = F_{x} + F_{h}$
Если _Ymin = 0, то аккумулятор без знака с размером слова

$W_{a} = ⌈ \log_{2} (Y_{\max} 2^{F_{a}} + 1) ⌉$

Если _Ymin> 0, то аккумулятор подписывается с размером слова

$W_{a} = ⌈ \log_{2} (\max (- Y_{\min} 2^{F_{a}}, Y_{\max} 2^{F_{a}} + 1)) ⌉ + 1$

Перекрывать оператор округляется к самому близкому целому числу к + ∞.

Выведите тот же размер слова как входное правило

Это правило устанавливает выходной размер слова совпадать с входным размером слова. Затем это настраивает дробную длину, чтобы избежать переполнения. _Wq является выходным размером слова, и _Fq является выходной длиной части.

Обрежьте аккумулятор, чтобы сделать выходной размер слова тем же самым как входной размер слова.

$W_{q} = W_{x}$

Установите выходную длину части _Fq на

$F_{q} = F_{a} - (W_{a} - W_{x})$

Многофазный Interpolators и Decimators

Можно расширить эти правила к многофазным КИХ-интерполяторам и decimators.

КИХ-интерполяторы

Обработайте каждую многофазную ветвь КИХ-интерполятора как отдельный КИХ-фильтр. Тип выходных данных КИХ-интерполятора является типом данных худшего случая всех многофазных ветвей.

КИХ Decimators

Для decimators многофазные ветви складывают при выходе. Следовательно, тип выходных данных вычисляется, как будто это был один КИХ-фильтр со всеми коэффициентами всех многофазных ветвей.

Документация

Правила точности фиксированной точки для предотвращения переполнения в КИХ-фильтрах

Выведите пределы для КИХ-фильтров

Правила точности фиксированной точки

Многофазный Interpolators и Decimators

Похожие темы

Документация DSP System Toolbox

Поддержка