До сих пор более формальное определение "урожая" и его приложение не были разработаны. Во многих ситуациях, когда поток наличности доступен, обесценивая факторы к потокам наличности, может не быть сразу очевидным. В других случаях, что релевантно, часто распространение, различие между кривыми (также известный как термин структура распространения).
Все эти вычисления требуют одного основного компонента, Казначейского пятна, урожая паритета, или передают кривую. Как правило, генерация этих кривых запускается с серии на-управляемом и выбрала не управляемые проблемы как входные параметры.
MATLAB использует эти связи, чтобы найти точечные уровни по одному, от самой короткой зрелости вперед, с помощью методов начальной загрузки. Все потоки наличности используются, чтобы создать точечную кривую, и уровни между сроками платежа (для этих купонов) интерполированы линейно.
Для рисунка того, как это работает, наблюдайте использование zbtyield (или эквивалентно zbtprice) на портфеле шести Казначейских векселей и связей.
Счета | Дата погашения | Текущая доходность |
|---|---|---|
3-месячный | 4/17/03 | 1.15 |
6-месячный | 7/17/03 | 1.18 |
| Примечания/Связи | Купон | Дата погашения | Текущая доходность |
|---|---|---|---|
2-летний | 1.750 | 12/31/04 | 1.68 |
5-летний | 3.000 | 11/15/07 | 2.97 |
10-летний | 4.000 | 11/15/12 | 4.01 |
30-летний | 5.375 | 2/15/31 | 4.92 |
Можно задать цены или урожаи к связям выше, чтобы вывести точечную кривую. Функциональный zbtyield принимает урожаи (доходность по облигациям, чтобы быть точным).
Чтобы продолжить, сначала соберите вышеупомянутую таблицу в переменную под названием Bonds. Первый столбец содержит сроки платежа, второе содержит купоны, и третье содержит notionals или номинальные стоимости связей. (Обратите внимание на то, что счета имеют нулевые купоны.)
Bonds = [datenum('04/17/2003') 0 100; datenum('07/17/2003') 0 100; datenum('12/31/2004') 0.0175 100; datenum('11/15/2007') 0.03 100; datenum('11/15/2012') 0.04 100; datenum('02/15/2031') 0.05375 100];
Затем задайте соответствующие урожаи.
Yields = [0.0115;
0.0118;
0.0168;
0.0297;
0.0401;
0.0492];
Вы теперь готовы вычислить точечную кривую для каждых из этих шести сроков платежа. Точечная кривая основана на расчетном дне от 17 января 2003.
Settle = datenum('17-Jan-2003');
[ZeroRates, CurveDates] = zbtyield(Bonds, Yields, Settle)
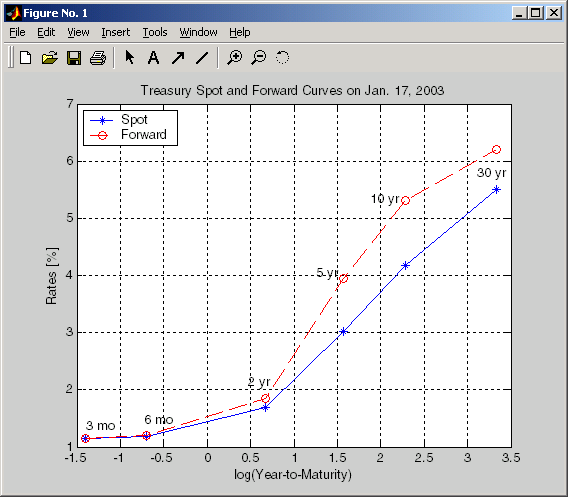
Это получает вас Казначейская кривая пятна в течение дня.
Можно вычислить прямую кривую из этой точечной кривой с zero2fwd.
[ForwardRates, CurveDates] = zero2fwd(ZeroRates, CurveDates, ... Settle)
Здесь понятие форвардных курсов относится к уровням между датами погашения, показанными выше, не к определенному периоду (передайте 3-месячные уровни, например).
Вычисление распространения между определенными, фиксированными прямыми периодами (такими как распространение Казначейского Евродоллара) требует дополнительного шага. Интерполируйте нулевые уровни (или обнулите цены, вместо этого) для соответствующих сроков платежа в даты интервала. Затем используйте интерполированные нулевые уровни, чтобы вывести форвардные курсы, и таким образом распространение Евродоллара прямые сегменты кривой по сравнению с соответствующими прямыми сегментами из Казначейских векселей.
Кроме того, множество функций кривой (включая zero2fwd) помогает стандартизировать такие вычисления. Например, путем создания обоих уровней заключенными в кавычки с ежеквартальным соединением и на фактической/360 основе, получившаяся структура распространения полностью сопоставима. Это избегает маленького несоответствия, которое происходит, непосредственно сравнивая доходность по облигациям Казначейского векселя к ежеквартальным форвардным курсам, подразумеваемым фьючерсами Евродоллара.
При представлении большего количества связей в построении кривых шум может стать фактором и, возможно, нуждается в некотором “сглаживании” (со сплайнами, например); это помогает получить более сглаженную прямую кривую.
Следующее пятно и прямые кривые создаются из 67 Казначейских облигаций. Подходящая и загруженная точечная кривая (правая нижняя фигура) отображает сопоставимую устойчивость. Прямая кривая (верхняя левая фигура) содержит значительный шум и показывает невероятную структуру форвардного курса. Шум не обязательно плохо; это могло раскрыть торговые возможности для подхода относительного значения. Все же больше сбалансированного подхода желаемо, когда загруженная прямая кривая колеблется это очень и содержит отрицательный уровень, столь же большой как-10% (не показанный в графике, потому что это находится вне пределов).
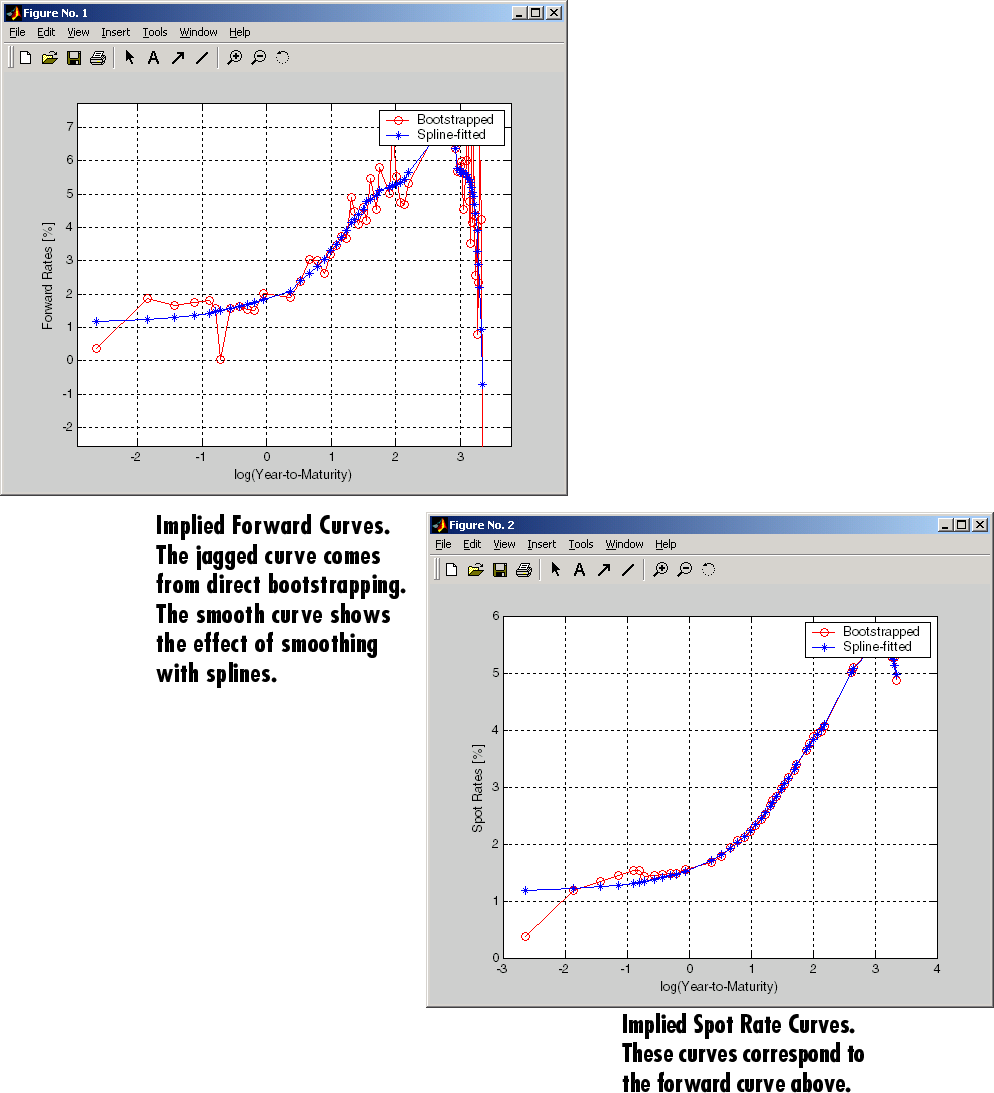
Этот пример использует termfit, функция, взятая в качестве примера, из программного обеспечения Financial Toolbox™, которое также требует использования программного обеспечения Curve Fitting Toolbox™.