Глобальная переменная по сравнению с Локальными Минимумами Используя ga

Поиск глобального минимума

Иногда цель оптимизации состоит в том, чтобы найти глобальный минимум или максимум функции — точка, где значение функции меньше или больше в любой другой точке в пространстве поиска. Однако алгоритмы оптимизации иногда возвращают локальный минимум — точка, где значение функции меньше, чем в соседних точках, но возможно больше, чем в удаленной точке в пространстве поиска. Генетический алгоритм может иногда преодолевать этот дефицит с правильными настройками.

Как пример, рассмотрите следующую функцию

$f (x) = {\begin{array}{l} - \exp (- {(\frac{x}{100})}^{2}) & для x \leq 100, \\ - \exp (- 1) + (x - 100) (x - 102) & для x > 100. \end{array}$

Следующий рисунок показывает график функции.

Код для генерации фигуры

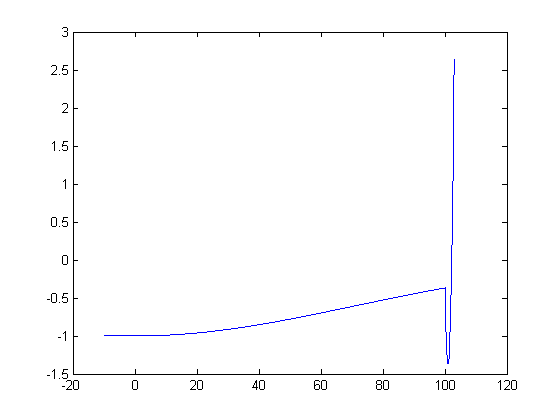
Функция имеет два локальных минимума, один в x = 0, где значение функции –1, и другой в x = 101, где значение функции –1 – 1/e. Поскольку последнее значение меньше, глобальный минимум происходит в x = 101.

Выполнение генетического алгоритма для примера

Запускать генетический алгоритм для этого примера,

Скопируйте и вставьте следующий код в новый файл в Редакторе MATLAB^®.
```
function y = two_min(x)
if x <= 100
    y = -exp(-(x/100).^2);
else
    y = -exp(-1) + (x-100)*(x-102);
end
```
Сохраните файл как two_min.m в папке на пути MATLAB.
В приложении Оптимизации,
- Установите Fitness function на @two_min.
- Установите Number of variables на 1.
- Нажмите Start.

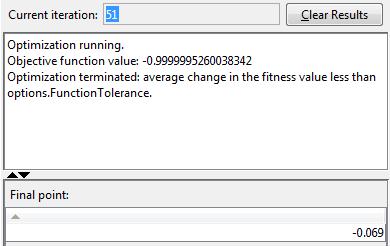
Генетический алгоритм возвращает точку очень близко к локальному минимуму в x = 0.

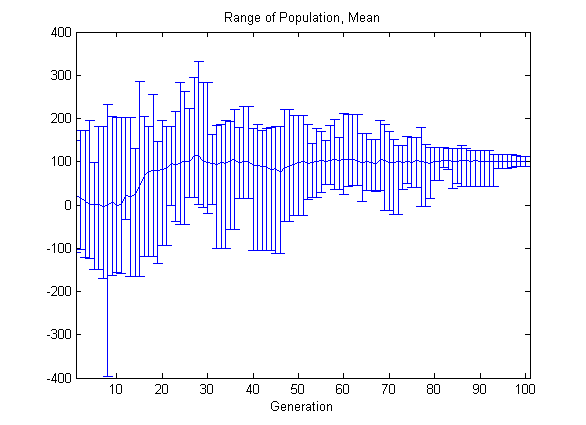
Следующий пользовательский график показывает, почему алгоритм находит локальный минимум, а не глобальный минимум. График показывает область значений индивидуумов в каждой генерации и среднем значении населения.

Код для создания фигуры

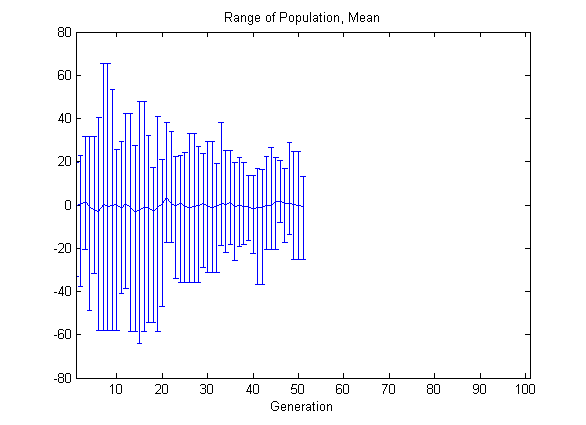
Обратите внимание на то, что все индивидуумы находятся между –70 и 70. Население никогда не исследует точки около глобального минимума в x = 101.

Запускать эту проблему с помощью функций командной строки:

options = optimoptions('ga','PlotFcn',@gaplot1drange);
x = ga(@two_min,1,[],[],[],[],[],[],[],options)

Один способ заставить генетический алгоритм исследовать более широкую область значений точек — то есть, увеличить разнообразие популяций — состоит в том, чтобы увеличить Initial range. Initial range не должен включать точку x = 101, но это должно быть достаточно большим так, чтобы алгоритм сгенерировал индивидуумов около x = 101. Установите Initial range на [-10;90] как показано в следующем рисунке.

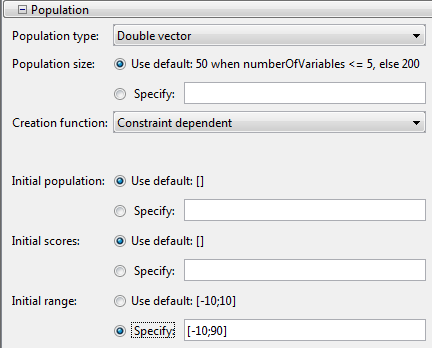
Затем нажмите Start. Генетический алгоритм возвращает точку очень близко к 101.

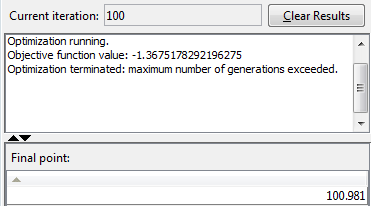
На этот раз пользовательский график показывает намного более широкую область значений индивидуумов. Существуют индивидуумы около 101 с самого начала, и среднее значение населения начинает сходиться к 101.

Запускать эту проблему с помощью функций командной строки:

options = optimoptions('ga','PlotFcn',@gaplot1drange,...
    'InitialPopulationRange',[-10;90]);
x = ga(@two_min,1,[],[],[],[],[],[],[],options)

Документация