Приложение оптимизации с lsqlin Решателем

Проблема

В этом примере показано, как использовать приложение Оптимизации, чтобы решить задачу метода наименьших квадратов с ограничениями.

Примечание

Приложение Оптимизации предупреждает, что будет удалено в будущем релизе.

Проблема в этом примере состоит в том, чтобы найти точку на плоском x ₁ + 2x2 + 4x3 = 7, который является самым близким началу координат. Самый легкий способ решить эту задачу состоит в том, чтобы минимизировать квадрат расстояния от точки x = (x ₁, x ₂, x ₃) на плоскости до начала координат, который возвращает ту же оптимальную точку как минимизация фактического расстояния. Поскольку квадрат расстояния от произвольной точки (x ₁, x ₂, x ₃) до начала координат $x_{1}^{2} + x_{2}^{2} + x_{3}^{2}$ , можно описать проблему можно следующим образом:

$\min_{x} f (x) = x_{1}^{2} + x_{2}^{2} + x_{3}^{2},$

подвергните ограничению

x ₁ + 2x2 + 4x3 = 7.

Функциональный f (x) называется целевой функцией, и x ₁ + 2x2 + 4x3 = 7 является ограничением равенства. Более сложные проблемы могут содержать другие ограничения равенства, ограничения неравенства и верхние или нижние границы ограничений.

Подготовка проблемы

Этот раздел показывает, как настроить проблему с lsqlin решатель в приложении Оптимизации.

Введите optimtool в Командном окне, чтобы открыть приложение Оптимизации.
Выберите lsqlin от выбора решателей. Используйте Interior point алгоритм.
Введите следующее, чтобы создать переменные для целевой функции:
- В поле C введите eye(3).
- В поле d введите zeros(3,1).
Поля C и d должны появиться как показано в следующем рисунке.
Введите следующее, чтобы создать переменные для ограничений равенства:
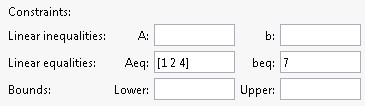
- В поле Aeq введите [1 2 4].
- В поле beq введите 7.
Поля Aeq и beq должны появиться как показано в следующем рисунке.
Нажмите кнопку Start как показано в следующем рисунке.
Когда алгоритм останавливается под Run solver and view results, следующая информация отображена:
- Значение Current iteration, когда отключенный алгоритм, который для этого примера является 1.
- Окончательное значение целевой функции, когда алгоритм остановился:
```
Objective function value: 2.333333333333334
```
- Выходное сообщение:
```
Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
```
- Конечная точка для этого примера является
```
    0.333
    0.667
    1.333
```

Документация