В этом примере показано, как вычислить весь eigenmodes с собственными значениями, меньшими, чем 100 для eigenmode проблемы УЧП
– Δu = λu
на геометрии L-образной мембраны. Граничное условие является условием Дирихле u = 0. Этот пример использует приложение PDE Modeler. Для программируемого рабочего процесса смотрите Eigenvalues и Eigenmodes L-образной Мембраны.
Чтобы решить эту задачу в приложении PDE Modeler, выполните эти шаги:
Чертите многоугольник с углами (0,0), (–1,0), (–1, –1), (1, –1), (1,1), и (0,1) при помощи pdepoly функция.
pdepoly([0,-1,-1,1,1,0],[0,0,-1,-1,1,1])
Проверяйте, что режим приложения установлен в Generic Scalar.
Используйте значение по умолчанию граничное условие Дирихле u = 0 для всех контуров. Чтобы проверить его, переключитесь на граничный режим путем выбора Boundary> Boundary Mode. Используйте Edit> Select all, чтобы выбрать все контуры. Выберите Boundary> Specify Boundary Conditions и проверьте, что граничное условие является условием Дирихле с h = 1, r = 0.
Задайте коэффициенты путем выбора PDE> PDE Specification или нажатия кнопки PDE на панели инструментов. Это - задача о собственных значениях, так выберите тип Eigenmodes УЧП. Общий УЧП собственного значения описан . Таким образом, для этой проблемы, используйте коэффициенты по умолчанию c = 1, a = 0, и d = 1.
Задайте максимальный размер ребра для mesh путем выбора Mesh> Parameters. Установите максимальное значение размера ребра к 0,05.
Инициализируйте mesh путем выбора Mesh> Initialize Mesh.
Укажите диапазон собственного значения путем выбора Solve> Parameters. В получившемся диалоговом окне используйте область значений собственного значения по умолчанию [0 100].
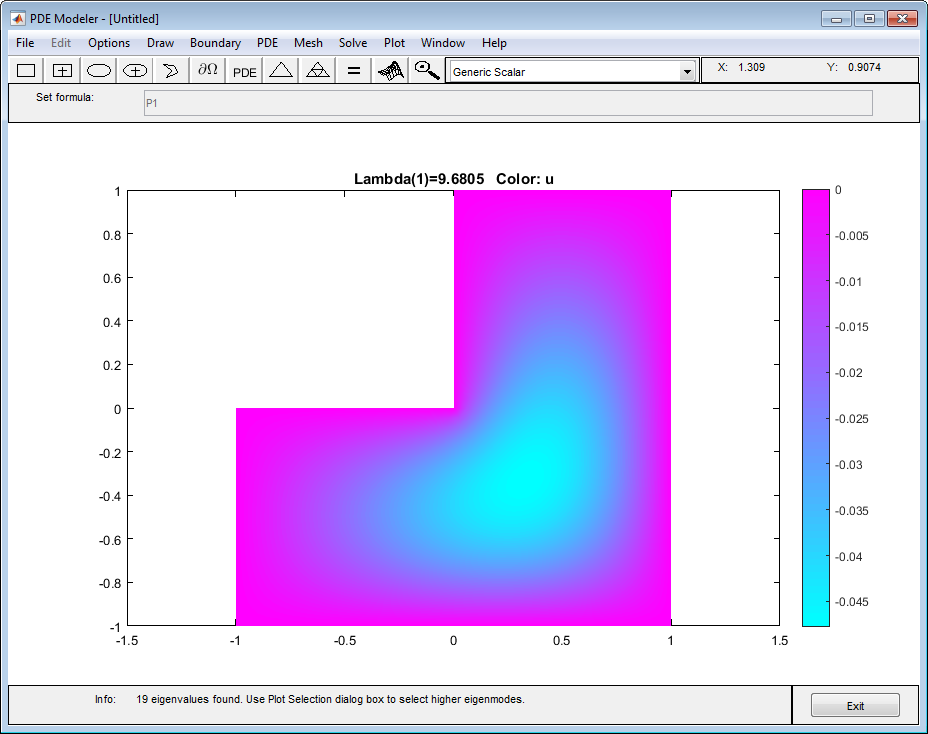
Решите УЧП путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов. По умолчанию приложение строит первую собственную функцию.
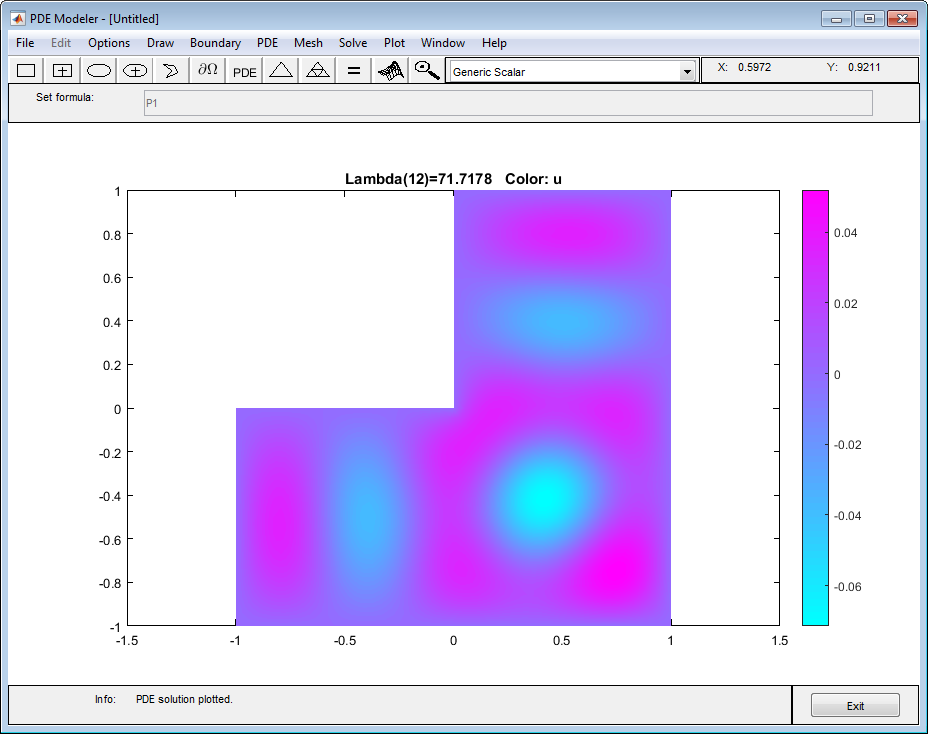
Постройте другие собственные функции путем выбора Plot> Parameters и затем выбора соответствующего собственного значения из выпадающего списка в нижней части диалогового окна. Например, постройте пятую собственную функцию в заданной области.