Решите 3-D параболическую задачу УЧП путем сокращения проблемы до 2D преобразования координаты использования. Этот пример использует приложение PDE Modeler. Для решения командной строки смотрите Распределение Тепла в Круговом Цилиндрическом Стержне.
Рассмотрите цилиндрический радиоактивный стержень. Тепло постоянно добавляется в левом конце стержня, в то время как правильный конец сохранен при постоянной температуре. Во внешней границе теплом обмениваются со средой переводом. В то же время тепло однородно производится в целом стержне из-за радиоактивных процессов. Предположение, что начальная температура является нулем, приводит к следующему уравнению:
Здесь, ρ, C и k являются плотностью, тепловой способностью и теплопроводностью материала, u является температурой, и q является теплом, выработанным в стержне.
Поскольку проблема осесимметрична, удобно написать это уравнение в системе цилиндрической координаты.
Здесь r, θ и z являются тремя координатными переменными цилиндрической системы. Поскольку проблема осесимметрична, .
Это - цилиндрическая проблема, и Partial Differential Equation Toolbox™ требует, чтобы уравнения были в Декартовых координатах. Чтобы преобразовать уравнение к Декартовым координатам, сначала умножьте обе стороны уравнения r:
Затем задайте r как y и z как x:
В данном примере используйте эти параметры:
Плотность, ρ = 7 800 кг/м3
Тепловая способность, C = 500 Вт · s/kg · ºC
Теплопроводность, k = 40 W/mºC
Радиоактивный источник тепла, q = 20000 W/m3
Температура в правильном конце, T_right = 100 ºC
Нагрейте поток в левом конце, HF_left = 5000 W/m2
Окружающая температура во внешней границе, T_outer = 100 ºC
Коэффициент теплопередачи, h_outer = 50 W/m2 · ºC
Чтобы решить эту задачу в приложении PDE Modeler, выполните эти шаги:
Смоделируйте стержень как прямоугольник с углами в (-1.5,0), (1.5,0), (1.5 0.2), и (-1.5 0.2). Здесь, x - ось представляет направление z и y - ось представляет направление r.
pderect([-1.5,1.5,0,0.2])
Задайте граничные условия. Для этого дважды кликните контуры, чтобы открыть диалоговое окно Boundary Condition. Приложение PDE Modeler требует граничных условий в конкретной форме. Таким образом Неймановы граничные условия должны быть в форме , и граничные условия Дирихле должны быть в форме h u = r. Кроме того, потому что обе стороны уравнения умножаются на r = y, умножают коэффициенты для граничных условий y.
Для левого конца используйте Нейманово условие . Задайте g = 5000*y и q = 0.
Для правильного конца используйте условие Дирихле u = T_right = 100. Задайте h = 1 и r = 100.
Для внешней границы используйте Нейманово условие . Задайте g = 50*y*100 и q = 50*y.
Цилиндрический r оси = 0 не является контуром в исходной проблеме, но в 2D обработке это стало той. Используйте искусственное Нейманово граничное условие в оси, . Задайте g = 0 и q = 0.
Задайте коэффициенты путем выбора PDE> PDE Specification или нажмите кнопку PDE на панели инструментов. Нагрейтесь уравнение является параболическим уравнением, так выберите тип Parabolic УЧП. Поскольку обе стороны уравнения умножаются на r = y, умножают коэффициенты на y и вводят следующие значения: c = 40*y, a = 0, f = 20000*y, и d = 7800*500*y.
Инициализируйте mesh путем выбора Mesh> Initialize Mesh.
Установите начальное значение к 0, время решения к 20 000 секунд, и вычисляйте решение каждые 100 секунд. Для этого выберите Solve> Parameters. В диалоговом окне Solve Parameters, время набора к 0:100:20000, и u (t 0) к 0.
Решите уравнение путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов.
Постройте решение, с помощью цвета и контурного графика. Для этого выберите Plot> Parameters и выберите цвет и контурные графики в получившемся диалоговом окне.
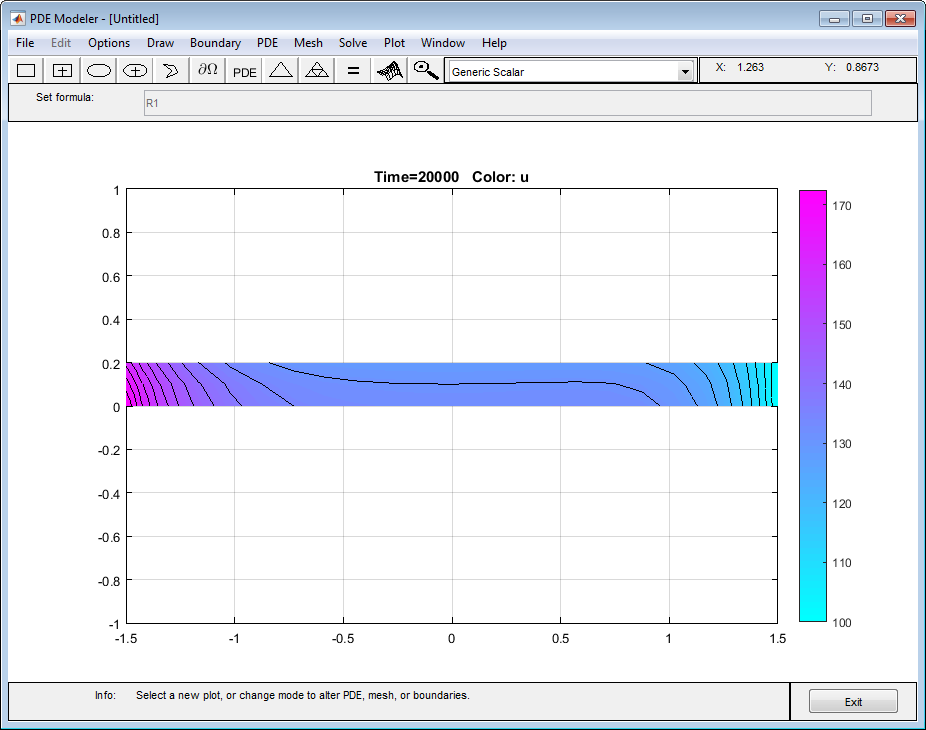
Можно исследовать решение путем варьирования параметров модели и графического вывода результатов. Например, вы можете:
Покажите решение, когда u не будет зависеть вовремя, то есть, решение для устойчивого состояния. Для этого откройте диалоговое окно PDE Specification и измените тип УЧП в Elliptic. Получившееся решение для устойчивого состояния находится в близком соглашении с переходным решением в 20 000 секунд.
Покажите решение для устойчивого состояния, не охлаждаясь на внешней границе: коэффициент теплопередачи является нулем. Для этого установите Нейманово граничное условие во внешней границе (главная сторона прямоугольника) к g = 0 и q = 0. Получившийся график показывает, что температура повышается до больше чем 2 500 на левом конце стержня.