Моделирование движения в поэтапных системах массивов

Поддержка моделирования движения

Критический компонент в поэтапных системных приложениях массивов является способностью смоделировать движение на пробеле. Такое моделирование включает движение массивов, целей и источников интерференции. Для удобства можно проигнорировать различие между этими объектами и коллективно смоделировать движение платформы.

Расширенные тела могут подвергнуться и поступательному и вращательному движению на пробеле. Моделирование поддержек программного обеспечения Phased Array System Toolbox™ поступательного движения.

Моделирование поступательного движения платформы требует спецификации радиус-вектора и вектора скорости. Спецификация радиус-вектора подразумевает систему координат. В Phased Array System Toolbox положение платформы и скорость заданы в Глобальной системе координат. Можно думать о позиции платформы вектора смещения от глобального источника или как координаты точки относительно глобального источника.

Позвольте _r0 обозначить, что радиус-вектор во время 0 и v обозначает вектор скорости. Радиус-вектор платформы как функция времени, r(t):

$r (t) = r_{0} + v t$

Следующая фигура изображает векторную интерпретацию поступательного движения.

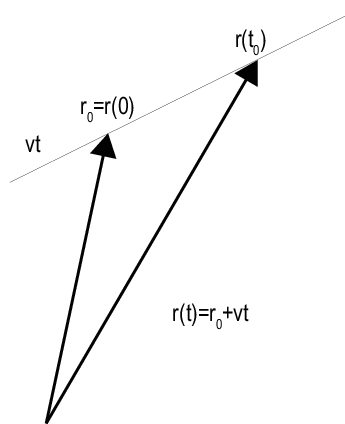
Когда платформа представляет элемент датчика или массив, важно знать ориентацию элемента или осей локальной координаты массивов. Например, ориентация осей локальной координаты необходима, чтобы извлечь информацию об угле из инцидентных форм волны. Смотрите Системы Глобальной и Локальной координаты для описания систем глобальной и локальной координаты в программном обеспечении. Наконец, для платформ с различной скоростью, необходимо смочь обновить вектор скорости в зависимости от времени.

Можно смоделировать положение платформы, скорость и локальную ориентацию осей с phased.Platform объект.

Движение платформы с постоянной скоростью

Скрипт Open Live Script

При начале с простого примера смоделируйте движение платформы более чем десять временных шагов. Чтобы определить временной шаг, примите, что у вас есть импульсный передатчик с импульсной частотой повторения (PRF) 1 килогерца. Соответственно, временной интервал между каждым импульсом является 1 миллисекундой. Установите временной шаг, равный импульсному интервалу повторения.

PRF = 1e3;
Tstep = 1/PRF;
Nsteps = 10;

Затем создайте объект платформы определение исходного положения платформы и скорости. Примите, что исходное положение платформы в 100 метрах от источника в (60,80,0). Примите, что скорость составляет приблизительно 30 метров в секунду (m/s) с постоянным вектором скорости, данным (15,25.98,0).

platform = phased.Platform('InitialPosition',[60;80;0],'Velocity',[15;25.98;0]);

Ориентация осей локальной координаты платформы является значением InitialOrientationAxes свойство. Можно просмотреть значение этого свойства путем ввода hplat.InitialOrientationAxes в командной строке MATLAB™. Поскольку InitialOrientationAxes свойство не задано в конструкции phased.Platform Система object™, свойство присвоено его значение по умолчанию [1 0 0;0 1 0;0 0 1]. Используйте step метод, чтобы симулировать поступательное движение платформы.

initialPos = platform.InitialPosition;
for k = 1:Nsteps
    pos = platform(Tstep);
end
finalPos = pos + platform.Velocity*Tstep;
distTravel = norm(finalPos - initialPos)

distTravel = 0.3000

step метод возвращает текущее положение платформы и затем обновляет положение платформы на основе временного шага и скорости. Эквивалентно, в первый раз вы вызываете step метод, выход является положением платформы в t = 0.

Вспомните, что платформа перемещается с постоянной скоростью приблизительно 30 м/с. Общее истекшее время составляет 0,01 секунды. Вызов step метод возвращает текущее положение платформы и затем обновляет то положение. Соответственно, вы ожидаете, что конечное положение будет отличаться от исходного положения на 0,30 метра. Подтвердите это различие путем исследования значения distTravel.

Движение платформы с изменяющейся скоростью

Скрипт Open Live Script

Большинство платформ в поэтапных приложениях массивов не перемещается с постоянной скоростью. Если временной интервал, описанный количеством временных шагов, мал относительно скорости платформы, можно часто аппроксимировать скорость как постоянную. Однако существуют ситуации, где необходимо обновлять скорость платформы в зависимости от времени. Можно сделать так с phased.Platform Система Object™, потому что Velocity свойство является настраиваемым.

Этот пример моделирует цель первоначально в покое. Начальный вектор скорости (0,0,0). Примите, что временной шаг является 1 миллисекундой. После 500 миллисекунд платформа начинает перемещаться со скоростью приблизительно 10 м/с. Вектор скорости (7.07,7.07,0). Платформа продолжается при этой скорости еще для 500 миллисекунд.

Tstep = 1e-3;
Nsteps = 1/Tstep;
platform = phased.Platform('InitialPosition',[100;100;0]);
for k = 1:Nsteps/2
    [tgtpos,tgtvel] = platform(Tstep);
end
platform.Velocity = [7.07; 7.07; 0];
for k = Nsteps/2+1:Nsteps
    [tgtpos,tgtvel] = platform(Tstep);
end

Отследите область значений, и угол изменяется между платформами

Скрипт Open Live Script

Этот пример использует phased.Platform Система object™, чтобы смоделировать изменение в области значений между стационарным радаром и движущейся целью. Радар расположен в (1000,1000,0) и имеет скорость (0,0,0). Цель имеет исходное положение (5000,8000,0) и перемещается с постоянной скоростью (? 30? 45,0). Импульсная частота повторения (PRF) составляет 1 кГц. Примите, что радар испускает десять импульсов.

PRF = 1e3;
Tstep = 1/PRF;
radar = phased.Platform('InitialPosition',[1000;1000;0]);
target = phased.Platform('InitialPosition',[5000;8000;0],...
    'Velocity',[-30;-45;0]);

Вычислите начальный целевой диапазон и угол.

[initRng, initAng] = rangeangle(target.InitialPosition,radar.InitialPosition);

Вычислите относительную радиальную скорость.

v = radialspeed(target.InitialPosition,target.Velocity,...
    radar.InitialPosition);

Симулируйте целевое движение.

Npulses = 10;
for num = 1:Npulses
    tgtpos = target(Tstep);
end

Вычислите последнее целевое положение.

tgtpos = tgtpos + target.Velocity*Tstep;

Вычислите итоговый целевой диапазон и угол.

[finalRng,finalAng] = rangeangle(tgtpos,radar.InitialPosition);
deltaRng = finalRng - initRng

deltaRng = -0.5396

Постоянная скорость цели составляет приблизительно 54 м/с. Общее истекшее время составляет 0,01 секунды. Область значений между целью и радаром должна уменьшиться приблизительно на 54 сантиметра. Сравните начальную область значений цели, initRng, к итоговой области значений, finalRng, подтвердить, что это уменьшение происходит.

Документация