Pipe (TL)

Закрытый кабелепровод для транспорта жидкости между тепловыми жидкими компонентами

Библиотека:
Simscape / Жидкости / Тепловая Жидкость / Pipes & Fittings

Описание

Блок Pipe (TL) моделирует поток тепловой жидкости через закрытый кабелепровод, такой как трубопровод. Стенка кабелепровода может быть твердой или гибкой, последний случай, допуская расширение и сокращение в радиальном направлении, как совместимый шланг или, в науках о жизни, артерия может. Тепловые гидравлические порты могут быть при различных вертикальных изменениях, и вертикальным расстоянием между ними можно управлять (через физический сигнал), например, чтобы получить банковское дело хода изменения самолета.

Падение давления через трубопровод определяется как функция трения между жидкостью и трубопроводом и повышения или понижения высоты между портами. Для расширенной точности в моделях с быстрыми изменениями потока (такими как сопоставленные с эффектом гидравлического удара) блок может быть сконфигурирован, чтобы получить динамическую сжимаемость жидкости и ее инерции. Обратите внимание на то, что такие эффекты могут уменьшить скорость симуляции и должны использоваться только при необходимости.

Изменение температуры через трубопровод определяется из энергетических обменов между трубопроводом и остатком от модели. Эти обмены включают приписанных адвекции и проводимости внутренней энергии через тепловые гидравлические порты (A и B) и к конвекции тепла через тепловой порт (H). Вычисление получает также различия в вертикальном изменении и статическом давлении, установленном в процессе моделирования между тепловыми гидравлическими портами.

Если тепловая жидкость обработана как сжимаемая, трубопровод может быть дискретизирован в равные сегменты, каждый содержащий фрагмент общего объема жидкости. Внутренние объемы жидкости, такие как они служат особому назначению в тепловой жидкой области: они обеспечивают вычислительные узлы, в которых можно вычислить доменные и переменные компонента в процессе моделирования. Чем больше количество сегментов трубопровода, тем более прекрасный дискретизация и более точное результаты симуляции (хотя в уменьшаемой скорости симуляции).

Блокируйте варианты

Чтобы получить повышение вертикального изменения порта, блок обеспечивает два варианта. Опция по умолчанию обрабатывает это количество как константу (заданный через параметры блоков Elevation gain from port A to port B). Альтернативный вариант обрабатывает его как переменную (управляемый портом El физического сигнала). Чтобы изменить варианты блока, щелкните правой кнопкой по блоку и, в его контекстно-зависимом меню, выберите Simscape + Block Choices. Кликните по желаемому варианту: Constant elevation или Variable elevation.

Параметризация

Чтобы смоделировать потери на трение с помощью данных, подходящих лучше всего для конкретного приложения, блок обеспечивает массив параметризации трения. Некоторые основаны на аналитических выражениях, требующих только небольшого количества эмпирических констант; корреляция Haaland является одним таким выражением. Другие основаны на табличных данных, связывающих различные количества интереса — коэффициент трения Дарси против числа Рейнольдса, например, или номинальный перепад давления к номинальному массовому расходу жидкости.

Аналитическая и сведенная в таблицу параметризация обеспечивается также для теплопередачи между тепловой жидкостью и стенкой трубопровода. Параметризация Analytical включает тех на основе эмпирических корреляций Гниелинского и Диттус-Боелтера. Сведенная в таблицу параметризация включает тех на основе данных, связывающих коэффициент Колборна с числом Рейнольдса, номер Nusselt Рейнольдсу и числам Прандтля или номинальному температурному дифференциалу к номинальному массовому расходу жидкости.

Дискретизация трубопровода

Если трубопровод сегментируется так, чтобы он содержал больше чем один объем жидкости, то общая масса, импульс и энергетическое накопление в его промежутке определяются как суммы по объемам, что трубопровод содержит. Сегментированные трубопроводы обработаны как блоки меньших трубопроводов, каждый трубопровод, сопоставленный с отдельным экземпляром этого блока (каждый блок, сконфигурированный, чтобы обеспечить один объем жидкости). Вычисления, описанные для этого блока, применяются к трубопроводу с одним объемом жидкости.

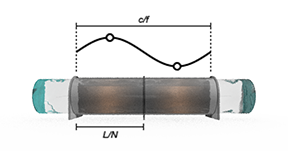
Соответствующее количество сегментов трубопровода, чтобы использовать в модели зависит частично от масштабов времени, по которым температура и воздействия давления имеют тенденцию распространять через трубопровод. Волны давления перемещаются самое быстрое (они делают так на скорости звука в жидкости), и часто ограничивающий фактор уровня, чтобы рассмотреть. В соответствии с теоремой отсчетов Найквиста, для того, чтобы получить элементарное синусоидальное воздействие, по крайней мере два вычислительных узла — и поэтому передать сегменты по каналу — должно быть доступно для выборки в одной длине волны:

$\frac{c}{f} = 2 \frac{L}{N},$

где c является скоростью звука, f является частотой воздействия (в Герц), L является общей длиной трубопровода, и N является количеством сегментов трубопровода. Левая сторона представляет длину волны воздействия давления и правой стороны длина сегмента трубопровода — каждый предоставляющий один вычислительный узел трубопроводу. Чтобы получить те воздействия давления с частотами до максимального f _Max, количество сегментов в трубопроводе должно поэтому быть, по крайней мере:

$N = 2 L \frac{f}{c},$

Используйте это выражение в качестве свободной инструкции в установке дискретизации трубопровода. Другие ограничения моделирования могут включить в решение о том, сколько сегментов трубопровода, чтобы использовать и даже о том, как смоделировать их. Больше сегментов трубопровода может требоваться, например, правильно задать тепловое граничное условие вдоль трубопровода; сегменты трубопровода находятся в таком случае, более адекватно смоделированном явным образом, с помощью отдельного блока Pipe (TL) в каждом (и используя его тепловой порт, чтобы установить тепловое граничное условие).

Используйте регистрацию данных Simscape, чтобы получить доступ к тепловым жидким свойствам и состояниям в различных узлах, соответствующих сегментам трубопровода.

Баланс массы

Тепловой жидкий поток вводит и выходит из трубопровода через тепловые гидравлические порты A и B. В случае по умолчанию твердого трубопровода фиксируется объем жидкости, содержавшей между этими портами. Если тепловая жидкость обработана как несжимаемая, ее плотность (в данных условиях работы) фиксируется также, и ее масса в трубопроводе не может меняться в зависимости от времени. Массовый баланс между портами в этом простом случае:

${\dot{m}}_{A} + {\dot{m}}_{B} = 0,$

где $\dot{m}$ обозначает массовый расход жидкости в трубопровод, и индекс обозначает порт, в котором задано его значение. Если трубопроводу дают радиально совместимую стенку — то есть, если параметры блоков Pipe wall specification изменяются на Flexible— тепловая жидкая масса, содержавшая в ее границах, свободна варьироваться, в какой-то мере всегда прямо пропорциональная объему трубопровода:

${\dot{m}}_{A} + {\dot{m}}_{B} = ρ_{I} \dot{V},$

где ρ является тепловой плотностью в объеме трубопровода (индекс I), обозначил V. Если, кроме того, тепловая жидкость сделана сжимаемой — если параметры блоков Fluid dynamic compressibility изменяются на On— его масса в трубопроводе должна измениться с давлением и температурой также. Эта зависимость получена модулем объемной упругости и тепловым коэффициентом расширения тепловой жидкости:

${\dot{m}}_{A} + {\dot{m}}_{B} = ρ_{I} \dot{V} + ρ_{I} V (\frac{{\dot{p}}_{I}}{β_{I}} - α_{I} {\dot{T}}_{I}),$

где p и T обозначают давление и температуру в объеме трубопровода, и β и α обозначают модуль объемной упругости и тепловой коэффициент расширения (как предусмотрено к тепловой жидкой сети блоком Thermal Liquid Settings (TL) или Thermal Liquid Properties (TL)).

Баланс импульса

Тепловой жидкий поток подвергается различным силам, когда он пересекает трубопровод. Они возникают из-за статического давления в портах, вязкого трения вдоль стенки трубопровода и силы тяжести на объеме трубопровода. Инерционная сила на жидкости по умолчанию проигнорирована, подходящее приближение в больших масштабах времени, по которым обычно происходят изменения течь. Трубопровод затем обработан как квазиустойчивый компонент и его баланс импульса — выраженный, когда перепад давлений между его портами — становится:

$p_{A} - p_{B} = p_{F,A} - p_{F,B} + ρ_{I} g Δ z,$

где p является давлением в порте и p _F падение давления на трение в половине объема трубопровода; g является гравитационным ускорением и Δz повышение вертикального изменения от порта A до порта B. Индексы обозначают порт (A или B) или вычислительный узел, соответствующий внутреннему объему жидкости (I). Давление принято в этом простом случае, чтобы варьироваться линейно между портами. Его значение во внутреннем узле — используемом в поиске по таблице ρ _I — поэтому задано как среднее арифметическое давлений в портах:

$p_{I} = \frac{p_{A} + p_{B}}{2} .$

Если поток обработан как сжимаемый — если параметры блоков Fluid dynamic compressibility изменяются на On— давление в трубопроводе может варьироваться нелинейно между портами. Его значение больше не является простым средним арифметическим, и оно должно быть получено явным образом другим, означает. Чтобы выполнить это вычисление, баланс импульса разделен по двум объемам управления, один каждый для половины объема трубопровода. Между портом A и внутренним узлом:

$p_{A} - p_{I} = p_{F,A} + ρ_{I} g \frac{Δ z}{2} .$

Между портом B и внутренним узлом:

$p_{B} - p_{I} = p_{F,B} - ρ_{I} g \frac{Δ z}{2} .$

Если кроме того, инерция жидкости включена в вычисления — то есть, если параметры блоков Fluid inertia установлены в On— затем изменения в импульсе потока больше не принимаются, чтобы быть мгновенными. Переходная фаза между старыми и новыми устойчивыми состояниями становится постепенной с коротким, но ненулевым масштабом времени, который зависит частично от смоделированной системы. Баланс импульса становится в объеме управления, смежном с портом A:

$p_{A} - p_{I} = p_{F,A} + ρ_{I} g \frac{Δ z}{2} + \frac{{\ddot{m}}_{A}}{S} \frac{L}{2},$

где L является длиной трубопровода, и S является площадью поперечного сечения потока через то же самое. Инвертирование знака срока вертикального изменения дает для объема управления, смежного с портом B:

$p_{B} - p_{I} = p_{F,B} - ρ_{I} g \frac{Δ z}{2} + \frac{{\ddot{m}}_{B}}{S} \frac{L}{2},$

Падение давления трения в стенке трубопровода

Вычисление главного падения давления (из-за трения в трубопроводе) меняется в зависимости от вязкой параметризации трения. Для всей параметризации, но Nominal pressure drop vs. nominal mass flow rate, вычисление основано на уравнении Дарси-Weisbach:

$p_{F, j} = f_{D, j} \frac{1}{4} \frac{L_{E} {\dot{m}}_{j} | {\dot{m}}_{j} |}{ρ_{I} D S^{2}},$

где f _D является коэффициентом трения Дарси и индексом, j обозначает трубопровод половина — что смежный с портом A или с портом B. L _E является эффективной длиной трубопровода, и D является гидравлическим диаметром того же самого. Эффективная длина трубопровода как сумма истинной длины трубопровода и совокупная эквивалентная продолжительность всех локальных сопротивлений (те из-за колен, объединений, подборов кривой и других локальных источников трения).

Когда поток ламинарен, коэффициент трения (для данной геометрии трубопровода) является функцией одного только числа Рейнольдса:

$f_{D, j} = \frac{λ}{{Re}_{j}},$

где λ является масштабным фактором трубопровода, эмпирическая константа раньше кодировала эффект геометрии трубопровода на главном падении давления; его значением является 64 в круглых сечениях и 48–96 в некруговых единицах. Число Рейнольдса в порте k задано как:

${Re}_{j} = \frac{{\dot{m}}_{j} D}{μ_{I} S},$

где μ является динамической вязкостью, полученной из блока Thermal Liquid Settings (TL) или Thermal Liquid Properties (TL). Фактическое вычисление падения давления в ламинарном режиме течения жидкости выполняется как:

$p_{F, j} = \frac{1}{4} \frac{λ μ_{I} L_{E} {\dot{m}}_{j}}{ρ_{I} D^{2} S},$

Когда поток турбулентен, коэффициент трения является функцией также диаметра трубопровода и поверхностной шероховатости. Если вязкая параметризация трения установлена в Haaland correlation, коэффициент трения вычисляется от эмпирического выражения:

$\frac{1}{\sqrt{f_{D, j}}} = - 1.8 журнал [{(\frac{\frac{ϵ}{D}}{3.7})}^{1.11} + \frac{6.9}{{Re}_{j}}],$

где ε является абсолютной шероховатостью трубопровода, мерой высоты ударов в жидком трубопроводом интерфейсе; типичные значения шероховатости лежат в диапазоне от 0,0015 мм для определенных пластмассовых и стеклянных труб к 3 мм для больших конкретных трубопроводов. Если вязкая параметризация трения установлена в Tabulated data – Darcy friction factor vs. Reynolds number, коэффициент трения получен из табличных данных как функция числа Рейнольдса:

$f_{D} = f (Ре) .$

Если вязкая параметризация трения установлена в Nominal pressure drop vs. nominal mass flow rate, главное падение давления вычисляется для каждого трубопровода половина от выражения:

$p_{F, j} = \frac{1}{2} K_{p} {\dot{m}}_{j} \sqrt{{\dot{m}}_{j}^{2} + {\dot{m}}_{Th}^{2}}$

где ${\dot{m}}_{Th}$ пороговый массовый расход жидкости, маленькое значение, заданное в диалоговом окне блока, которое используется в числовых целях сглаживания; K _p является коэффициентом падения давления, вычисленным для твердых трубопроводов как:

$K_{p} = \frac{p_{F,N}}{{\dot{m}}_{N}^{2}},$

где индекс N обозначает значение, заданное в некоторых номинальных условиях работы. Если номинальное давление и массовый расход жидкости являются скалярными значениями, коэффициент падения давления определяется предыдущим уравнением. Если номинальное давление и массовый расход жидкости являются векторными количествами, коэффициент падения давления определяется припадком наименьших квадратов векторов, который устанавливает оптимальное значение K _p, чтобы применяться в изменяющихся условиях. K _p остается постоянным в течение симуляции.

Коэффициент падения давления переопределен для шлангов (с небольшим изменением в физических единицах измерения) как:

$K_{p} = \frac{p_{F,N}}{{\dot{m}}_{N}^{2}} D_{N} .$

Гидравлический диаметр стенки трубопровода

Гидравлический диаметр является мерой ширины для трубопроводов, сечения которых не могут быть круговыми. Обратите внимание на то, что только твердым трубопроводам позволяют быть некруговыми в сечении. Диаметр шланга может варьироваться в процессе моделирования как функция давления с такими изменениями, принятыми, чтобы быть универсальным в длине трубопровода. Деформация трубопровода продолжает на уровне, установленном частично вязкоупругой постоянной времени:

$\dot{D} = \frac{D_{S} - D_{N}}{τ},$

где τ является постоянной времени и индексами S и N обозначьте значения при установившихся и номинальных условиях, соответственно. Номинальная стоимость дает диаметр при нулевом абсолютном давлении (когда давление в компоненте равно атмосферному давлению). Установившееся значение дает диаметр при фактическом абсолютном давлении после того, как переходный процесс прекратился:

$D_{S} = K_{c} \frac{p - p_{0}}{τ},$

где K _c является эластичной податливостью стенки трубопровода, номер, указывающий на степень, до которой изменение в давлении влияет на диаметр трубопровода. Этот параметр может быть вычислен при необходимости от других свойств упругости стенки:

$K_{c} = \frac{D_{0,Int}}{E} (\frac{D_{0,Ext}^{2} + D_{0, Int}^{2}}{D_{0, Расширение}^{2} - D_{0, Int}^{2}} + ν),$

где E и ν являются модулем эластичности и отношением Пуассона стенного материала трубопровода. Индекс 0 обозначает начальное значение, соответствуя условиям в модели в начале симуляции (чтобы не быть перепутанным с номинальными условиями, при которых D _N задан). Индексы Int и Ext обратитесь к внутренним и внешним окружностям стенки трубопровода.

Номинальный диаметр трубопровода (используемый в вычислении уровня деформации трубопровода) вычисляется как:

$D_{N} = \sqrt{\frac{4 S}{π}},$

где S является заданной площадью поперечного сечения трубопровода (номинальная стоимость в трубопроводах, которые обработаны как гибкие).

Энергетический баланс

Энергия жидкости в трубопроводе может измениться множеством процессов. Они включают адвекцию и проводимость через концы трубопровода (тепловые гидравлические порты A и B), конвекция в жидком трубопроводом интерфейсе (тепловой порт H), и, в трубопроводах, которые установлены под углом, продольными разницами в вертикальном положении. Выражение энергетического баланса в терминах энергетической скорости накопления в трубопроводе дает:

$\dot{E_{I}} = ϕ_{A} + ϕ_{B} + ϕ_{H} - \dot{m_{I}} g Δ z,$

где $\dot{E}$ энергетическая скорость накопления, и ϕ является энергетической скоростью потока жидкости через порт — сглаживавший и против ветра в тепловых гидравлических портах, как описано в энергетических Потоках в Тепловых Жидких Сетях. Как в массе и вычислениях импульса, индекс I обозначает значение, заданное во внутреннем вычислительном узле. Массовый расход жидкости в термине потенциальной энергии является средним значением установленных в тепловых гидравлических портах:

${\dot{m}}_{I} = \frac{{\dot{m}}_{A} + {\dot{m}}_{B}}{2} .$

Полная энергия внутреннего объема жидкости задана в терминах определенной внутренней энергии как:

$E_{I} = ρ_{I} u_{I} V,$

где u является определенной внутренней энергией жидкости, полученной как функция температуры и давления блока Thermal Liquid Settings (TL) или Thermal Liquid Properties (TL), и V является внутренним объемом трубопровода. Если поток обработан как сжимаемый — если параметры блоков Flow dynamic compressibility установлены в On— затем энергетическая скорость накопления в трубопроводе вычисляется как:

${\dot{E}}_{I} = ρ_{I} V {(\frac{d u}{d p} \frac{d p}{d t} + \frac{d u}{d T} \frac{d T}{d t})}_{I},$

Если, кроме того, трубопроводу дают совместимую стенку — если параметры блоков Pipe wall specification установлены в Flexible— затем объем тепловой жидкости в ее границах свободен варьироваться. Энергетическая скорость накопления становится:

${\dot{E}}_{I} = ρ_{I} V {(\frac{d u}{d p} \frac{d p}{d t} + \frac{d u}{d T} \frac{d T}{d t})}_{I} + (ρ_{I} u_{I} + p_{I}) {(\frac{d V}{d t})}_{I},$

Конвективная теплопередача в стенке трубопровода

Уровень теплового потока между тепловой жидкостью и стенкой трубопровода принят, чтобы следовать из конвективного обмена и чисто проводящего обмена:

$ϕ_{H} = Q_{Conv} + Q_{Cond} .$

Уровень теплового потока из-за проводимости вычисляется как:

$Q_{Cond} = \frac{k_{I} S_{H}}{D} (T_{H} - T_{I}),$

где k является теплопроводностью тепловой жидкости, и S _H является площадью поверхности стенки трубопровода (продукт периметра и длина трубопровода, чтобы не быть перепутанным с площадью поперечного сечения того же самого). Индексы H и I обозначьте стенку трубопровода и внутренний объем жидкости, соответственно.

Уровень теплового потока из-за конвекции вычисляется как:

$Q_{Conv} = c_{p,Avg} | {\dot{m}}_{Avg} | (T_{H} - T_{In}) [1 - exp (- \frac{h S_{H}}{c_{p,Avg} | {\dot{m}}_{Avg} |})],$

где c _p является удельной теплоемкостью тепловой жидкости, _h является коэффициентом теплопередачи трубопровода. Индекс В обозначает вход трубопровода (порт A или B в зависимости от направления потока). Параметры с индексом В среднем оценены при средней температуре трубопровода. Это выражение основано на предположении, что температура варьируется экспоненциально между концами трубопровода.

Для всей параметризации теплопередачи, но Nominal temperature differential vs. nominal mass flow rate, коэффициент теплопередачи вычисляется из выражения:

$h = \frac{{Nu}_{Avg} k_{Avg}}{D},$

где Nu является номером Nusselt и k теплопроводность в трубопроводе, оба полученные при средней температуре в нем. Вычисление номера Nusselt меняется в зависимости от выбранной параметризации:

Gnielinski correlation:
В турбулентном режиме:

${Nu}_{Avg} = \frac{\frac{f_{Avg}}{8} ({Re}_{Avg} - 1000) {Pr}_{В среднем}}{1 + 12.7 {(\frac{f_{Avg}}{8})}^{1 / 2} ({Pr}_{В среднем}^{2 / 3} - 1)},$
где Pr является числом Прандтля. В ламинарном режиме течения жидкости, в котором не применяется корреляция, номер Nusselt получен как константа (обозначил Nu _L) от параметров блоков Nusselt number for laminar flow heat transfer:

${Nu}_{Avg} = {Nu}_{L},$
Dittus-Boelter correlation:
В турбулентном режиме:

${Nu}_{Avg} = a {Ре}_{В среднем}^{b} {PR}_{В среднем}^{c},$
где a, b и c являются эмпирическими константами, характерными для рассмотренной системы. Значения по умолчанию, заданные в блоке, являются используемыми в точной форме выражения Dittus-Boelter для жидкости, подогреваемой стенкой трубопровода:

${Nu}_{Avg} = 0.023 {Ре}_{В среднем}^{0.8} {PR}_{В среднем}^{0.4} .$
Как с корреляцией Гниелинского, в ламинарном режиме течения жидкости, в котором не применяется корреляция, номер Nusselt получен как константа (обозначил Nu _L) от параметров блоков Nusselt number for laminar flow heat transfer.
Tabulated data - Colburn factor vs. Reynolds number:
Во всех режимах течения:

${Nu}_{Avg} = J_{M, В среднем} ({Re}_{В среднем}) {Re}_{В среднем} {PR}_{В среднем}^{1 / 3} .$
где J _M является коэффициентом Колборна-Чилтона.
Tabulated data - Nusselt number vs. Reynolds number & Prandtl number:
Во всех режимах течения:

${Nu}_{Avg} = \nu ({Re}_{В среднем}, {Pr}_{В среднем}) .$

Вычисления отличаются немного в случае Nominal temperature difference vs. nominal mass flow rate параметризация. В ламинарном режиме течения жидкости коэффициент теплопередачи является той же константой, заданной в другой параметризации (параметры блоков Nusselt number for laminar flow heat transfer). В режиме турбулентного течения это вычисляется как функция массового расхода жидкости с пропорциональностью между этими двумя, зафиксированными формой корреляции Диттуса-Болтера:

$Nu \propto {Ре}^{0.8},$

или:

$\frac{h D}{k} \propto {(\frac{\dot{m} D}{S μ})}^{0.8}$

Реорганизация условий:

$h = K_{H,Avg} \frac{{\dot{m}}_{В среднем}^{0.8}}{D^{1.8}},$

где K _H является коэффициентом пропорциональности, созданным путем смешивания всех параметров, но сохраненных в итоговом выражении (со свойствами жидкости, заданными при средней температуре в трубопроводе). Константа вычисляется из номинальной стоимости, полученной для h, D, и $\dot{m}$ как:

$K_{H,Avg} = \frac{h_{N} D_{N}^{1.8}}{{\dot{m}}_{N}^{0.8}},$

Коэффициент теплопередачи для Nominal temperature difference vs. nominal mass flow rate параметризация поэтому:

$h = \frac{h_{N} D_{N}^{1.8}}{{\dot{m}}_{N}^{0.8}} \frac{{\dot{m}}_{I}^{0.8}}{D^{1.8}},$

или, в более простом случае трубопровода, обработанного как твердый (и поэтому принятый постоянным в диаметре):

$h_{I} = \frac{h_{N}}{{\dot{m}}_{N}^{0.8}} {\dot{m}}_{I}^{0.8} .$

Номинальный массовый расход жидкости получен из табличных данных, заданных через параметры блоков Nominal mass flow rate. Номинальный коэффициент теплопередачи вычисляется от различных номинальных параметров как:

$h_{N} = \frac{{\dot{m}}_{N} c_{p,N}}{S_{H,N}} ln (\frac{T_{H,N} - T_{In, N}}{T_{H,N} - T_{Out,N}}),$

где c _p является удельной теплоемкостью при постоянном давлении и индексах H\in, и Out обозначьте стенку, вход (какой бы ни из тепловых гидравлических портов, оказывается, он в данный момент), и выход. Номинальная площадь поверхности стенки трубопровода (S _{{H, N}}) вычисляется как продукт окружности трубопровода и длины трубопровода:

$S_{H,N} = \frac{4 S}{D} L,$

Гидравлический диаметр (D) является константой, если трубопровод тверд, но функция давления, если трубопровод гибок. Его значение получено из параметров блоков Hydraulic diameter, если параметр Pipe wall specification устанавливается на Rigid и вычисленный из параметра Nominal cross-sectional area в противном случае, предоставления, для шланга:

Порты

Входной параметр

развернуть все

`El` — Различие в вертикальном изменении порта
физический сигнал

Управляющий сигнал, для которого можно установить мгновенное различие в вертикальном изменении между тепловыми гидравлическими портами. В зависимости от блоков, используемых, чтобы сгенерировать сигнал, различие в вертикальном изменении может быть постоянным, или это может меняться в зависимости от времени. Если порт оставляют несвязанным, различие в вертикальном изменении фиксируется в нуле в процессе моделирования.

Сохранение

развернуть все

`A` — Открытие трубопровода
тепловая жидкость

Открытие, посредством которого тепловая жидкость течет в или из трубопровода. Порты A и B могут каждый функционировать или как вход или как выход. Тепловая проводимость позволена между тепловыми гидравлическими портами и жидкостью, внутренней к трубопроводу (хотя его удар обычно релевантен только в почти нулевых скоростях потока жидкости).

`B` — Открытие трубопровода
тепловая жидкость

`H` — Передайте стенку по каналу
тепловой

Тепловой контур между объемом жидкости и стенкой трубопровода. Используйте этот порт, чтобы получить теплообмены различных видов — например, проводящий, конвективный, или радиационный — между жидкостью и средой, внешней к трубопроводу (учитывающий тепловое сопротивление стенки, когда это будет значительно).

Параметры

развернуть все

Настройка

`Fluid dynamic compressibility` — Опция, чтобы получить изменения плотности из-за давления
`On` (значение по умолчанию) | `Off`

Опция, чтобы получить изменения плотности из-за тех в давлении. Динамическая сжимаемость предоставляет блок более реалистическому, хотя также более в вычислительном отношении требуя, симуляциям. Выберите Off если скорость симуляции вызывает беспокойство, когда это обычно - в режиме реального времени симуляция, и если динамическая сжимаемость не есть большого значения в результатах модели.

`Fluid inertia` — Опция, чтобы получить сопротивление жидкости к изменениям в ее движении
`On` (значение по умолчанию) | `Off`

Опция, чтобы получить сопротивление жидкости к изменениям в ее состоянии движения, например, в системах, подверженных гидравлическому удару. Инерция жидкости предоставляет блок более реалистическому, хотя также более в вычислительном отношении требуя, симуляциям. Выберите Off если скорость симуляции вызывает беспокойство, когда это обычно - в режиме реального времени симуляция, и если инерция жидкости не есть большого значения в результатах модели.

Зависимости

Этот параметр активен, когда параметры блоков Fluid dynamic compressibility установлены в On.

`Number of segments` — Количество длин, в которые можно дискретизировать трубопровод
1 (значение по умолчанию) | положительный безразмерный скаляр

Количество длин, в которые можно дискретизировать трубопровод. Каждая длина соответствует объему жидкости с вычислительным узлом — точка в компоненте, в котором давлении и температуре оценены в процессе моделирования. Увеличьте число сегментов трубопровода, чтобы более точно получить продольные распределения давления и температуры, например, в симуляции гидравлического удара, в котором имеют значение такие распределения.

Зависимости

Этот параметр активен, когда параметры блоков Fluid dynamic compressibility установлены в On.

`Pipe total length` — Расстояние между портами трубопровода
`5 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Сумма длин сегментов, включающих трубопровод.

`Nominal cross-sectional area` — Область внутренней окружности сечения трубопровода
0.01 м^2 (значение по умолчанию) | положительная скалярная величина в единицах площади

Область внутренней окружности сечения трубопровода (в недеформированном состоянии, если смоделировано с совместимой стенкой).

`Pipe wall specification` — Опция, чтобы получить радиальную податливость стенки трубопровода
`Rigid` (значение по умолчанию) | `Flexible`

Опция, чтобы получить радиальную податливость стенки трубопровода. Настройка по умолчанию On соответствует гибкой трубе, стенка которой расширяется и сокращается как функция давления. Выберите Off если скорость симуляции вызывает беспокойство, когда это обычно - в режиме реального времени симуляция, и если пограничное течение не есть большого значения в (или нетипичный из) модель.

Зависимости

Этот параметр активен, когда параметры блоков Fluid dynamic compressibility установлены в On.

`Hydraulic diameter` — Отношение площади открытия трубопровода к периметру того же самого
`0.1128 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Отношение площади открытия трубопровода к внутреннему периметру (поперечное сечение) то же самое. Этот параметр дает общую меру ширины для трубопроводов с некруглыми сечениями.

Зависимости

Этот параметр активен, когда параметры блоков Fluid dynamic compressibility установлены в Off или когда это установлено в On но параметры блоков Pipe wall specification установлены в Rigid.

`Elevation gain from port A to port B` — Изменитесь в вертикальном изменении трубопровода в направлении порта А к порту B
`0 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Изменитесь в вертикальном изменении трубопровода в направлении порта A к порту B. Этот параметр допускает вычисление скачка давления из-за вертикального изменения в трубопроводе. Значение по умолчанию 0 соответствует трубопроводу, положенному плоский.

Зависимости

Этот параметр отсоединен в диалоговом окне блока, когда вариант блока установлен в Constant elevation. Измените вариант блока в Variable elevation при необходимости, например, чтобы получить наклон трубопровода в в процессе моделирования.

`Gravitational acceleration` — Ускорение из-за силы тяжести при среднем вертикальном изменении трубопровода
`9.81 m/s^2` (значение по умолчанию) | положительная скалярная величина в модулях length/time^2

Значение ускорения свободного падения (g) при среднем вертикальном изменении трубопровода. Любые разницы в вертикальном положении приняты, чтобы достаточно быть малыми, что получение по запросу силы тяжести является приблизительно постоянным.

`Static pressure-diameter compliance` — Мера деформации, вызванной в трубопроводе модулем, изменяется в давлении
`1.2e-6 m/MPa` (значение по умолчанию) | положительная скалярная величина в единицах длины/давления

Мера радиальной деформации, вызванной в трубопроводе модулем, изменяется в давлении в нем относительно его среды. Этот параметр является свойством материала, из которого сделана стенка трубопровода.

Зависимости

Этот параметр активен, когда параметры блоков Pipe wall specification установлены в Flexible.

`Viscoelastic process time constant` — Мера времени, за которое трубопровод, как ожидают, будет деформироваться
`0.01 s` (значение по умолчанию) | положительная скалярная величина в модулях времени

Характеристический масштаб времени эластичных деформаций производится на стенке трубопровода. Этот параметр дает грубую меру времени, необходимого для трубопровода, нарушенного скачком давления, чтобы достигнуть нового установившегося диаметра.

Зависимости

Этот параметр активен, когда параметры блоков Pipe wall specification установлены в Flexible.

Вязкое трение

`Viscous friction parameterization` — Метод, которым можно получить падение давления на трение против стенки трубопровода
`Haaland correlation` (значение по умолчанию) | `Nominal pressure drop vs. nominal mass flow rate` | `Tabulated data - Darcy friction factor vs. Reynolds number`

Метод, которым можно получить падение давления в трубопроводе из-за трения против стенки. Вычисление может быть основано на эмпирической корреляции (тот из Haaland) или на сведенной в таблицу функции (обеспечение или перепад давления или коэффициент трения Дарси).

`Aggregate equivalent length of local resistances` — Незначительное падение давления в трубопроводе, выраженном как длина
`1 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Незначительное падение давления в трубопроводе, выраженном как длина. Этот параметр служит, чтобы настроить эффективную длину трубопровода и от него, чтобы вычислить общее падение давления между портами.

Зависимости

Этот параметр активен, когда параметры блоков Viscous friction parameterization установлены в Haaland correlation.

`Internal surface absolute roughness` — Характеристическая высота микроскопических выступов на внутренней поверхности трубопровода
`1.5e-5 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Характеристическая высота микроскопических выступов на внутренней поверхности трубопровода. Этот параметр служит, чтобы вычислить падение давления на трение против стенки трубопровода.

Зависимости

Этот параметр активен, когда параметры блоков Viscous friction parameterization установлены в Haaland correlation.

`Shape factor for laminar flow viscous friction` — Эмпирическая мера эффектов геометрии на падениях давления на трение
64 (значение по умолчанию) | положительный безразмерный скаляр

Эмпирическая мера эффектов геометрии на падениях давления на трение. Типичные значения лежат в диапазоне от 48 к 96. Значение по умолчанию, 64, соответствует трубопроводу круглого сечения.

`Laminar flow upper Reynolds number limit` — Число Рейнольдса, ниже которого поток ламинарен
`2e+3` (значение по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, ниже которого поток ламинарен. Выше этого порога, переходов потока к турбулентному, достигая истинного турбулентного режима при установке Turbulent flow lower Reynolds number limit.

`Turbulent flow lower Reynolds number limit` — Число Рейнольдса, выше которого поток турбулентен
`4e+3` (значение по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, выше которого поток турбулентен. Ниже этого порога, поток постепенно переходы к ламинарному, достигая истинного ламинарного режима при установке Laminar flow upper Reynolds number limit.

`Nominal mass flow rate` — Массовый расход (расходы) жидкости, от которого можно вычислить коэффициент падения давления трубопровода
`[0.1 1] kg/s` (значение по умолчанию) | скаляр или вектор чисел в единицах массы/времени

Массовый расход жидкости, в некоторых выбранных рабочих точках, от которых можно вычислить коэффициент падения давления трубопровода. Этот параметр может быть скаляром или вектором со скаляром, соответствующим одной рабочей точке и вектору ко множеству рабочих точек. mldivide MATLAB функция используется, чтобы решить для коэффициента падения давления, если вектор задан. Все номинальные параметры во вкладке Viscous Friction должны иметь тот же размер.

Зависимости

Этот параметр активен, когда параметры блоков Viscous friction parameterization установлены в Nominal pressure drop vs. nominal mass flow rate.

`Nominal pressure drop` — Перепад (перепады) давления, от которого можно вычислить коэффициент падения давления трубопровода
`[0.001 0.01] MPa` (значение по умолчанию) | скаляр или вектор чисел в единицах давления

Перепад давления, в некоторых выбранных рабочих точках, от которых можно вычислить коэффициент падения давления трубопровода. Этот параметр может быть скаляром или вектором со скаляром, соответствующим одной рабочей точке и вектору ко множеству рабочих точек. mldivide MATLAB функция используется, чтобы решить для коэффициента падения давления, если вектор задан. Все номинальные параметры во вкладке Viscous Friction должны иметь тот же размер.

Зависимости

`Mass flow rate threshold for flow reversal` — Массовый расход жидкости, ниже которого можно применить числовое сглаживание к вычислениям блока
`1e-6 kg/s` (значение по умолчанию) | положительная скалярная величина в единицах массы/времени

Массовый расход жидкости, ниже которого можно применить числовое сглаживание к вычислениям блока, мера, принятая, чтобы предотвратить ошибки симуляции из-за разрывов в нулевом потоке.

Зависимости

`Reynolds number vector for turbulent Darcy friction factor` — Числа Рейнольдса, в которых можно свести в таблицу коэффициент трения Дарси
`[ 400 1000 1.5e+3 3e+3 4e+3 6e+3 1e+4 2e+4 4e+4 6e+4 1e+5 1e+8 ]` (значение по умолчанию) | вектор положительных безразмерных чисел

Число Рейнольдса, в котором можно свести в таблицу коэффициент трения Дарси. Эти данные служат, чтобы создать одностороннюю интерполяционную таблицу, от которой можно вычислить коэффициент трения Дарси и в конечном счете падение давления через трубопровод. Вектор должен увеличиться монотонно слева направо. Это и вектор коэффициента трения Дарси должны иметь тот же размер.

Зависимости

Этот параметр активен, когда параметры блоков Viscous friction parameterization установлены в Tabulated data - Darcy friction factor vs. Reynolds number.

`Darcy friction factor vector` — Коэффициенты трения дарси в сведенных в таблицу числах Рейнольдса
[ 0.264 0.112 0.07099999999999999 0.0417 0.0387 0.0268 0.025 0.0232 0.0226 0.022 0.0214 0.0214 ] (значение по умолчанию) | вектор положительных безразмерных чисел

Коэффициенты трения Дарси в сведенных в таблицу значениях числа Рейнольдса. Эти данные служат, чтобы создать одностороннюю интерполяционную таблицу, от которой можно вычислить коэффициент трения Дарси и в конечном счете падение давления через трубопровод. Это и число Рейнольдса должны иметь тот же размер.

Зависимости

Теплопередача

`Heat transfer parameterization` — Метод, которым можно получить конвективную теплопередачу со стенкой трубопровода
`Gnielinski correlationNominal temperature differential vs. nominal mass flow rate` (значение по умолчанию) | `Dittus-Boelter correlation` | `Tabulated data - Colburn factor vs. Reynolds number` | `Tabulated data - Nusselt number vs. Reynolds number & Prandtl number`

Метод, которым можно вычислить конвективный коэффициент теплопередачи трубопровода. Вычисление может быть основано на эмпирической корреляции (которых те из Гниелинского и Диттус-Боелтера являются опциями), или на сведенной в таблицу функции (обеспечение температурного дифференциала, коэффициента Колборна или номера Nusselt).

`Nusselt number for laminar flow heat transfer` — Номер Nusselt, чтобы использовать в вычислениях теплопередачи в ламинарных течениях
3.66 (значение по умолчанию)

Номер Nusselt для ламинарных течений в трубе. Этот номер служит, чтобы вычислить коэффициент теплопередачи между стенкой трубопровода и жидкостью в ней. Значение по умолчанию 3.66 соответствует потоку через трубу круглого сечения.

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Gnielinski correlation, Nominal temperature differential vs. nominal mass flow rate, или Dittus-Boelter correlation.

`Nominal mass flow rate` — Массовый расход (расходы) жидкости, от которого можно вычислить коэффициент теплопередачи
`[0.1 1] kg/s` (значение по умолчанию) | скаляр или вектор чисел в единицах массы/времени

Массовые расходы жидкости, в некоторой выбранной рабочей точке, от которой можно вычислить коэффициент теплопередачи трубопровода. Этот параметр может быть скаляром или вектором со скаляром, соответствующим одной рабочей точке и вектору ко множеству рабочих точек. mldivide MATLAB функция используется, чтобы решить для коэффициента теплопередачи, если вектор вектор задан. Все номинальные параметры во вкладке Heat Transfer должны иметь тот же размер.

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Nominal temperature differential vs. nominal mass flow rate.

`Nominal inflow temperature` — Передайте по каналу температуру (температуры) входа, от которой можно вычислить коэффициент теплопередачи
`[293.15 293.15] K` (значение по умолчанию) | скаляр или вектор чисел в единицах температуры

Передайте температуры входа по каналу в некоторых выбранных рабочих точках, от которых можно вычислить коэффициент теплопередачи трубопровода. Этот параметр может быть скаляром или вектором со скаляром, соответствующим одной рабочей точке и вектору ко множеству рабочих точек. mldivide MATLAB функция используется, чтобы решить для коэффициента теплопередачи, если вектор задан. Все номинальные параметры во вкладке Heat Transfer должны иметь тот же размер.

Зависимости

`Nominal outflow temperature` — Передайте по каналу выходную температуру (температуры), от которой можно вычислить коэффициент теплопередачи
`[300 300] K`'(значение по умолчанию) | скаляр или вектор чисел в единицах температуры

Передайте выходные температуры по каналу в некоторых выбранных рабочих точках, от которых можно вычислить коэффициент теплопередачи трубопровода. Этот параметр может быть скаляром или вектором со скаляром, соответствующим одной рабочей точке и вектору ко множеству рабочих точек. mldivide MATLAB функция используется, чтобы решить для коэффициента теплопередачи, если вектор задан. Все номинальные параметры во вкладке Heat Transfer должны иметь тот же размер.

Зависимости

`Nominal inflow pressure` — Передайте по каналу давление (давления) входа, от которого можно вычислить коэффициент теплопередачи
`[0.101325 0.101325] MPa` (значение по умолчанию) | скаляр или вектор чисел в единицах давления

Передайте давления входа по каналу в некоторых выбранных рабочих точках, от которых можно вычислить коэффициент теплопередачи трубопровода. Этот параметр может быть скаляром или вектором со скаляром, соответствующим одной рабочей точке и вектору ко множеству рабочих точек. mldivide MATLAB функция используется, чтобы решить для коэффициента теплопередачи, если вектор задан. Все номинальные параметры во вкладке Heat Transfer должны иметь тот же размер.

Зависимости

`Nominal wall temperature` — Передайте по каналу температуру (температуры) стенки, от которой можно вычислить коэффициент теплопередачи
`[303.15 303.15] K` (значение по умолчанию) | скаляр или вектор чисел в единицах температуры

Передайте температуры стенки по каналу в некоторых выбранных рабочих точках, от которых можно вычислить коэффициент теплопередачи трубопровода. Этот параметр может быть скаляром или вектором со скаляром, соответствующим одной рабочей точке и вектору ко множеству рабочих точек. mldivide MATLAB функция используется, чтобы решить для коэффициента теплопередачи, если вектор задан. Все номинальные параметры во вкладке Heat Transfer должны иметь тот же размер.

Зависимости

`Coefficient a` — Эмпирический постоянный a корреляции Диттуса-Болтера
0.023 (значение по умолчанию) | положительный безразмерный скаляр

Эмпирический постоянный a, чтобы использовать в корреляции Диттуса-Болтера. Корреляция дает значение номера Nusselt, от которого можно вычислить коэффициент теплопередачи в турбулентных потоках трубопровода. Значение по умолчанию - то, который чаще всего сопоставлял с этой корреляцией.

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Dittus-Boelter correlation.

`Exponent b` — Эмпирический постоянный b корреляции Диттуса-Болтера
0.8 (значение по умолчанию) | положительный безразмерный скаляр

Эмпирический постоянный c, чтобы использовать в корреляции Диттуса-Болтера. Корреляция дает значение номера Nusselt, от которого можно вычислить коэффициент теплопередачи в турбулентных потоках трубопровода. Значение по умолчанию - то, который чаще всего сопоставлял с этой корреляцией.

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Dittus-Boelter correlation.

`Exponent c` — Эмпирический постоянный c корреляции Диттуса-Болтера
0.4 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Dittus-Boelter correlation.

`Reynolds number vector for Colburn factor` — Числа Рейнольдса, в которых можно свести в таблицу коэффициент Колборна
[100 150 1000] (значение по умолчанию) | вектор положительных безразмерных чисел

Числа Рейнольдса, в которых можно свести в таблицу коэффициент Колборна. Эти данные служат, чтобы создать одностороннюю интерполяционную таблицу, от которой можно вычислить коэффициент Колборна и в конечном счете коэффициент теплопередачи. Вектор должен увеличиться монотонно слева направо. Это и вектор номера Colburn должны иметь тот же размер.

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Tabulated data - Colburn factor vs. Reynolds number.

`Colburn factor vector` — Коэффициенты Колборна, в который сведенные в таблицу числа Рейнольдса
[0.019 0.013 0.002] (значение по умолчанию) | вектор положительных безразмерных чисел

Коэффициенты Колборна в сведенных в таблицу значениях числа Рейнольдса. Эти данные служат, чтобы создать одностороннюю интерполяционную таблицу, от которой можно вычислить коэффициент Колборна и в конечном счете коэффициент теплопередачи. Это и вектор числа Рейнольдса должны иметь тот же размер.

Зависимости

`Reynolds number vector for Nusselt number` — Число Рейнольдса, в котором можно свести в таблицу номер Nusselt
[100 150 100] (значение по умолчанию) | вектор положительных безразмерных чисел

Числа Рейнольдса, при которых можно свести в таблицу число Нуссельта. Эти данные служат, чтобы создать двухстороннюю интерполяционную таблицу, из которой можно вычислить число Нуссельта и в конечном счете коэффициент теплопередачи. Вектор должен увеличиться монотонно слева направо. Этот вектор должен быть равен в размере количеству строк в таблице числа Нуссельта.

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

`Prandtl number vector for Nusselt number` — Числа Прандтля, в которых можно свести в таблицу номер Nusselt
[1 10] (значение по умолчанию) | вектор положительных безразмерных чисел

Числа Прандтля, в которых можно свести в таблицу номер Nusselt. Эти данные служат, чтобы создать двухстороннюю интерполяционную таблицу, из которой можно вычислить число Нуссельта и в конечном счете коэффициент теплопередачи. Вектор должен увеличиться монотонно слева направо. Этот вектор должен быть равен в размере количеству столбцов в таблице номера Nusselt.

Зависимости

`Nusselt number table` — Цифры Nusselt в сведенном в таблицу Рейнольдсе и числах Прандтля
[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (значение по умолчанию) | матрица положительных безразмерных чисел

Цифры Nusselt в сведенных в таблицу значениях Рейнольдса и чисел Прандтля. Эти данные служат, чтобы создать двухстороннюю интерполяционную таблицу, из которой можно вычислить число Нуссельта и в конечном счете коэффициент теплопередачи.

Число Рейнольдса изменяется от строки до строки сверху донизу. Номер Prandlt изменяется от столбца до столбца слева направо. Количество строк должно быть равно длине вектора числа Рейнольдса и количеству столбцов к длине вектора числа Прандтля.

Зависимости

Начальные условия

`Initial liquid temperature` — Абсолютная температура в трубопроводе в начале симуляции
`293.15 K` (значение по умолчанию) | положительная скалярная величина или вектор в единицах температуры

Абсолютная температура в трубопроводе в начале симуляции. Этот параметр может быть скаляром, вектором двух элементов или вектором, равным в размере к количеству сегментов в трубопроводе. Скаляр предписывает постоянную температуру от вплотную, двухэлементный вектор линейный градиент температуры, и вектор N оценивает отдельные температуры различных сегментов трубопровода.

`Initial liquid pressure` — Абсолютное давление в трубопроводе в начале симуляции
`0.101325 MPa` (значение по умолчанию) | положительная скалярная величина или вектор в единицах давления

Давление в трубопроводе в начале симуляции. Этот параметр может быть скаляром, вектором двух элементов или вектором, равным в размере к количеству сегментов в трубопроводе. Скаляр предписывает постоянное давление от вплотную, двухэлементный вектор линейный градиент давления, и вектор N оценивает отдельные давления различных сегментов трубопровода.

Документация

Pipe (TL)

Описание

Блокируйте варианты

Параметризация

Дискретизация трубопровода

Баланс массы

Баланс импульса

Падение давления трения в стенке трубопровода

Гидравлический диаметр стенки трубопровода

Энергетический баланс

Конвективная теплопередача в стенке трубопровода

Порты

Входной параметр

El — Различие в вертикальном изменении порта физический сигнал

Сохранение

A — Открытие трубопровода тепловая жидкость

B — Открытие трубопровода тепловая жидкость

H — Передайте стенку по каналу тепловой

Параметры

Настройка

Fluid dynamic compressibility — Опция, чтобы получить изменения плотности из-за давления On (значение по умолчанию) | Off

Fluid inertia — Опция, чтобы получить сопротивление жидкости к изменениям в ее движении On (значение по умолчанию) | Off

Зависимости

Number of segments — Количество длин, в которые можно дискретизировать трубопровод1 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Pipe total length — Расстояние между портами трубопровода 5 m (значение по умолчанию) | положительная скалярная величина в единицах длины

Nominal cross-sectional area — Область внутренней окружности сечения трубопровода0.01 м^2 (значение по умолчанию) | положительная скалярная величина в единицах площади

Pipe wall specification — Опция, чтобы получить радиальную податливость стенки трубопровода Rigid (значение по умолчанию) | Flexible

Зависимости

Hydraulic diameter — Отношение площади открытия трубопровода к периметру того же самого 0.1128 m (значение по умолчанию) | положительная скалярная величина в единицах длины

Зависимости

Зависимости

Зависимости

Зависимости

Вязкое трение

Зависимости

Зависимости

Shape factor for laminar flow viscous friction — Эмпирическая мера эффектов геометрии на падениях давления на трение64 (значение по умолчанию) | положительный безразмерный скаляр

Laminar flow upper Reynolds number limit — Число Рейнольдса, ниже которого поток ламинарен 2e+3 (значение по умолчанию) | положительный безразмерный скаляр

Turbulent flow lower Reynolds number limit — Число Рейнольдса, выше которого поток турбулентен 4e+3 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Зависимости

Зависимости

Зависимости

Зависимости

Теплопередача

Nusselt number for laminar flow heat transfer — Номер Nusselt, чтобы использовать в вычислениях теплопередачи в ламинарных течениях3.66 (значение по умолчанию)

Зависимости

Зависимости

Зависимости

Зависимости

Зависимости

Зависимости

Coefficient a — Эмпирический постоянный a корреляции Диттуса-Болтера0.023 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Exponent b — Эмпирический постоянный b корреляции Диттуса-Болтера0.8 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Exponent c — Эмпирический постоянный c корреляции Диттуса-Болтера0.4 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Зависимости

Colburn factor vector — Коэффициенты Колборна, в который сведенные в таблицу числа Рейнольдса[0.019 0.013 0.002] (значение по умолчанию) | вектор положительных безразмерных чисел

Зависимости

Reynolds number vector for Nusselt number — Число Рейнольдса, в котором можно свести в таблицу номер Nusselt[100 150 100] (значение по умолчанию) | вектор положительных безразмерных чисел

Зависимости

Prandtl number vector for Nusselt number — Числа Прандтля, в которых можно свести в таблицу номер Nusselt[1 10] (значение по умолчанию) | вектор положительных безразмерных чисел

Зависимости

Nusselt number table — Цифры Nusselt в сведенном в таблицу Рейнольдсе и числах Прандтля[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (значение по умолчанию) | матрица положительных безразмерных чисел

Зависимости

Начальные условия

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Введенный в R2016a

Документация Simscape Fluids

Поддержка

`El` — Различие в вертикальном изменении порта
физический сигнал

`A` — Открытие трубопровода
тепловая жидкость

`B` — Открытие трубопровода
тепловая жидкость

`H` — Передайте стенку по каналу
тепловой

`Fluid dynamic compressibility` — Опция, чтобы получить изменения плотности из-за давления
`On` (значение по умолчанию) | `Off`

`Fluid inertia` — Опция, чтобы получить сопротивление жидкости к изменениям в ее движении
`On` (значение по умолчанию) | `Off`

`Number of segments` — Количество длин, в которые можно дискретизировать трубопровод
1 (значение по умолчанию) | положительный безразмерный скаляр

`Pipe total length` — Расстояние между портами трубопровода
`5 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

`Nominal cross-sectional area` — Область внутренней окружности сечения трубопровода
0.01 м^2 (значение по умолчанию) | положительная скалярная величина в единицах площади

`Pipe wall specification` — Опция, чтобы получить радиальную податливость стенки трубопровода
`Rigid` (значение по умолчанию) | `Flexible`

`Hydraulic diameter` — Отношение площади открытия трубопровода к периметру того же самого
`0.1128 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

`Shape factor for laminar flow viscous friction` — Эмпирическая мера эффектов геометрии на падениях давления на трение
64 (значение по умолчанию) | положительный безразмерный скаляр

`Laminar flow upper Reynolds number limit` — Число Рейнольдса, ниже которого поток ламинарен
`2e+3` (значение по умолчанию) | положительный безразмерный скаляр

`Turbulent flow lower Reynolds number limit` — Число Рейнольдса, выше которого поток турбулентен
`4e+3` (значение по умолчанию) | положительный безразмерный скаляр

`Nusselt number for laminar flow heat transfer` — Номер Nusselt, чтобы использовать в вычислениях теплопередачи в ламинарных течениях
3.66 (значение по умолчанию)

`Coefficient a` — Эмпирический постоянный a корреляции Диттуса-Болтера
0.023 (значение по умолчанию) | положительный безразмерный скаляр

`Exponent b` — Эмпирический постоянный b корреляции Диттуса-Болтера
0.8 (значение по умолчанию) | положительный безразмерный скаляр

`Exponent c` — Эмпирический постоянный c корреляции Диттуса-Болтера
0.4 (значение по умолчанию) | положительный безразмерный скаляр

`Colburn factor vector` — Коэффициенты Колборна, в который сведенные в таблицу числа Рейнольдса
[0.019 0.013 0.002] (значение по умолчанию) | вектор положительных безразмерных чисел

`Reynolds number vector for Nusselt number` — Число Рейнольдса, в котором можно свести в таблицу номер Nusselt
[100 150 100] (значение по умолчанию) | вектор положительных безразмерных чисел

`Prandtl number vector for Nusselt number` — Числа Прандтля, в которых можно свести в таблицу номер Nusselt
[1 10] (значение по умолчанию) | вектор положительных безразмерных чисел

`Nusselt number table` — Цифры Nusselt в сведенном в таблицу Рейнольдсе и числах Прандтля
[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (значение по умолчанию) | матрица положительных безразмерных чисел

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.