Этот пример показывает, как симулировать управляемые силой тяжести орбиты главных тел солнечной системы. Модель обрабатывает солнце и планеты как совершенные сферы каждый с тремя поступательными степенями свободы. Вращение планеты проигнорировано. Поля тяготения генерируют силы, которые сохраняют планеты в орбите.

Блоки Spherical Solid представляют тела солнечной системы и обеспечивают их конфигурации, инерцию и цвета. блоки Cartesian Joint задают степени свободы тел относительно мировой системы координат, расположенной в барицентре солнечной системы. блоки Gravitational Field добавляют силы дальние, ответственные за изгиб начальных траекторий планеты на закрытые эллиптические орбиты.
Декартовы Блоки соединений обеспечивают начальные состояния — положения и скорости — солнца и планет относительно мировой системы координат. Начальные состояния соответствуют настройке солнечной системы 20-го июня 2016. Они получены от эфемеридных баз данных, обеспеченных Лабораторией реактивного движения (JPL).
Можно запросить базы данных через систему Горизонтов JPL с помощью интерфейса telnet или сети. Пользователи Aerospace Toolbox могут альтернативно получить эфемеридные данные в командной строке MATLAB® с помощью planetEphemeris функция после установки Космического Эфемеридного пакета Информационной поддержки.
Откройте шаблон модели Simscape™ Multibody™ и удалите все ненужные блоки. Измените настройки силы тяжести так, чтобы можно было добавить поля тяготения в модель. Результат обеспечивает начальную точку для модели солнечной системы.
В командной строке MATLAB введите smnew. MATLAB открывает шаблон модели с обычно используемыми блоками и подходящими настройками решателя для моделей Simscape Multibody.
Сократите все кроме Mechanism Configuration, Solver Configuration и блоков World Frame. Эти три блока предоставляют модели настройки силы тяжести, настройки решателя и глобальную систему координат инерции.
В диалоговом окне блока Mechanism Configuration, набор Uniform Gravity к None. Эта установка позволяет силе тяжести модели как сила закона обратных квадратов с помощью блоков Gravitational Field вместо этого.
Представляйте тела солнечной системы с помощью блоков Spherical Solid. Задайте геометрию и параметры инерции в терминах переменных MATLAB и инициализируйте эти переменные в рабочем пространстве модели с помощью Model Explorer. Переменные являются структурами данных, названными в честь тел солнечной системы с помощью капитализации имени собственного.
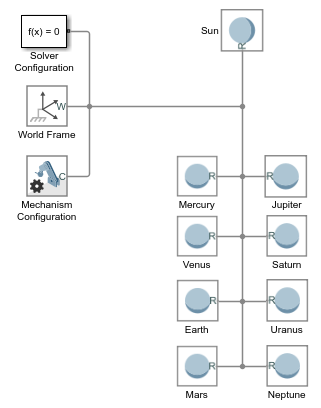
Добавьте в модель девять блоков Spherical Solid из библиотеки Body Elements. Блоки представляют солнце и восемь известных планет.
Соедините и назовите блоки как показано в фигуре. Разветвленная линия связи между мировой системой координат и планетами делает их жестко соединенными и совпадающими в пространстве. Вы позже изменяете это условие с помощью блоков Cartesian Joint.
В диалоговых окнах блока Spherical Solid, набор Inertia> параметр Based on к Mass. Установка параметра инерции позволяет вам задать твердую массу непосредственно так, чтобы можно было масштабировать формы планеты, не влияя на динамику модели.
Задайте следующие параметры блоков Spherical Solid в терминах полей структуры данных MATLAB. Введите имена полей в формат Structure.Field, где Structure является именем случая заголовка тела солнечной системы, и Field является строкой, показанной в таблице — например, Sun.R или Earth.RGB.
| Параметры блоков | Полевая строка |
|---|---|
| Geometry> Radius | R |
| Inertia> Mass | M |
| Graphic> Visual Properties> Color | RGB |
Вы позже задаете новые поля структуры в рабочем пространстве модели с помощью Model Explorer.
Во вкладке Modeling нажмите Model Explorer.
В панели Иерархии модели Model Explorer расширьте узел для своей модели и выберите Model Workspace. Панель Иерархии модели находится на левой стороне.
В панели Рабочего пространства модели Model Explorer, набор Data Source к MATLAB Code. Панель Рабочего пространства модели находится на правой стороне.
В поле MATLAB Code добавьте код инициализации для свойств тела солнца и планеты. Код организован в разделы, названные в честь тел солнечной системы. Вы позже добавляете данные об исходном положении и скорости в эти разделы.
% All values are in SI units. % RGB color vectors are on a normalized 0-1 scale. % Body dimensions are scaled for visualization purposes. % Scaling has no impact on model dynamics. % Scaling SunScaling = 0.5e2; TerrestrialPlanetScaling = 1.2e3; GasGiantScaling = 2.5e2; % Sun Sun.M = 1.99e30; Sun.R = 6.96e8*SunScaling; Sun.RGB = [1 0.5 0]; % Mercury Mercury.M =3.30e23; Mercury.R = 2.44e6*TerrestrialPlanetScaling; Mercury.RGB = [0.5 0.5 0.5]; % Venus Venus.M = 4.87e24; Venus.R = 6.05e6*TerrestrialPlanetScaling; Venus.RGB = [1 0.9 0]; % Earth Earth.M = 5.97e24; Earth.R = 6.05e6*TerrestrialPlanetScaling; Earth.RGB = [0.3 0.6 0.8]; % Mars Mars.M = 6.42e23; Mars.R = 3.39e6*TerrestrialPlanetScaling; Mars.RGB = [0.6 0.2 0.4]; % Jupiter Jupiter.M = 1.90e27; Jupiter.R = 6.99e7*GasGiantScaling; Jupiter.RGB = [0.6 0 0.3]; % Saturn Saturn.M = 5.68e26; Saturn.R = 5.82e7*GasGiantScaling; Saturn.RGB = [1 1 0]; % Uranus Uranus.M = 8.68e25; Uranus.R = 2.54e7*GasGiantScaling; Uranus.RGB = [0.3 0.8 0.8]; % Neptune Neptune.M = 1.02e26; Neptune.R = 2.46e7*GasGiantScaling; Neptune.RGB = [0.1 0.7 0.8];
Нажмите Reinitialize from Source.
Блоки Spherical Solid теперь имеют все числовые данные, они должны представить формы планеты и цвета. Попытайтесь открыть диалоговое окно блока Spherical Solid и проверьте, что сфера теперь появляется в твердой панели визуализации.
Заземлите серьезную визуализацию

Добавьте три поступательных степени свободы между барицентром солнечной системы и каждым телом солнечной системы с помощью блоков Cartesian Joint. Вы дальнейшее использование эти блоки, чтобы задать исходные положения и скорости тел солнечной системы.
Добавьте в модель девять блоков Cartesian Joint из библиотеки Joints. Блоки обеспечивают поступательные степени свободы солнца и восьми известных планет.
Соедините и назовите блоки как показано в фигуре. Если вы помещаете блок в существующую линию связи, программное обеспечение Simscape Multibody автоматически соединяет блок с той линией. Инвертируйте и вращайте блоки соединений, чтобы гарантировать, что блоки Spherical Solid соединяют только с последователем (F) порты системы координат.
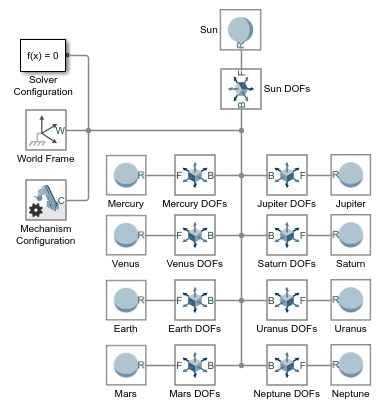
Солнце и планеты более не жестко соединены. Они могут теперь перевести друг относительно друга. Они являются, однако, все еще совпадающими в пространстве. Чтобы разместить их в различных исходных положениях и дать им начальные скорости, необходимо задать положения шарниров.
Задайте начальные состояния солнца и планеты в терминах переменных MATLAB с помощью Декартовых Блоков соединений в модели. Затем инициализируйте новые переменные MATLAB в рабочем пространстве модели с помощью Model Explorer. Вы задаете переменные MATLAB как новые поля в существующих структурах данных.
В диалоговых окнах блока Cartesian Joint проверяйте флажки State Targets> Specify Position Target и State Targets> Specify Velocity Target на эти X, Y, и призматические объединенные примитивы Z. Эти настройки позволяют вам задать желаемые начальные состояния солнца и планет.
Задайте целевые значения состояния Cartesian Joint для этих X, Y, и призматические объединенные примитивы Z в терминах полей структуры MATLAB. Введите имена полей в формат Structure.Field, где Structure является именем случая заголовка тела солнечной системы, и Field является строкой, показанной в таблице — например, Sun.Px или Earth.Vz.
| Соедините примитивную ось | Цель состояния | Полевая строка |
|---|---|---|
| X | Положение | Px |
| Скорость | Vx | |
| Y | Положение | Py |
| Скорость | Vy | |
| Z | Положение | Pz |
| Скорость | Vz |
Вы позже задаете новые поля структуры в рабочем пространстве модели с помощью Model Explorer.
Во вкладке Modeling нажмите Model Explorer.
В панели Иерархии модели Mechanics Explorer расширьте узел для своей модели и выберите Model Workspace. Панель Иерархии модели находится на левой стороне.
В панели Рабочего пространства модели Model Explorer, набор Data Source к MATLAB Code. Панель Рабочего пространства модели находится на правой стороне.
В поле MATLAB Code добавьте код инициализации для положений шарниров. Новый код, отображенный синим, состоит из компонентов положения и скорости, полученных из эфемеридных баз данных JPL. Можно скопировать только новый код или заменить целый код рабочего пространства модели на показанный.
% All values are in SI units. % RGB color vectors are on a normalized 0-1 scale. % Body dimensions are scaled for visualization purposes. % Scaling has no impact on model dynamics. % Scaling SunScaling = 0.5e2; TerrestrialPlanetScaling = 1.2e3; GasGiantScaling = 2.5e2; % Sun Sun.M = 1.99e30; Sun.R = 6.96e8*SunScaling; Sun.RGB = [1 0.5 0]; Sun.Px = 5.5850e+08; Sun.Py = 5.5850e+08; Sun.Pz = 5.5850e+08; Sun.Vx = -1.4663; Sun.Vy = 11.1238; Sun.Vz = 4.8370; % Mercury Mercury.M =3.30e23; Mercury.R = 2.44e6*TerrestrialPlanetScaling; Mercury.RGB = [0.5 0.5 0.5]; Mercury.Px = 5.1979e+10; Mercury.Py = 7.6928e+09; Mercury.Pz = -1.2845e+09; Mercury.Vx = -1.5205e+04; Mercury.Vy = 4.4189e+04; Mercury.Vz = 2.5180e+04; % Venus Venus.M = 4.87e24; Venus.R = 6.05e6*TerrestrialPlanetScaling; Venus.RGB = [1 0.9 0]; Venus.Px = -1.5041e+10; Venus.Py = 9.7080e+10; Venus.Pz = 4.4635e+10; Venus.Vx = -3.4770e+04; Venus.Vy = -5.5933e+03; Venus.Vz = -316.8994; % Earth Earth.M = 5.97e24; Earth.R = 6.05e6*TerrestrialPlanetScaling; Earth.RGB = [0.3 0.6 0.8]; Earth.Px = -1.1506e+09; Earth.Py = -1.3910e+11; Earth.Pz = -6.0330e+10; Earth.Vx = 2.9288e+04; Earth.Vy = -398.5759; Earth.Vz = -172.5873; % Mars Mars.M = 6.42e23; Mars.R = 3.39e6*TerrestrialPlanetScaling; Mars.RGB = [0.6 0.2 0.4]; Mars.Px = -4.8883e+10; Mars.Py = -1.9686e+11; Mars.Pz = -8.8994e+10; Mars.Vx = 2.4533e+04; Mars.Vy = -2.7622e+03; Mars.Vz = -1.9295e+03; % Jupiter Jupiter.M = 1.90e27; Jupiter.R = 6.99e7*GasGiantScaling; Jupiter.RGB = [0.6 0 0.3]; Jupiter.Px = -8.1142e+11; Jupiter.Py = 4.5462e+10; Jupiter.Pz = 3.9229e+10; Jupiter.Vx = -1.0724e+03; Jupiter.Vy = -1.1422e+04; Jupiter.Vz = -4.8696e+03; % Saturn Saturn.M = 5.68e26; Saturn.R = 5.82e7*GasGiantScaling; Saturn.RGB = [1 1 0]; Saturn.Px = -4.2780e+11; Saturn.Py = -1.3353e+12; Saturn.Pz = -5.3311e+11; Saturn.Vx = 8.7288e+03; Saturn.Vy = -2.4369e+03; Saturn.Vz = -1.3824e+03; % Uranus Uranus.M = 8.68e25; Uranus.R = 2.54e7*GasGiantScaling; Uranus.RGB = [0.3 0.8 0.8]; Uranus.Px = 2.7878e+12; Uranus.Py = 9.9509e+11; Uranus.Pz = 3.9639e+08; Uranus.Vx = -2.4913e+03; Uranus.Vy = 5.5197e+03; Uranus.Vz = 2.4527e+03; % Neptune Neptune.M = 1.02e26; Neptune.R = 2.46e7*GasGiantScaling; Neptune.RGB = [0.1 0.7 0.8]; Neptune.Px = 4.2097e+12; Neptune.Py = -1.3834e+12; Neptune.Pz = -6.7105e+11; Neptune.Vx = 1.8271e+03; Neptune.Vy = 4.7731e+03; Neptune.Vz = 1.9082e+03;
Нажмите Reinitialize from Source.
Модель теперь имеет числовые данные, это должно собрать планеты в координатах положения, полученных из баз данных JPL. Однако симуляция модели в этой точке показала бы планеты, перемещающиеся в прямолинейные траектории. Чтобы получить эллиптические орбиты, необходимо завершить модель путем добавления полей тяготения солнца и планеты.

Смоделируйте гравитацию каждого тела солнечной системы с помощью блока Gravitational Field. Этот блок автоматически вычисляет гравитацию тела на всех других телах с помощью закона Ньютона универсальной гравитации.
В каждом диалоговом окне блока Spherical Solid расширьте область Frames и нажмите кнопку Create.
Установите параметр Frame Name на R2 и нажмите кнопку Save. Новая система координат является точной копией системы координат, но имеет отдельный порт системы координат. Можно использовать эти порты, чтобы соединить блоки поля тяготения при предотвращении пересеченных линий связи.
Добавьте в модель девять блоков Gravitational Field из библиотеки Forces и Torques. Блоки предоставляют гравитационным силам, которые каждое тело солнечной системы порождает на все другие тела.
Соедините и назовите блоки как показано в фигуре. Убедитесь, что блоки соединяются непосредственно с блоками Spherical Solid. Такая связь гарантирует, что поля сосредоточены на твердых сферах и жестко соединенные им.
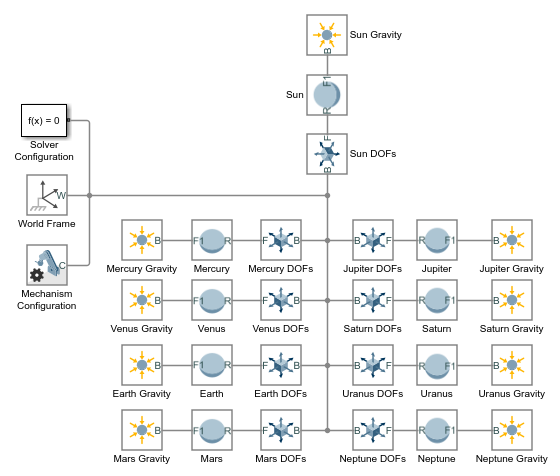
В блоках Поля тяготения задайте параметр Mass как имена полей структуры MATLAB. Введите имена полей в формат Structure.Field, где Structure является именем случая заголовка тела солнечной системы, и Field является строкой M— например, Sun.M или Earth.M. Эти поля были ранее заданы в рабочем пространстве модели.
Сконфигурируйте настройки решателя Simulink®, чтобы получить десять наземных оборотов в одной симуляции. Затем симулируйте модель и просмотрите получившуюся анимацию солнечной системы. Сконфигурируйте настройки анимации, чтобы проигрывать десятилетнюю анимацию в период нескольких секунд.
Откройте Параметры конфигурации. Во вкладке Modeling нажмите Model Settings.
Установите параметр Stop time на 10*365*24*60*60. Этот номер, равный десяти годам в секундах, позволяет вам симулировать все десять земель обороты с 20-го июня 2016 до 20-го июня 2026.
Установите параметр Max step size на 24*60*60. Этот номер, равный одному дню в секундах, мал достаточно, чтобы обеспечить результаты плавной анимации. Увеличьте это число, если вы предпочитаете более быстрые результаты симуляции.
Обновите блок-схему. Во вкладке Modeling нажмите Update Model. Mechanics Explorer открывается статическим 3-D отображением модели в ее начальном состоянии. Проверяйте, что солнце и планеты появляются в панели визуализации и что их относительные размерности и положения разумны.
Запустите симуляцию.. Mechanics Explorer проигрывает анимацию солнечной системы. Обратите внимание на то, что при основной скорости воспроизведения по умолчанию, планеты кажутся статическими. Необходимо увеличить эту скорость в настройках анимации Mechanics Explorer.
В Mechanics Explorer выберите Tools> Animation Settings.
В Base(1X) Playback Speed введите 3153600. Эта скорость соответствует одному наземному обороту каждые десять секунд.
Приостановите и проигрывайте анимацию, чтобы применить новую основную скорость воспроизведения. Рисунок показывает результаты анимации на новой скорости.

Можно открыть полную модель солнечной системы путем ввода smdoc_solar_system_wfield_b в командной строке MATLAB.