Распространено в системе управления использовать выходные параметры инверсной кинематики, чтобы задать сетболы для контроллера. Роботизированная рука, для которой определяют задачу с трассировкой пути с его исполнительным элементом конца, например, может иметь один такой контроллер для каждого соединения. Учитывая путь к трассировке, решатель инверсной кинематики определяет мгновенные углы поворота шарнира, чтобы предназначаться, и от них, диспетчеры могут получить объединенные крутящие моменты приведения в действие, чтобы применяться.
Чтобы поддержать кинематический анализ, требуемый таких задач, Simscape Multibody обеспечивает KinematicsSolver класс. Создайте KinematicsSolver объект получить подходящее представление модели для анализа, затем используйте объектные функции, чтобы сформулировать кинематическую проблему решить. Можно вызвать функции от блока MATLAB function, чтобы включить анализ с симуляцией или из скрипта MATLAB, чтобы запустить анализ вне симуляции.
Рассмотрите sm_import_humanoid_robot_urdf модель от вашей установки Simscape Multibody. Модель имеет робота обхода, спроектированного после человеческого тела. Создайте кинематический объект решателя для модели:
sys = 'sm_import_humanoid_urdf';
ks = simscape.multibody.KinematicsSolver(sys)Объект решателя имеет KinematicsSolver класс и это хранят, среди других данных, переменных вашего анализа. Те переменные могут быть объединенными переменными или структурировать переменные.
Объединенные переменные кодируют состояния соединений — компоненты перевода и вращения последователя относительно базовых систем координат. Переменные системы координат кодируют положение тела, или, более точно, компоненты перевода и вращения системы координат на том теле относительно другой системы координат. Исполнительный элемент конца и системы координат походят на последователя и базовые системы координат соединения.
Перечислите объединенные переменные в своем объекте решателя:
ks.jointVariables
Объединенные переменные включают все присутствующие в модели, когда объект решателя был создан. Если вы обновляетесь, модель — добавляют соединения, говорят — затем необходимо создать новый объект решателя для того, чтобы получить те изменения. Предположим, что ваш анализ ограничивается левой рукой. Соответствующие объединенные переменные являются затем вашим левым запястьем, коленом, лобное плечо, и плечо стреловидные углы — или строки 8, 6, 7 и 2 из объединенной таблицы переменных.
Перечислите переменные системы координат в своем объекте решателя:
ks.frameVariables
Переменные системы координат зависят от выбора исполнительного элемента конца, и этот выбор не может быть определен из одной только вашей модели. Необходимо указать который переменные системы координат использовать. Когда ни один еще не был дан, ни один не существует, чтобы показать.
Позвольте левой руке быть исполнительным элементом конца. Возьмите систему координат F руки, чтобы быть системой координат исполнительного элемента конца и мировой системой координат, чтобы быть вашей системой координат. Можно назвать эти системы координат последователем и основой. Добавьте x, y, и z компоненты перевода, как измерено от основы до последователя, к вашим переменным системы координат:
base = 'sm_import_humanoid_urdf/World/W';
follower = 'sm_import_humanoid_urdf/left_hand/F';
ks.addFrameVariables('Hand', 'translation', base, follower)Обратите внимание на то, что base и follower должны быть полные пути ваших систем координат. Обратите внимание также, что ваши переменные системы координат, как задано, все имеют тип перевода. Что, если вы заботитесь о вращении исполнительного элемента конца также? Можно всегда добавлять (и удалять), переменные системы координат. Добавить x, y, и z компоненты вращения:
ks.addFrameVariables('Hand', 'rotation', base, follower)Hand переменное название группы. Заметьте столбец ID своих таблиц переменных. Все переменные, или систему координат или соединение, называют в формате group.type.component. Первая перечисленная переменная системы координат находится в группе Hand, из типа Translation, и для компонента x. Другими словами, Hand.Translation.x дает x перевод Hand система координат последователя относительно базовой системы координат.
Аналогично, первая объединенная перечисленная переменная принадлежит, чтобы сгруппировать j1, имеет тип Rz, и задает q компонента. Таким образом, j1.Rz.q дает угол поворота (q) из Rz объединенный примитив — или его последователя структурирует относительно его базовой системы координат. Rz шарнирное соединение, примитивное с z для его оси вращения.
Ваше соединение и переменные системы координат теперь достаточны для анализа левой руки. Тип анализа зависит, на которых переменных вы задаете — ваши цели — и какие переменные вы решаете для — ваши выходные параметры. Целевые и выходные переменные могут каждый включить соединение и структурировать переменные. Они - в общем случае, подмножествах всего соединения и структурируют переменные.
Предположим, что вы имеете цели для своих углов поворота шарнира и хотите положение системы координат исполнительного элемента конца. Проблемой является одна из прямой кинематики. Установите объединенные переменные левой руки как ваши цели и переменные системы координат типа перевода как ваш выход:
ks.addTargetVariables(ks.jointVariables.ID([2,6:8])) ks.addOutputVariables(ks.frameVariables.ID(1:3))
Только одна вещь остается, чтобы завершить аналитическую формулировку — численные значения для целевых переменных. Переменные и их модули по умолчанию в градусах. Позвольте левому колену соединиться быть под углом с 30 степенями, левое плечо лобное и левое плечо стреловидные соединения в углу в 45 градусов каждый и соединение левого запястья под углом с 15 степенями:
targets = [30, 45, 45, 15];
Решите для выходных переменных и исследуйте результаты:
outputVec = ks.solve(targets)
outputVec =
0.2120
0.0505
-0.1273outputVec вектор решений для выходных переменных — компоненты перевода, в модуле по умолчанию m, из левой руки система координат F относительно мировой системы координат. Этот вектор отвечает на вопрос, скорее всего, чтобы управлять таким анализом: где исполнительный элемент конца, когда соединения под некоторыми данными углами?
Часто, вы имеете цели для своих переменных системы координат — или своего исполнительного элемента конца — и хотите углы поворота шарнира, сопоставимые с теми целями. Проблемой является теперь одна из инверсной кинематики, и решение, если вы найдены, является вероятным из нескольких возможных. Начните путем очистки целевых и выходных переменных от предыдущих исследований:
ks.clearTargetVariables ks.clearOutputVariables
clearTargetVariables и clearOutputVariables удалите все целевые и выходные переменные из своего объекта решателя. Похожие методы существуют для других переменных. Можно также удалить подмножества переменных. Удалить переменные системы координат типа вращения — строки 4-6 в таблице переменных системы координат:
ks.removeFrameVariables(ks.frameVariables.ID([4:6]))
removeFrameVariables метод удаляет только заданные переменные. Установите свои переменные системы координат как цели и ваши соответствующие объединенные переменные — те из левой руки — как выведено:
ks.addTargetVariables(ks.frameVariables.ID) ks.addOutputVariables(ks.jointVariables.ID([2,6:8]))
Робот мал, и плечи и предплечья - каждый на порядке 8 cm долго. С этой мерой в памяти, устанавливает ваши переменные перевода системы координат на [16, -12, 0] cm, или, в единицах по умолчанию длины, [0.16, -0.12, 0] m. Эти значения относительно лабораторной системы координат, которая расположена в основе головы, с оставленным обращением оси X, обращением оси Y назад и подчеркивающей осью z:
targets = [0.16, -0.12, 0];
Решите для выходных переменных и исследуйте результаты:
outputVec = ks.solve(targets)
outputVec =
52.8406
-108.3936
7.0457
15.0565Выход является теперь вектором углов поворота шарнира в модуле по умолчанию степеней. Углы - каждый для системы координат последователя соединения относительно базовой системы координат. Чтобы интерпретировать углы, это помогает визуализировать модель и проверять ориентацию объединенной базовой системы координат. Можно использовать set_param функция, чтобы включить положение утверждает цели и присваивать расчетные углы соответствующим соединениям:
for i = 1:length(outputVec) path = ks.outputVariables.JointVariableInfo.BlockPath(i); angle = num2str(outputVec(i)); set_param(path, 'PositionTargetSpecify', 'on',... 'PositionTargetValue', angle); end
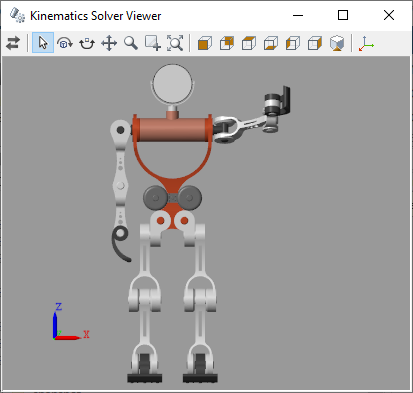
Обновите блок-схему. Во вкладке Modeling нажмите Update Model. Откройте Mechanics Explorer и визуализируйте модель в ее новом начальном состоянии. Рука — исполнительный элемент конца — находится в нужной области кадра, но колено имеет неестественный поворот. Можно откорректировать поворот — или попытаться откорректировать его — путем определения предположений для выходных переменных.
Предположения, сами переменные, служат, чтобы вести решатель к разумной настройке блока. Они могут быть объединенными переменными или структурировать переменные и, в общем случае, соединении обоих. Установите переменную соединения колена — единственное, которому нужно руководство — как переменная предположения:
ks.addInitialGuessVariables(ks.jointVariables.ID(2))
Думайте о переменных предположения как о низкоприоритетных положениях шарниров. Им не всегда удовлетворяют — например, если две переменные предположения находятся в конфликте. Экспериментируйте с предполагаемыми значениями, чтобы найти немного, которые работают. Здесь, чтобы дать колену естественный поворот, это достаточно, чтобы инвертировать знак расчетного угла колена:
guesses = -50;
Решите для выходных переменных с помощью и цели и угадайте переменные, как введено:
outputVec = ks.solve(targets,guesses);
Обновите объединенные цели положения как прежде:
for i = 1:length(outputVec) path = ks.outputVariables.JointVariableInfo.BlockPath(i); angle = num2str(outputVec(i)); set_param(path, 'PositionTargetSpecify', 'on',... 'PositionTargetValue', angle); end
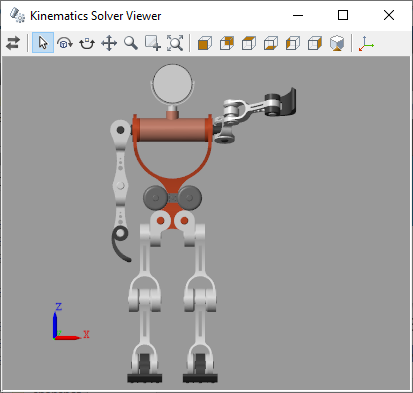
Обновите блок-схему, чтобы визуализировать результаты. Рука должна остаться, где это было с левым коленом, теперь отворачивающимся от туловища.