Inverse Park Transform

Реализация dq0 к abc преобразовывает

Библиотека:
Simscape / Электрический / Управление / Математические Преобразования

Описание

Блок Inverse Park Transform преобразует прямой временной интервал, квадратура и нулевые компоненты во вращающейся системе координат к компонентам трехфазной системы в b a система координат c. Блок может сохранить активные и реактивные мощности со степенями системы во вращающейся системе координат путем реализации инвариантной версии Парка, преобразовывают. Для сбалансированной системы нулевой компонент равен нулю.

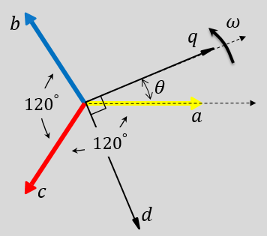
Можно сконфигурировать блок, чтобы выровнять a - ось трехфазной системы или к d - или к q - ось вращающейся системы координат во время, t = 0. Рисунки показывают направление магнитных осей обмоток статора в b a система координат c и вращающийся d-q система координат где:

a - ось и q - ось первоначально выравниваются.
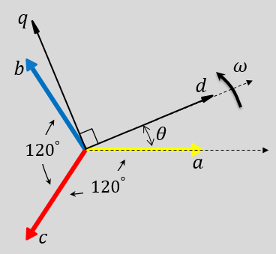
a - ось и d - ось первоначально выравниваются.

В обоих случаях, угол θ = ω t, где

θ является углом между a и осями q для q - выравниванием оси или углом между a и осями d для d - выравнивание оси.
ω является скоростью вращения d-q система координат.
t является временем, в s, от начального выравнивания.

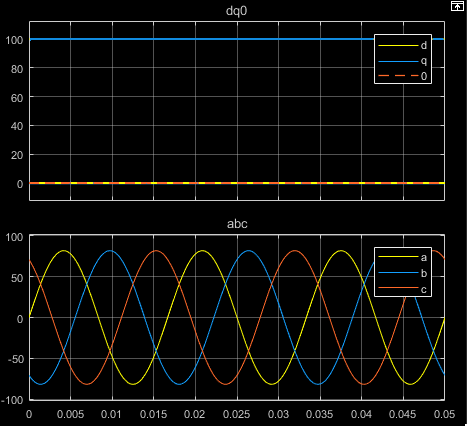
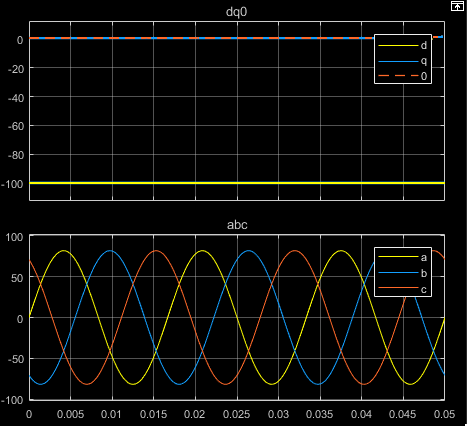
Рисунки показывают ответ времени отдельных компонентов эквивалентного сбалансированного dq0 и abc для:

Выравнивание a - вектора фазы к q - ось
Выравнивание a - вектора фазы к d - ось

Определение уравнений

Блок Inverse Park Transform реализует преобразование для a - фазы к q - выравнивание оси как

$[\begin{matrix} a \\ b \\ c \end{matrix}] = [\begin{matrix} sin (θ) & потому что (θ) & 1 \\ sin (θ - \frac{2 π}{3}) & потому что (θ - \frac{2 π}{3}) & 1 \\ sin (θ + \frac{2 π}{3}) & потому что (θ + \frac{2 π}{3}) & 1 \end{matrix}] [\begin{matrix} d \\ q \\ 0 \end{matrix}],$

где:

d и q являются компонентами 2D системы координат во вращающейся системе координат.
a, b и c являются компонентами трехфазной системы в b a система координат c.
0 является нулевым компонентом 2D системы координат в стационарной системе координат.

Для инварианта степени a - фаза к q - выравнивание оси, блок реализует преобразование с помощью этого уравнения:

$[\begin{matrix} a \\ b \\ c \end{matrix}] = \sqrt{\frac{2}{3}} [\begin{matrix} sin (θ) & потому что (θ) & \sqrt{\frac{1}{2}} \\ sin (θ - \frac{2 π}{3}) & потому что (θ - \frac{2 π}{3}) & \sqrt{\frac{1}{2}} \\ sin (θ + \frac{2 π}{3}) & потому что (θ + \frac{2 π}{3}) & \sqrt{\frac{1}{2}} \end{matrix}] [\begin{matrix} d \\ q \\ 0 \end{matrix}] .$

Для a - фазы к d - выравнивание оси, блок реализует преобразование с помощью этого уравнения:

$[\begin{matrix} a \\ b \\ c \end{matrix}] = [\begin{matrix} потому что (θ) & - sin (θ) & 1 \\ потому что (θ - \frac{2 π}{3}) & - sin (θ - \frac{2 π}{3}) & 1 \\ потому что (θ + \frac{2 π}{3}) & - sin (θ + \frac{2 π}{3}) & 1 \end{matrix}] [\begin{matrix} d \\ q \\ 0 \end{matrix}] .$

Блок реализует инвариант степени a - фаза к d - выравнивание оси как

$[\begin{matrix} a \\ b \\ c \end{matrix}] = \sqrt{\frac{2}{3}} [\begin{matrix} потому что (θ) & - sin (θ) & \sqrt{\frac{1}{2}} \\ потому что (θ - \frac{2 π}{3}) & - sin (θ - \frac{2 π}{3}) & \sqrt{\frac{1}{2}} \\ потому что (θ + \frac{2 π}{3}) & - sin (θ + \frac{2 π}{3}) & \sqrt{\frac{1}{2}} \end{matrix}] [\begin{matrix} d \\ q \\ 0 \end{matrix}] .$

Порты

Входной параметр

развернуть все

`dq0` — d-q ось и нулевые компоненты
вектор

Прямая ось и компоненты квадратурной оси и нулевой компонент системы во вращающейся системе координат.

Типы данных: single | double

`_θabc` — Вращательный угол
скаляр | в радианах

Угловое положение вращающейся системы координат. Значение этого параметра равно полярному расстоянию от вектора a - фаза в системе координат abc к первоначально выровненной оси системы координат dq0.

Типы данных: single | double

Вывод

развернуть все

`abc` — a - b - и c - компоненты фазы
вектор

Компоненты трехфазной системы в системе координат abc.

Типы данных: single | double

Параметры

развернуть все

`Power Invariant` — Инвариант степени преобразовывает
от (значения по умолчанию) | на

Опция, чтобы сохранить активную и реактивную мощность b a система координат c.

`Phase-a axis alignment` — выравнивание системы координат dq0
`Q-axis` (значение по умолчанию) | `D-axis`

Выровняйте a - вектор фазы системы координат abc к d - или q - ось вращающейся системы координат.

Примеры модели

Электродвигатель Dyno

Смоделируйте тест динамометра электромобиля. Тестовая среда содержит асинхронную машину (ASM) и внутренний постоянный магнит синхронную машину (IPMSM), соединенный спина к спине через механический вал. Обе машины питаются высоковольтными батареями через управляемые трехфазные конвертеры. ASM на 164 кВт производит крутящий момент загрузки. IPMSM на 35 кВт является электрической машиной под тестом. Машина Управления Под Тестом (IPMSM) подсистема управляет крутящим моментом IPMSM. Контроллер включает многоскоростную основанную на PI управляющую структуру. Уровень управления крутящим моментом разомкнутого цикла медленнее, чем уровень текущего управления с обратной связью. Планирование задач для контроллера реализовано как конечный автомат Stateflow®. Машина Загрузки Управления (ASM) подсистема использует один уровень, чтобы контролировать скорость ASM. Подсистема Визуализации содержит осциллографы, которые позволяют вам видеть результаты симуляции.

Документация

Inverse Park Transform

Описание

Определение уравнений

Порты

Входной параметр

dq0 — d-q ось и нулевые компоненты вектор

θabc — Вращательный угол скаляр | в радианах

Вывод

abc — a - b - и c - компоненты фазы вектор

Параметры

Power Invariant — Инвариант степени преобразовывает от (значения по умолчанию) | на

Phase-a axis alignment — выравнивание системы координат dq0 Q-axis (значение по умолчанию) | D-axis

Примеры модели

Электродвигатель Dyno

Энергетический баланс в 48-вольтовом генераторе начинающего

Управление крутящим моментом HESM

Скоростное управление HESM

Стабилизация напряжения IPMSG

Управление крутящим моментом IPMSM в параллельном HEV

Управление крутящим моментом IPMSM в ряду HEV

Управление крутящим моментом IPMSM в последовательно-параллельном HEV

Управление крутящим моментом IPMSM в Диске оси HEV

Скоростное управление IPMSM

Управление крутящим моментом SM

Скоростное управление SM

Синхронное скоростное управление машиной нежелания

Трехфазный асинхронный диск с управлением датчиком

Трехфазный асинхронный диск с управлением Sensorless

Ссылки

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Блоки

Введенный в R2017b

Документация Simscape Electrical

Поддержка

`dq0` — d-q ось и нулевые компоненты
вектор

`_θabc` — Вращательный угол
скаляр | в радианах

`abc` — a - b - и c - компоненты фазы
вектор

`Power Invariant` — Инвариант степени преобразовывает
от (значения по умолчанию) | на

`Phase-a axis alignment` — выравнивание системы координат dq0
`Q-axis` (значение по умолчанию) | `D-axis`

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.