В приложениях робототехники много различных систем координат могут использоваться, чтобы задать, где роботы, датчики и другие объекты расположены. В общем случае местоположение объекта в трехмерном пространстве может быть задано значениями ориентации и положением. Существует несколько возможных представлений для этих значений, некоторые из которых характерны для определенных приложений. Перевод и вращение являются альтернативными условиями для положения и ориентации. Robotics System Toolbox™ поддерживает представления, которые обычно используются в робототехнике, и позволяет вам преобразовывать между ними. Можно преобразовать между системами координат, когда вы применяете эти представления 3-D точкам. Эти поддерживаемые представления детализированы ниже с краткими объяснениями их использования и числового эквивалента в MATLAB®. Каждое представление имеет сокращение от своего имени. Это используется в именовании аргументов и функций преобразования, которые поддерживаются в этом тулбоксе.
В конце этого раздела можно узнать о функциях преобразования, что мы предлагаем преобразовывать между этими представлениями.
Robotics System Toolbox принимает, что положения и ориентации заданы в предназначенной для правой руки Декартовой системе координат.
Сокращение: axang
Вращение в трехмерном пространстве, описанном скалярным вращением вокруг фиксированной оси, задано вектором.
Числовое Представление: 1 3 единичный вектор и скалярный угол, объединенный как вектор 1 на 4
Например, вращение pi/2 радианы вокруг y - ось были бы:
axang = [0 1 0 pi/2]
Сокращение: eul
Углы Эйлера являются тремя углами, которые описывают ориентацию твердого тела. Каждый угол является скалярным вращением вокруг данной координатной оси системы координат. Robotics System Toolbox поддерживает два порядка вращения. 'ZYZ' порядок оси обычно используется в приложениях робототехники. Мы также поддерживаем 'ZYX' порядок оси, который также обозначен как “Отклонение от курса Подачи списка (rpy)”. Знание, какой порядок оси вы используете, важно для, применяют вращение к точкам и в преобразовании в другие представления.
Числовое Представление: 1 3 вектор скалярных углов
Например, вращение вокруг y - ось пи было бы выражено как:
eul = [0 pi 0]
Примечание: порядок оси не хранится в преобразовании, таким образом, необходимо знать о том, какой порядок вращения состоит в том, чтобы быть применен.
Сокращение: tform
Гомогенная матрица преобразования комбинирует перевод и вращение в одну матрицу.
Числовое Представление: матрица 4 на 4
Например, вращение угла α вокруг y - оси и перевода 4 модулей вдоль y - ось было бы выражено как:
tform = cos α 0 sin α 0 0 1 0 4 -sin α 0 cos α 0 0 0 0 1
Необходимо предварительно умножить матрицу преобразования с однородными координатами, которые представлены как матрица векторов-строк (n-by-4 матрица точек). Используйте транспонирование (') вращать ваши точки для умножения матриц. Например:
points = rand(100,4); tformPoints = (tform*points')';
Сокращение: quat
Кватернион является четырехэлементным вектором со скалярным вращением и вектором с 3 элементами. Кватернионы выгодны, потому что они избегают проблем сингулярности, которые свойственны от других представлений. Первым элементом, w, является скаляр, чтобы нормировать вектор с тремя другими значениями, [x y z], задающий ось вращения.
Числовое Представление: вектор 1 на 4
Например, вращение pi/2 вокруг y - ось была бы выражена как:
quat = [0.7071 0 0.7071 0]
Сокращение: rotm
Матрица вращения описывает вращение в трехмерном пространстве. Это - квадратная, ортонормированная матрица с определителем 1.
Числовое Представление: 3х3 матрица
Например, вращение α степеней вокруг x - ось было бы:
rotm =
1 0 0
0 cos α -sin α
0 sin α cos αНеобходимо предварительно умножить матрицу вращения с координатами, которые представлены как матрица векторов-строк (n-by-3 матрица точек). Используйте транспонирование (') вращать ваши точки для умножения матриц. Например:
points = rand(100,3); rotPoints = (rotm*points')';
Сокращение: trvec
Вектор сдвига представлен в 3-D Евклидово пространстве как Декартовы координаты. Это только включает координатный перевод, примененный одинаково ко всем точкам. Нет никакого включенного вращения.
Числовое Представление: 1 3 вектор
Например, перевод 3 модулями вдоль x - осью и 2,5 модулями вдоль z - ось был бы выражен как:
trvec = [3 0 2.5]
Robotics System Toolbox обеспечивает функции преобразования для ранее упомянутых представлений преобразования. Не все преобразования поддерживаются специализированной функцией. Ниже таблица, показывающая, какие преобразования поддерживаются (в синем). Сокращения от представлений вращения и перевода показывают также.
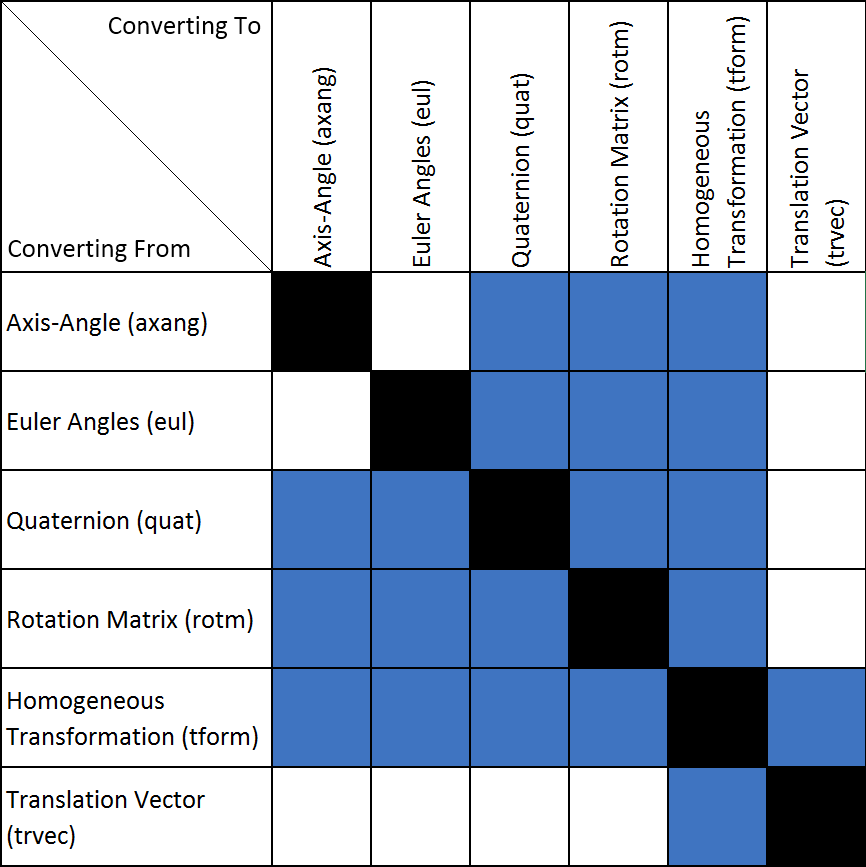
Имена всех функций преобразования следуют за стандартным форматом. Они следуют за формой alpha2beta где alpha сокращение от того, что вы преобразуете от и beta то, во что вы преобразуете как сокращение. Например, преобразованием от Углов Эйлера до кватерниона был бы eul2quat.
Все функции ожидают допустимые входные параметры. Если вы зададите недопустимые входные параметры, выходные параметры будут не определены.
Существуют другие функции преобразования для преобразования между радианами и степенями, Декартовыми и однородными координатами, и для вычисления перенесенных угловых различий. Для полного списка преобразований смотрите Координатные Преобразования и Траектории.