Как преобразование Фурье, непрерывный вейвлет преобразовывает (CWT) использует скалярные произведения, чтобы измерить подобие между сигналом и функцией анализа. В преобразовании Фурье функции анализа являются комплексными экпонентами, . Получившееся преобразование является функцией одной переменной, ω. В кратковременном преобразовании Фурье функции анализа являются оконными комплексными экпонентами, , и результатом является функция двух переменных. Коэффициенты STFT, представляйте соответствие между сигналом и синусоидой с угловой частотой ω в интервале заданной длины, сосредоточенной в τ.
В CWT функция анализа является вейвлетом, ψ. CWT сравнивает сигнал с переключенными и сжатыми или расширенными версиями вейвлета. Протяжение или сжатие функции коллективно упоминаются как расширение или масштабирование и соответствуют физическому понятию шкалы. Путем сравнения сигнала с вейвлетом в различных шкалах и положениях, вы получаете функцию двух переменных. 2D представление 1D сигнала избыточно. Если вейвлет с комплексным знаком, CWT является комплексной функцией шкалы и положения. Если сигнал с действительным знаком, CWT является действительной функцией шкалы и положения. Для масштабного коэффициента, a> 0, и положение, b, CWT:
где обозначает сопряженное комплексное число. Не только делают значения шкалы и положения влияют на коэффициенты CWT, выбор вейвлета также влияет на значения коэффициентов.
Путем непрерывного варьирования значений масштабного коэффициента, a, и параметра положения, b, вы получаете cwt коэффициенты C(a,b). Обратите внимание на то, что для удобства, зависимость коэффициентов CWT на функции и вейвлете анализа была подавлена.
Умножение каждого коэффициента соответственно масштабированным и переключенным вейвлетом дает к составляющим вейвлетам исходного сигнала.
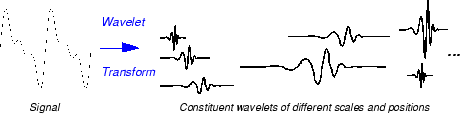
Существует много различных допустимых вейвлетов, которые могут использоваться в CWT. В то время как это может казаться сбивающим с толку, что существует столько вариантов для вейвлета анализа, это - на самом деле сила анализа вейвлета. В зависимости от того, какие функции сигнала вы пытаетесь обнаружить, вы свободны выбрать вейвлет, который упрощает ваше обнаружение той функции. Например, при попытке обнаружить резкие разрывы в своем сигнале, можно выбрать один вейвлет. С другой стороны, если вы интересуетесь нахождением колебаний со сглаженными началами и смещений, вы свободны выбрать вейвлет, который более тесно совпадает с тем поведением.
Как концепция частоты, шкала является другим полезным свойством сигналов и изображений. Например, можно анализировать температурные данные для изменений по различным шкалам. Можно посмотреть на изменения от десятилетия к десятилетию или ежегодный. Конечно, можно исследовать более прекрасные (ежедневные), или более грубые изменения шкалы также. Некоторые процессы показывают интересные изменения на долгом времени или пространственные шкалы, которые не очевидны на маленьком времени или пространственных шкалах. Противоположная ситуация также происходит. Некоторые наши перцепционные способности показывают масштабную инвариантность. Вы распознаете людей, которых вы знаете независимо от того, смотрите ли вы на большой портрет или маленькую фотографию.
Чтобы пойти вне разговорных описаний, таких как “протяжение” или “уменьшение”, мы вводим масштабный коэффициент, часто обозначаемый буквой a. Масштабным коэффициентом является по сути положительное количество, a> 0. Для синусоид эффект масштабного коэффициента очень легко видеть.
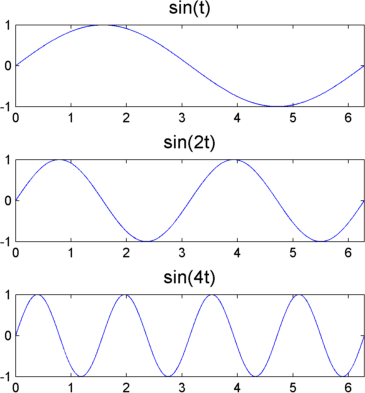
В sin (в) шкала является инверсией частоты радиана, a.
Масштабный коэффициент работает точно то же самое с вейвлетами. Чем меньший масштабный коэффициент, тем более “сжатый” вейвлет. С другой стороны, чем больше шкала, тем более расширенный вейвлет. Следующая фигура иллюстрирует это для вейвлетов в шкалах 1,2, и 4.
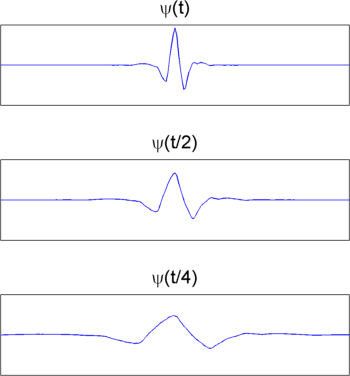
Эта общая обратная связь между шкалой и частотой содержит для сигналов в целом.
Мало того, что представление масштаба времени является различным способом просмотреть данные, это - очень естественный способ просмотреть данные, выведенные из большого количества природных явлений.
Существует ясно отношение между шкалой и частотой. Вспомните, что более длинные шкалы соответствуют наиболее “расширенным” вейвлетам. Чем более расширенный вейвлет, тем дольше фрагмент сигнала, с которым это сравнивается, и поэтому более грубое функции сигнала, измеренные коэффициентами вейвлета.

Подводя итоги, общее соответствие между шкалой и частотой:
Мелкомасштабный a ⇒ Сжатый вейвлет ⇒ Быстро изменяющиеся детали ⇒ Высокая частота ω.
Долго масштабируйте a ⇒ Расширенный вейвлет ⇒ Медленно изменение, неровности ⇒ Низкая частота ω.
В то время как существует общее отношение между шкалой и частотой, никакое точное отношение не существует. Пользователи, знакомые с анализом Фурье часто, хотят задать отображение между вейвлетом в данной шкале с заданным периодом выборки к частоте в герц. Можно только сделать это в общем смысле. Поэтому лучше говорить о псевдочастоте, соответствующей шкале. Программное обеспечение Wavelet Toolbox™ предоставляет двум функциям centfrq и scal2frq, которые позволяют вам найти эти аппроксимированные отношения частоты шкалы для заданных вейвлетов и шкал.
Основной подход идентифицирует пиковую мощность в преобразовании Фурье вейвлета как его центральная частота и делит то значение на продукт шкалы и интервала выборки. Смотрите scal2frq для деталей. Следующий пример показывает соответствие между предполагаемой центральной частотой db8 вейвлет и синусоида той же частоты.
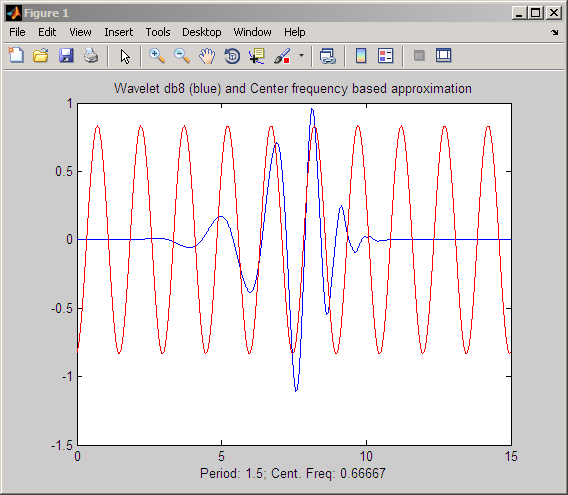
Отношение между шкалой и частотой в CWT также исследуется в Непрерывном Преобразовании Вейвлета как Полосовой фильтр.
Сдвиг вейвлета просто означает задерживаться (или совершенствоваться) его начало. Математически, задержка функции f (t) k представлена f (t – k):
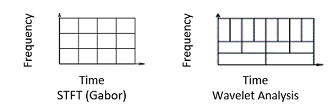
В Кратковременном преобразовании Фурье STFT описан как работа с окнами сигнала создать локальный анализ частоты. Недостаток подхода STFT - то, что размер окна является постоянным. Существует компромисс в выборе размера окна. Более длинное окно времени улучшает разрешение частоты при приведении к более плохому разрешению времени, потому что преобразование Фурье теряет все разрешение времени по длительности окна. С другой стороны более короткое окно времени улучшает локализацию времени при приведении к более плохому разрешению частоты.
Анализ вейвлета представляет следующий логический шаг: метод работы с окнами с областями переменного размера. Анализ вейвлета позволяет использование долговременных интервалов, где вы хотите более точную низкочастотную информацию и более короткие области, где вы хотите высокочастотную информацию.

Следующая фигура контрастирует различные способы, которыми STFT и анализ вейвлета анализируют плоскость частоты времени.