Этот раздел берет вас через функции 2D дискретного анализа вейвлета с помощью программного обеспечения Wavelet Toolbox™. Тулбокс обеспечивает эти функции для анализа изображения. Для получения дополнительной информации смотрите страницы ссылки на функцию.
В этом разделе представление и примеры используют 2D массивы, соответствующие индексируемым представлениям изображений. Однако описанные функции также доступны при использовании изображений истинного цвета, которые представлены m- n- 3 массива uint8. Для получения дополнительной информации о форматах изображения смотрите Вейвлеты: Работа с Изображениями.
FunctionName | Цель |
|---|---|
Шумоподавление вейвлета изображений | |
Обеспечьте значения по умолчанию для шумоподавления и сжатия | |
Оштрафованный порог для вейвлета 1D или 2D шумоподавление | |
Пороги для вейвлета 2D использование стратегия Birgé-Massart | |
Шумоподавление вейвлета и сжатие | |
Пороговый менеджер по настройкам |
В этом разделе вы будете учиться
Как загрузить изображение
Как анализировать изображение
Как выполнить одноуровневые и многоуровневые разложения изображений и реконструкции (только командная строка)
Как использовать функции режима Square и Tree (только графический интерфейс пользователя)
Как увеличить масштаб детали (только графический интерфейс пользователя)
Как сжать изображение
В этом примере показано, как можно использовать 2D анализ вейвлета, чтобы сжать изображение эффективно, не жертвуя его ясностью.
Примечание: Вместо того, чтобы непосредственно использовать image(I) визуализировать изображение I, мы используем image(wcodemat(I)), который отображает перемасштабированную версию I продвижение к более ясному представлению деталей и приближениям (см. wcodemat).
Загрузите изображение.
load wbarb whos X map
Name Size Bytes Class Attributes X 256x256 524288 double map 192x3 4608 double
Отобразите изображение.
image(X) colormap(map) colorbar

Если палитра является гладкой, вейвлет преобразовывают, может быть непосредственно применен к индексируемому изображению; в противном случае индексируемое изображение должно быть преобразовано в полутоновый формат. Для получения дополнительной информации смотрите Вейвлеты: Работа с Изображениями. Поскольку палитра является гладкой в этом изображении, можно теперь выполнить разложение.
Выполните одноуровневое разложение вейвлета изображения с помощью bior3.7 вейвлет. Матрица коэффициентов cA1 коэффициенты приближения. Горизонталь, вертикальные, и диагональные детали находятся в матрицах cH1, cV1, и cD1, соответственно.
wv = 'bior3.7';
[cA1,cH1,cV1,cD1] = dwt2(X,wv);Используйте idwt1 создать приближения и детали от коэффициентов. (Примечание: можно также использовать upcoef2.
sx = size(X); A1 = idwt2(cA1,[],[],[],wv,sx); H1 = idwt2([],cH1,[],[],wv,sx); V1 = idwt2([],[],cV1,[],wv,sx); D1 = idwt2([],[],[],cD1,wv,sx);
Отобразите приближения и детали.
figure subplot(2,2,1) image(wcodemat(A1,192)) title('Approximation A1') subplot(2,2,2) image(wcodemat(H1,192)) title('Horizontal Detail H1') subplot(2,2,3) image(wcodemat(V1,192)) title('Vertical Detail V1') subplot(2,2,4) image(wcodemat(D1,192)) title('Diagonal Detail D1') colormap(map)

Регенерируйте изображение одноуровневым обратным дискретным вейвлетом, преобразовывают. Подтвердите, что различие между регенерированными и оригинальными изображениями мало.
Xrec = idwt2(cA1,cH1,cV1,cD1,wv); max(abs(X(:)-Xrec(:)))
ans = 1.4211e-13
Выполните разложение вейвлета уровня 2 изображения с помощью того же bior3.7 вейвлет. Коэффициенты всех компонентов разложения второго уровня (то есть, приближения второго уровня и первых двух уровней детализации) возвращены конкатенированные в один вектор, CАргументы бухгалтерская матрица, которая отслеживает размеры каждого компонента.
[c,s] = wavedec2(X,2,wv);
Извлеките коэффициенты приближения уровня 2. Извлеките первое - и коэффициенты детали второго уровня.
cA2 = appcoef2(c,s,wv,2); [cH2,cV2,cD2] = detcoef2('all',c,s,2); [cH1,cV1,cD1] = detcoef2('all',c,s,1);
Восстановите приближение уровня 2 и детали уровня 1 и уровня 2.
A2 = wrcoef2('a',c,s,wv,2); H1 = wrcoef2('h',c,s,wv,1); V1 = wrcoef2('v',c,s,wv,1); D1 = wrcoef2('d',c,s,wv,1); H2 = wrcoef2('h',c,s,wv,2); V2 = wrcoef2('v',c,s,wv,2); D2 = wrcoef2('d',c,s,wv,2);
Отобразите приближение и детали.
figure subplot(2,4,1) image(wcodemat(A1,192)) title('Approximation A1') subplot(2,4,2) image(wcodemat(H1,192)) title('Horizontal Detail H1') subplot(2,4,3) image(wcodemat(V1,192)) title('Vertical Detail V1') subplot(2,4,4) image(wcodemat(D1,192)) title('Diagonal Detail D1') subplot(2,4,5) image(wcodemat(A2,192)) title('Approximation A2') subplot(2,4,6) image(wcodemat(H2,192)) title('Horizontal Detail H2') subplot(2,4,7) image(wcodemat(V2,192)) title('Vertical Detail V2') subplot(2,4,8) image(wcodemat(D2,192)) title('Diagonal Detail D2') colormap(map)

Сожмите изображение. Используйте ddencmp вычислить параметры по умолчанию и wdencmp выполнять фактическое сжатие.
[thr,sorh,keepapp] = ddencmp('cmp','wv',X); [Xcomp,CXC,LXC,PERF0,PERFL2] = ... wdencmp('gbl',c,s,wv,2,thr,sorh,keepapp);
Сравните сжатое изображение с оригинальным изображением.
fprintf('Percentage of wavelet coefficients set to zero: %.4f\nPercentage of energy preserved: %.4f\n',... PERF0,PERFL2);
Percentage of wavelet coefficients set to zero: 49.8024 Percentage of energy preserved: 99.9817
figure subplot(121) image(X) title('Original Image') axis square subplot(122) image(Xcomp) title('Compressed Image') axis square colormap(map)

Обратите внимание на то, что, даже при том, что сжатое изображение создается только из приблизительно вдвое меньше ненулевых коэффициентов вейвлета, чем оригинал, в качестве изображения нет почти никакого обнаруживаемого ухудшения.
В этом разделе мы исследуем то же изображение как в предыдущем разделе, но мы используем приложение Wavelet Analyzer, чтобы анализировать изображение.
Запустите 2D аналитический инструмент вейвлета.
От подсказки MATLAB® введите waveletAnalyzer.
Главное меню Инструмента Вейвлета появляется.
Кликните по пункту меню Wavelet 2-D. Дискретный аналитический инструмент вейвлета для 2D данных изображения появляется.
Загрузите изображение.
В командной строке MATLAB ввести
load wbarb
X переменная. Нажмите ОК, чтобы импортировать изображение.Изображение загружается в инструмент Wavelet 2-D.
Анализируйте изображение.
Используя меню Wavelet и Level, расположенные к верхнему правому углу, определите семейство вейвлетов, тип вейвлета и количество уровней, которые будут использоваться в анализе.
Для этого анализа выберите bior3.7 вейвлет на уровне 2.
Нажмите кнопку Analyze. После паузы для расчета инструмент Wavelet 2-D отображает свой анализ.
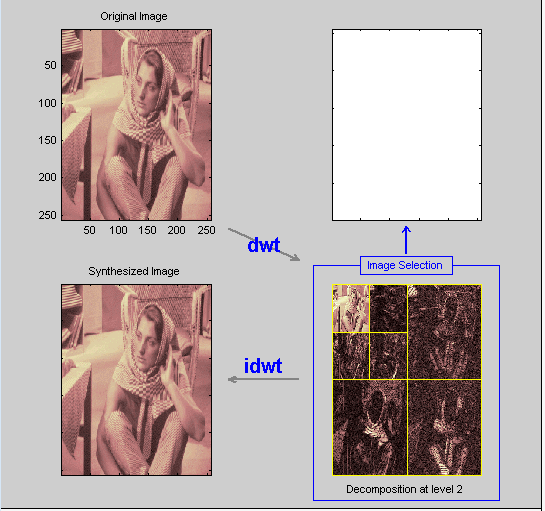
Использование квадратных функций режима
По умолчанию анализ появляется в “Квадратном Режиме”. Этот режим включает четыре различных отображения. В верхнем левом углу оригинальное изображение. Ниже этого изображение, восстановленное от различных приближений и деталей. К нижнему правому углу разложение, показывающее самые грубые коэффициенты приближения и всю горизонталь, диагональ и вертикальные коэффициенты детали. Наконец, пробел визуализации в правых верхних отображениях любой компонент анализа, на который вы хотите посмотреть более тесно.
Нажмите на любой компонент разложения в нижнем правом окне.
Синяя граница подсвечивает выбранный компонент. В нижнем правом углу окна Wavelet 2-D существует набор трех кнопок, пометил “Operations on selected image”. Обратите внимание на то, что, если вы щелкнете еще раз по тому же компоненту, вы отмените выбор его, и синяя граница исчезает.
Нажмите кнопку Visualize.
Выбранное изображение отображено в области визуализации. Вы видите сырые данные, неисправимые 2D коэффициенты вейвлета. Используя другие кнопки, можно отобразить восстановленную версию выбранного компонента изображения, или можно просмотреть выбранный компонент в полноэкранном разрешении.
Использование древовидных функций режима
Выберите Tree из меню View Mode.
Ваше отображение изменяется, чтобы показать следующее.
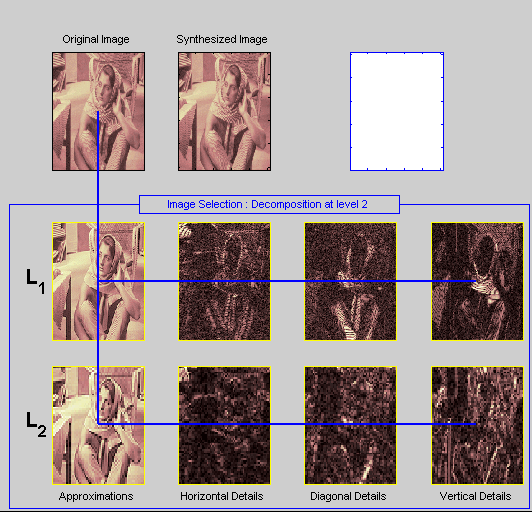
Это - та же информация, показанная в квадратном режиме, с, кроме того, всеми коэффициентами приближения, но расположенный, чтобы подчеркнуть древовидную структуру разложения. Различные кнопки и меню работают все равно, как они делают в квадратном режиме.
Увеличивание масштаб детали
Перетащите поле круглой резинки (удержанием левой кнопки мыши) по фрагменту изображения, которое вы хотите увеличить.
Нажмите кнопку XY + (расположенный внизу экрана), чтобы масштабировать горизонтально и вертикально.
![]()
Инструмент Wavelet 2-D увеличивает отображенные изображения.
Чтобы масштабировать назад к исходному увеличению, нажмите History <<-кнопка.
Нажмите кнопку Compress, расположенную к верхнему правому углу окна Wavelet 2-D. Окно Wavelet 2-D Compression появляется.
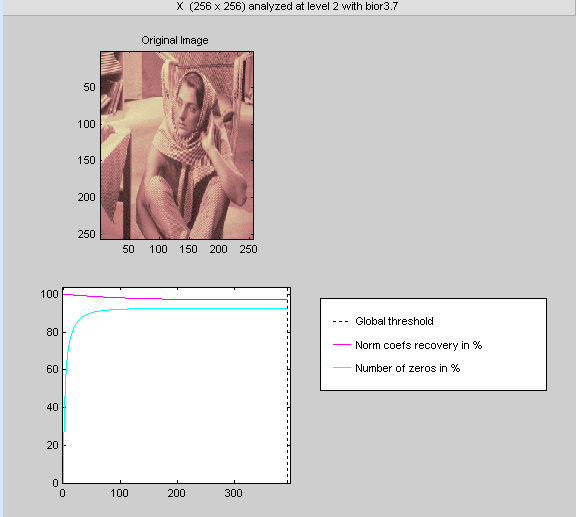
Инструмент автоматически выбирает уровни пороговой обработки, чтобы обеспечить, хороший начальный баланс между сохранением энергии изображения при минимизации количества коэффициентов должен был представлять изображение.
Однако можно также настроить пороги вручную с помощью опцией пороговой обработки Уровня, и затем ползунками или редактированиями, соответствующими каждому уровню.
В данном примере выберите опцией пороговой обработки Уровня и выберите Remove около 0 методов в Избранном меню метода задания порога.
Следующее окно отображено.
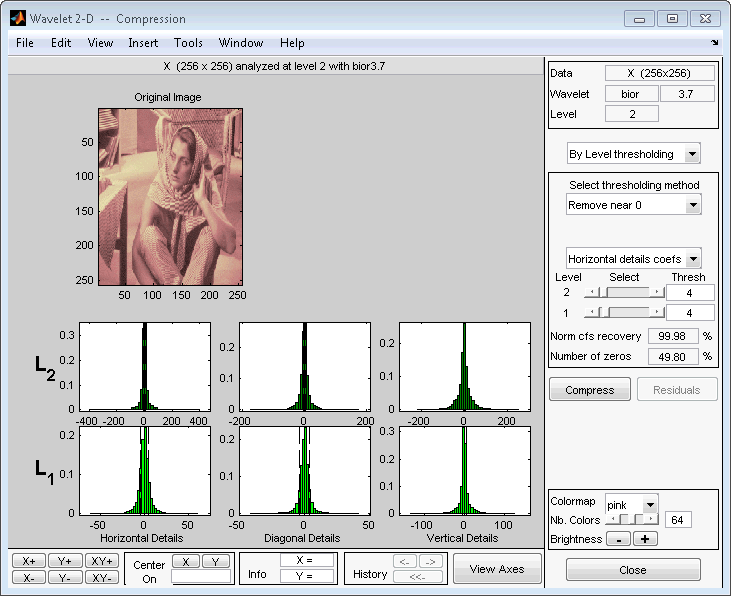
Выберите из меню направления, хотите ли вы настроить пороги для горизонтали, диагональных или вертикальных деталей. Чтобы внести фактические корректировки для каждого уровня, используйте ползунки или используйте левую кнопку мыши, чтобы непосредственно перетащить пунктирные линии.
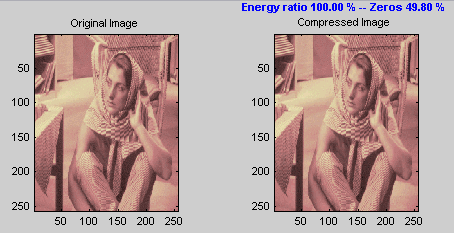
Чтобы сжать оригинальное изображение, нажмите кнопку Compress. После паузы для расчета сжатое изображение отображено около оригинала. Заметьте, что сжатие устраняет почти половину коэффициентов, все же никакое обнаруживаемое ухудшение изображения не появляется.
Покажите остаточные значения.
От инструмента Wavelet 2-D Compression нажмите кнопку Residuals. Окно More on Residuals for Wavelet 2-D Compression появляется.
Отображенные статистические данные включают меры тенденции (среднее значение, режим, медиана) и дисперсия (область значений, стандартное отклонение). Кроме того, инструмент предоставляет схемы плотности распределения (гистограммы и совокупные гистограммы). Тот же инструмент существует для инструмента Wavelet 2-D Denoising.
Статистические данные, отображенные в вышеупомянутой фигуре, связаны с отображенным изображением, но не с исходным. Обычно этой информацией является то же самое, но в некоторых случаях, краевые эффекты могут заставить оригинальное изображение быть обрезанным немного. Чтобы видеть точную статистику, используйте функции командной строки, чтобы получить желаемое изображение и затем применить желаемый MATLAB статистическая функция (функции).
2D графический инструмент Вейвлета позволяет вам импортировать информацию из и экспортировать информацию в диск, если вы придерживаетесь соответствующих форматов файлов.
Можно сохранить синтезируемые образы, коэффициенты и разложения от инструмента Wavelet 2-D до диска, где информацией можно управлять и позже повторно импортировать в графический инструмент.
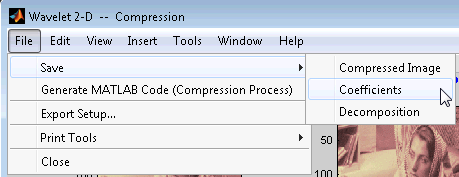
Сохранение Синтезируемых Образов. Можно обработать изображение в инструменте Wavelet 2-D, и затем сохранить обработанный образ к MAT-файлу (с дополнительным mat или другой).
Например, загрузите анализ в качестве примера:
Файл> Анализ В качестве примера> Индексируемые Изображения> на уровне 3, с Детайлем Дюрером sym4
и выполните сжатие на оригинальном изображении. Когда вы закрываете окно Wavelet 2-D Compression, обновляете синтезируемое изображение путем нажимания кнопку Да в диалоговом окне, которое появляется.
Затем от инструмента Wavelet 2-D выберите пункт меню File> Save> Synthesized Image. Диалоговое окно кажется позволяющим вам, чтобы выбрать папку и имя файла для MAT-файла (с дополнительным mat или другой). В данном примере выберите имя symage.
Чтобы загрузить изображение в вашу рабочую область, ввести
load symage whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 359x371 | 1065512 | double array |
map | 64x3 | 1536 | double array |
valTHR | 1x1 | 8 | double array |
wname | 1x4 | 8 | char array |
Синтезируемое изображение дано X и map содержит палитру. Кроме того, параметры процесса шумоподавления или сжатия даны именем вейвлета (wname) и глобальный порог (valTHR).
Сохранение Дискретных Коэффициентов Преобразования Вейвлета. Инструмент Wavelet 2-D позволяет вам сохранить коэффициенты дискретного вейвлета преобразовывает (DWT) к диску. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете.
Чтобы избавить коэффициенты DWT от существующего анализа, используйте пункт меню File> Save> Coefficients.
Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения коэффициентов.
Рассмотрите анализ в качестве примера:
Файл> Анализ В качестве примера> Индексируемые Изображения> на уровне 3, с Детайлем Дюрером sym4
После сохранения дискретных коэффициентов вейвлета к файлу cfsdurer.mat, загрузите переменные в свою рабочую область:
load cfsdurer whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x142299 | 1138392 | double array |
map | 64x3 | 1536 | double array |
sizes | 5x2 | 80 | double array |
valTHR | 0x0 | 0 | double array |
wname | 1x4 | 8 | char array |
Переменный map содержит палитру. Переменный wname содержит имя вейвлета и valTHR пусто, поскольку синтезируемое изображение совпадает с исходным.
Переменные coefs и sizes содержите дискретные коэффициенты вейвлета и связанные матричные размеры. Более точно, в вышеупомянутом примере, coefs 1 142299 вектор конкатенированных коэффициентов и sizes дает длину каждого компонента.
Сохранение Разложений. Инструмент Wavelet 2-D позволяет вам сохранить целый набор данных от дискретного анализа вейвлета до диска. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете, сопровождаемый дополнительным wa2 (2D анализ вейвлета).
Откройте инструмент Wavelet 2-D и загрузите анализ в качестве примера:
Файл> Анализ В качестве примера> Индексируемые Изображения> на уровне 3, с Детайлем Дюрером sym4 .
Чтобы сохранить данные от этого анализа, используйте пункт меню File> Save> Decomposition.
Диалоговое окно появляется, который позволяет вам задать папку и имя файла для того, чтобы хранить данные о разложении. Введите имя decdurer.
После сохранения данных о разложении к файлу decdurer.wa2, загрузите переменные в свою рабочую область:
load decdurer.wa2 -mat whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x142299 | 1138392 | double array |
data_name | 1x6 | 12 | char array |
map | 64x3 | 1536 | double array |
sizes | 5x2 | 80 | double array |
valTHR | 0x0 | 0 | double array |
wave_name | 1x4 | 8 | char array |
Переменные coefs и sizes содержите структуру разложения вейвлета. Другие переменные содержат имя вейвлета, палитру и имя файла, содержащее данные. Переменный valTHR пусто, поскольку синтезируемое изображение совпадает с исходным.
Сохраните опции, также доступны при выполнении шумоподавления или сжатия в инструменте Wavelet 2-D. В окне Wavelet 2-D Denoising можно сохранить denoised образ и разложение. То же самое сохраняется для окна Wavelet 2-D Compression. Таким образом, можно сохранить много различных испытаний из окон Denoising и Compression, не возвращаясь к основному окну Wavelet 2-D во время процесса подстройки. При сохранении синтезируемого сигнала, разложения или коэффициентов к MAT-файлу, mat расширение файла не необходимо. Можно сохранить приближения индивидуально для каждого уровня или сохранить их целиком.
Можно загрузить изображения, коэффициенты или разложения в приложение Wavelet Analyzer. Информация, которую вы загружаете, возможно, ранее экспортировалась из приложения Wavelet Analyzer, и затем управлялась в рабочей области; или это, возможно, была информация, которую вы сгенерировали первоначально из командной строки.
Или в случае, необходимо наблюдать строгие форматы файлов и структуры данных, используемые инструментом Wavelet 2-D, или иначе в ошибки закончатся, когда вы попытаетесь загрузить информацию.
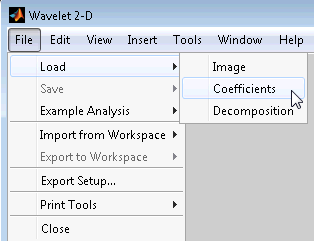
Загрузка Изображений. Этот тулбокс поддерживает только индексированные изображения. Индексируемое изображение является матрицей, содержащей только целые числа от 1 до n, где n количество, раскрашивает изображение.
Это изображение может опционально сопровождаться n- 3 матрицы под названием map. Это - палитра, сопоставленная с изображением. Когда MATLAB отображает такое изображение, он использует значения матрицы, чтобы искать требуемый цвет в этой палитре. Если палитра не дана, инструмент Wavelet 2-D использует монотонную палитру с max(max(X))min(min(X))+1 цвета.
Чтобы загрузить изображение, вы создали в своем рабочем пространстве MATLAB в инструмент Wavelet 2-D, сохраните образ (и опционально, переменная map) в MAT-файле (с дополнительным mat или другой).
Например, предположите, что вы создали названный мозг изображения и хотите анализировать его в инструменте Wavelet 2-D. Ввод
X = brain; map = pink(256); save myfile X map
Чтобы загрузить это изображение в инструмент Wavelet 2-D, используйте пункт меню File> Load> Image.
Диалоговое окно появляется, который позволяет вам выбрать соответствующий MAT-файл, чтобы загрузиться.
Графические инструменты позволяют вам загружать изображение, которое не содержит целые числа от 1 до n. Расчеты правильны, потому что они действуют непосредственно на матрицу, но отображение изображения является странным. Значения меньше чем 1 оценен как 1, значения, больше, чем n, оценены как n и действительное значение в интервале [1, n] оценен как самое близкое целое число.
Коэффициенты, приближения и детали, произведенные разложением вейвлета, не индексируются матрицы изображений.
Чтобы отобразить эти изображения подходящим способом, инструмент Wavelet 2-D следует этим правилам:
Восстановленные приближения отображены с помощью палитры map.
Коэффициенты и восстановленные детали отображены с помощью палитры map примененный перемасштабированная версия матриц.
С первой 2D переменной сталкиваются в файле (кроме переменной map, то, которое резервируется для палитры), рассматривается изображением. Переменные смотрятся в алфавитном порядке.
Загрузка Дискретных Коэффициентов Преобразования Вейвлета. Чтобы загрузить коэффициенты дискретного вейвлета преобразовывает (DWT) в инструмент Wavelet 2-D, сначала сохраните соответствующие данные в MAT-файле, который должен содержать, по крайней мере, эти две переменные:
coefs, содействующий вектор
sizes, бухгалтерская матрица
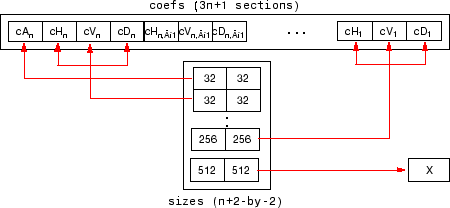
Для индексируемого изображения матричный sizes n+2- 2 массива:
Для изображения истинного цвета, матричного sizes n+2- 3:
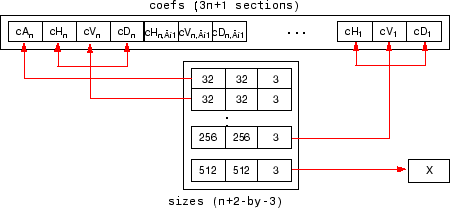
Переменный coefs должен быть вектор конкатенированных коэффициентов DWT. coefs вектор для n- разложение уровня содержит 3n+1 разделы, состоя из уровня-n коэффициенты приближения, сопровождаемые горизонталью, вертикальными, и диагональными коэффициентами детали, в том порядке, для каждого уровня. Переменный sizes матрица, строки которой задают размер cAn, размер cHn (или cVn, или cDn)..., размер cH1 (или cV1, или cD1), и размер оригинального изображения X. Размеры вертикальных и диагональных деталей совпадают с горизонтальной деталью.
После построения или редактирования соответствующих данных в вашей рабочей области, ввести
save myfile coefs sizes
Используйте пункт меню File> Load> Coefficients от инструмента Wavelet 2-D, чтобы загрузить данные в графический инструмент.
Диалоговое окно появляется, позволяя вам выбрать папку и файл, в котором находятся ваши данные.
Загрузка Разложений. Чтобы загрузить дискретный вейвлет преобразовывают данные о разложении в инструмент Wavelet 2-D, необходимо сначала сохранить соответствующие данные в MAT-файле (с дополнительным wa2 или другой).
MAT-файл содержит эти переменные.
| Переменная | Состояние | Описание |
|---|---|---|
coefs | Необходимый | Вектор конкатенированных коэффициентов DWT |
sizes | Необходимый | Матричные размеры определения компонентов |
wave_name | Необходимый | Имя определения вектора символов вейвлета используется в разложении (например, |
map | Дополнительный |
|
data_name | Дополнительный | Имя определения вектора символов разложения |
После построения или редактирования соответствующих данных в вашей рабочей области, ввести
save myfile.wa2 coefs sizes wave_name
Используйте пункт меню File> Load> Decomposition от инструмента Wavelet 2-D, чтобы загрузить данные о разложении изображений.
Диалоговое окно появляется, позволяя вам выбрать папку и файл, в котором находятся ваши данные.
При загрузке изображения, разложения или коэффициентов из MAT-файла, расширение этого файла свободно. mat расширение не необходимо.