Взаимная связь

Взаимная связь является электромагнитным взаимодействием между антенными элементами в массиве. Ток, разработанный в каждом антенном элементе массива, зависит от их собственного возбуждения и также от вкладов от смежных антенных элементов. Взаимная связь обратно пропорциональна интервалу между различными антенными элементами в массиве. Взаимная связь в массиве вызывает:

Изменения в диаграмме направленности массива
Изменения во входном импедансе отдельных антенных элементов в массиве

Чтобы охарактеризовать взаимную связь, можно использовать взаимный импеданс, S-параметры, связывающуюся матрицу или встроенный шаблон элемента.

Активный или импеданс скана

Активный импеданс или импеданс скана, является входным импедансом каждого антенного элемента в массиве, когда все элементы взволнованы.

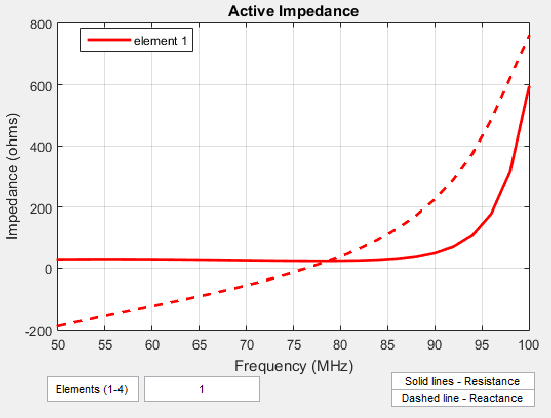
Активный импеданс массива зависит от:

Конфигурация массивов
Интервал между элементами
Сдвиг фазы применяется в каждом элементе

Взаимный импеданс

Эффект взаимной связи наблюдается или моделируется путем варьирования пробела между антенными элементами в массиве. Любое изменение в межэлементных интервалах изменяет взаимный импеданс между антенными элементами. Например, график показывает взаимный импеданс двухэлементного дипольного массива как функция межэлементного интервала.

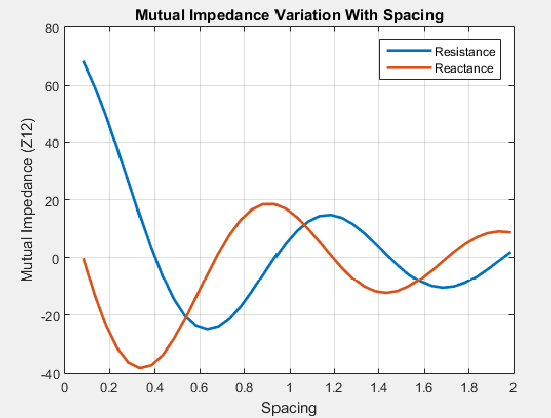
График показывает это интервалом между увеличениями элементов, взаимным импедансом, и следовательно взаимными уменьшениями связи.

Связь матрицы

Связывающаяся матрица используется, чтобы охарактеризовать взаимную связь между антенными элементами на уровне порта. Эта матрица вычисляется с помощью S-параметров или Z-параметров и используется, чтобы разъединить массив.

Матрица S-параметра

Чтобы вычислить связывающуюся матрицу, можно использовать матрицу S-параметра. Вы вычисляете каждый столбец матрицы S-параметра путем питания антенны в том столбце 1V. Считайте массив элемента расположенным в 2x2 сетка. Визуализируйте сетку и числа элемента с помощью layout.

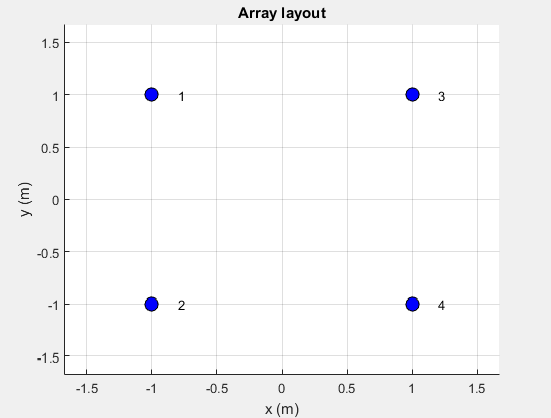
В этом массиве существует четыре порта. Соответствующая матрица S-параметра имела бы размер 4 x 4:

$S = (\begin{matrix} s_{11} & s_{12} & s_{13} & s_{14} \\ s_{21} & s_{22} & s_{23} & s_{24} \\ s_{31} & s_{32} & s_{33} & s_{34} \\ s_{41} & s_{42} & s_{43} & s_{44} \end{matrix})$

Во время этого измерения отключите отдых антенных элементов с помощью ссылочного сопротивления 50 Ом. Сопротивление завершения внутренне установлено в значение по умолчанию 50 Ом и может быть не использовано во время вычисления. Если завершение отличается, задайте значение сопротивления при использовании этой функции. Диагональные термины в показанной матрице, представляйте самовзаимодействие, которое также обычно упоминается как отражательный коэффициент. Недиагональные условия получают взаимную связь между портами антенны.

Использование sparameters вычислить матрицу связи S-параметра массива в Antenna Toolbox™.

Фактор массивов и умножение шаблона

Основанием теории массивов является теорема умножения шаблона. Эта теорема утверждает, что объединенный шаблон идентичных элементов массива N описывается как времена шаблона элемента фактор массивов.

Фактор массивов вычисляется с помощью формулы:

$A F = \sum_{i = 0}^{N} V (i) \cdot e^{(k \sin θ \cos φ \cdot x (i) + k \sin φ \cdot y (i) + k \cos θ \cdot z (i))}$

где:

N является числом элементов в массиве.
V является приложенным напряжением (амплитуда и фаза) в каждом элементе в массиве.
k является номером волны.
тета и phi являются углами азимута и вертикальным изменением.
x, y, и z являются Декартовы координаты местоположений канала для каждого антенного элемента массива.

Если фактор массивов вычисляется с помощью вышеупомянутого уравнения, можно вычислить диаграмму направленности массива как продукт фактора массивов и диаграмма направленности отдельного антенного элемента массива.

Шаблон массивов = AF* отдельный шаблон антенного элемента

Анализ принимает, что элементы массива разъединяются. Это означает, что ток в одном элементе не волнует токи в других элементах или нет никакой взаимной связи между различными элементами массива. Это - самое серьезное ограничение теоремы умножения шаблона, ограничивая ее использование массивами с большим интервалом элемента.

Например:

Вычислите шаблон массивов прямоугольного массива диполей в x-y плоскости с интервалом полуlambda

fc = 1e9;
lambda = physconst('lightspeed')/fc;
az = -180:0.1:180;
el = -90:0.1:90;

%% Element
d = design(dipole,1e9);
d.Tilt = 90;
d.TiltAxis = [0 1 0];
 
%% Array
r = rectangularArray;
r.Element       = d;
r.RowSpacing    = lambda/2;
r.ColumnSpacing = lambda/2;
figure; show(r) ;
figure; patternMultiply(r, fc, az, el);

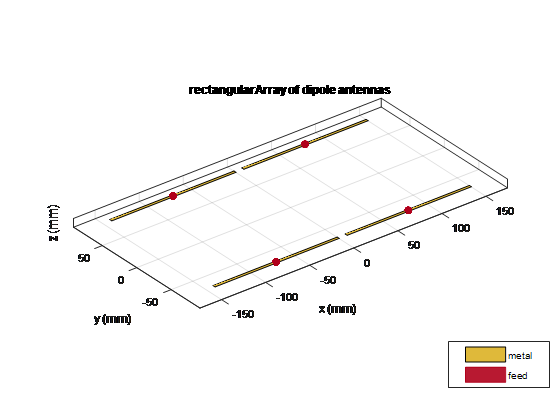
Увеличьте размер прямоугольного массива к 200k элементам. Ниже время, потраченное для расчета и расчетной направленности.

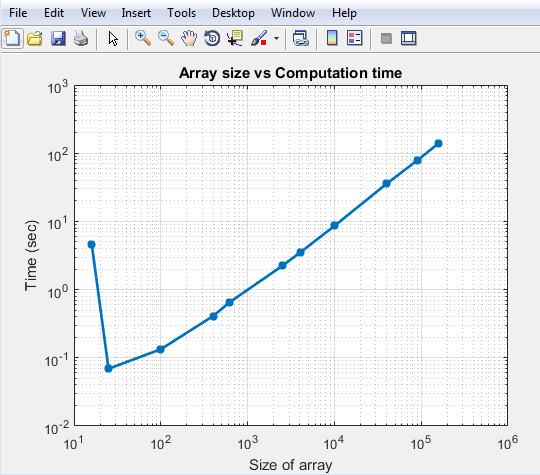
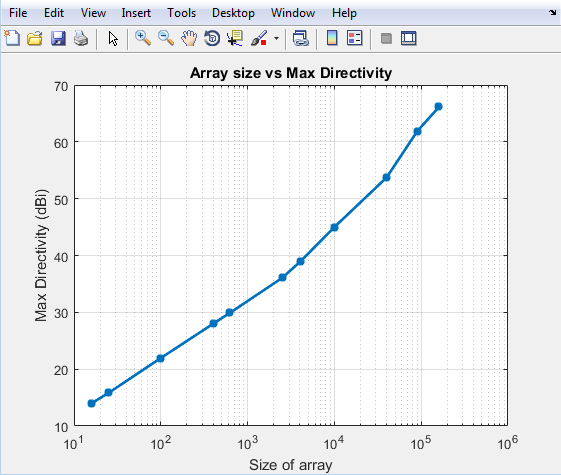
Вы видите, что время, потраченное, чтобы решить 100k массив, меньше 100 секунд. Начальный удар как раз к небольшому массиву - то, потому что вы выполняете анализ EM, чтобы вычислить шаблон отдельного дипольного элемента в массиве. Если этот анализ сделан, результаты кэшируются, и последовательные вызовы не выполняют анализа EM. В результате увеличение вовремя довольно линейно. Это - самое большое преимущество использования умножения шаблона. Это позволяет вам решить большие массивы быстро и с требованиями ограниченной памяти.

Изолированный шаблон элемента

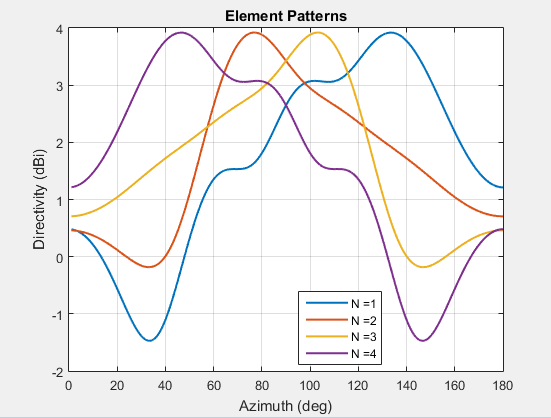
Шаблоны отдельных элементов в небольших массивах значительно варьируются. Поэтому вы не можете использовать умножение шаблона для полного шаблона массивов, потому что изолированный шаблон элемента принимает, что все элементы имеют тот же шаблон.

Можно вычислить полный шаблон массивов небольших массивов путем графического вывода шаблона все элементы отдельно в небольшом массиве. Чтобы получить этот шаблон, каждый элемент индивидуально взволнован и остальная часть элементов массива, отключенных с помощью ссылочного импеданса. График показывает диаграмму направленности отдельных элементов 4 - массив элемента.

Встроенный шаблон элемента

Встроенный шаблон элемента является шаблоном одного элемента, встроенного в конечный массив, вычисленный путем управления определенным (обычно центральное) элемент в массиве. Остальная часть элементов массива отключена с помощью ссылочного импеданса. Этот метод полезен для большого массива, потому что эффект взаимной связи на отдельном элементе получен. Важно отметить, что краевые эффекты могут быть проигнорированы, поскольку размер массива принят, чтобы быть очень большим. Распространено использовать центральный антенный элемент для этого вычисления. Должный, к размеру массива диаграммы направленности элементов в массиве могут быть аппроксимированы встроенным шаблоном элемента вместо изолированного шаблона элемента. Наконец, умножение шаблона используется, чтобы вычислить полный шаблон массивов.

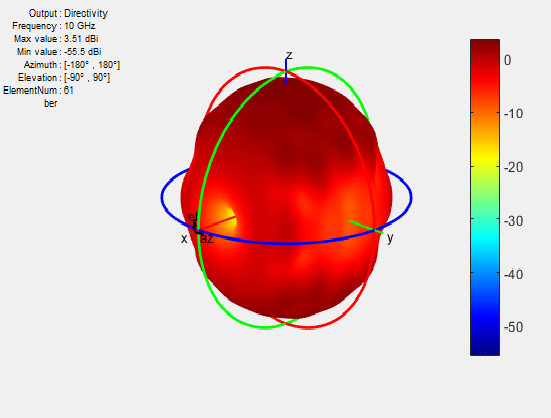
Рисунок показывает встроенный шаблон элемента центрального элемента в 11x11 массив. Можно также вычислить встроенный шаблон элемента как величину электрического поля.

Изолированный шаблон элемента не рекомендуется для больших массивов, когда этот метод не составляет связывающиеся эффекты элементов вокруг этого.

Отсканируйте слепоту

В больших массивах возможно, что направленность массивов уменьшает решительно в определенных углах сканирования. В этих углах сканирования, называемых мертвыми углами, массив не излучает питание, подавшее на ее входных терминалах [3]. Слепота скана может появиться при использовании этих общих механизмов:

Поверхностное возбуждение волны
Скрипучее возбуждение лепестка

Чтобы обнаружить слепоту скана в больших конечных массивах, изучите встроенный шаблон элемента. В бесконечном анализе массивов этот шаблон известен как шаблон элемента массива.

Ссылки

[1] Стуцмен, В.Ль. Тиле, Теория Г.А. Антенны и Проект, 3-й Выпуск. Нью-Йорк: Вайли, 2013, p. 307.

Документация