Эта модель, doc_gray_code, показывает линию связи с помощью серо-закодированной модуляции 8-PSK. Серое кодирование является методом, часто используемым в многоуровневых схемах модуляции минимизировать частоту ошибок по битам путем упорядоченного расположения символов модуляции так, чтобы бинарные представления смежных символов отличались только на один бит.
Модель в качестве примера включает эти блоки:
Блок Random Integer Generator служит источником, производя последовательность целых чисел.
Блок Integer to Bit Converter преобразует каждое целое число в соответствующее бинарное представление.
Блок AWGN Channel добавляет белый Гауссов шум в модулируемые данные.
Блок M-PSK Demodulator Baseband демодулирует поврежденные данные.
Блок Bit to Integer Converter преобразует каждое бинарное представление соответствующему целому числу.
Одна копия блока Error Rate Calculation (пометил Error Rate Calculation1 в этой модели), сравнивает демодулируемые целочисленные данные с данными о первоисточнике, давая к ошибочной статистике символа. Выход блока Error Rate Calculation является трехэлементным вектором, содержащим расчетный коэффициент ошибок, количество ошибок, наблюдаемых, и обработанный объем данных.
Другая копия библиотечного блока Error Rate Calculation (пометил Error Rate Calculation2 в этой модели), сравнивает демодулируемые двоичные данные с бинарными представлениями исходных данных, давая к статистике битовой ошибки.
В этой модели, блоке M-PSK Modulator Baseband:
Принимает входные параметры с бинарным знаком, которые представляют целые числа между 0 и M − 1, где M является размером алфавита
Двоичные представления карт точкам созвездия с помощью серо-закодированного упорядоченного расположения
Производит фазовращатель комплекса модульной величины выходные параметры, с равномерно расположенными с интервалами фазами между 0 и 2π (M − 1)/M
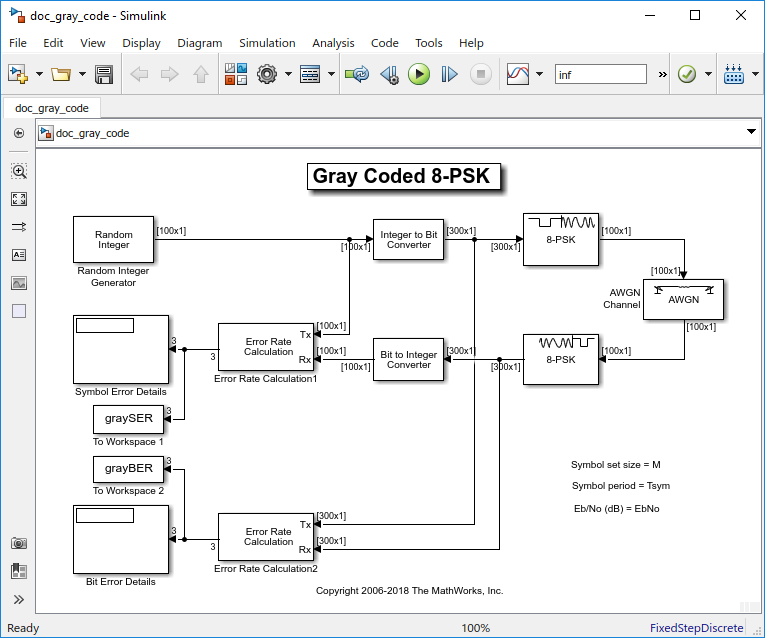
Таблица показывает, которому бинарные представления во входе соответствуют который фазовращатели в выходе. Второй столбец таблицы является промежуточным представлением, которое блок использует в его расчетах.
| Вход модулятора | Серо-закодированное упорядоченное расположение | Модулятор Выход |
|---|---|---|
000 | 0 | exp(0) = 1 |
001 | 1 | exp(jπ/4) |
010 | 3 | exp(j 3π/4) |
011 | 2 | exp(j 2π/4) = exp(jπ/2) |
100 | 7 | exp(j 7π/4) |
101 | 6 | exp(j 6π/4) = exp(j 3π/2) |
110 | 4 | exp(j 4π/4) = exp(jπ) |
111 | 5 | exp(j 5π/4) |
Таблица ниже видов первые два столбца приведенной выше таблицы, согласно выходным значениям. Эта сортировка делает его более ясным, что полный эффект этой подсистемы является отображением Кода Грея, как показано на рисунке ниже. Заметьте, что числа во втором столбце приведенной ниже таблицы появляются в против часовой стрелки порядке на рисунке.
| Модулятор Выход | Вход модулятора |
|---|---|
exp(0) | 000 |
exp(j π/4) | 001 |
exp(j 2π/4) = exp(jπ/2) | 011 |
exp(j 3π/4) | 010 |
exp(j 4π/4) = exp(jπ) | 110 |
exp(j 5π/4) | 111 |
exp(j 6π/4) = exp(j 3π/2) | 101 |
exp(j 7π/4) | 100 |
Можно анализировать данные, которые пример производит, чтобы сравнить теоретическую эффективность с эффективностью симуляции.
Теоретическая вероятность появления ошибки символа MPSK
где erfc дополнительная функция ошибок, Es/N0 является отношением энергии в символе к шумовой степени спектральная плотность, и M является количеством символов.
Чтобы определить вероятность битовой ошибки, вероятность появления ошибки символа, PE, должна быть преобразована в свою эквивалентную битовую ошибку. Нет никакой общей формулы для символа к преобразованию битовой ошибки. Верхний и нижние пределы, тем не менее, легки установить. Фактическая вероятность битовой ошибки, Pb, как могут показывать, ограничена
Нижний предел соответствует случаю, где символы подверглись Грэю, кодирующему. Верхний предел соответствует случаю чистого двоичного кодирования.
Чтобы протестировать схему модуляции Кода Грея в этой модели, симулируйте graycode модель для области значений значений Eb/N0. Если вы хотите изучить частоты ошибок по битам, но не коэффициенты ошибок символа, то можно использовать bertool графический интерфейс пользователя как описано в BERTool.
Остальная часть этого раздела изучает и бит и коэффициенты ошибок символа и следовательно не использует bertool.
Поскольку увеличение значения Eb/N0 понижает количество произведенных ошибок, продолжительность каждой симуляции должна быть увеличена, чтобы гарантировать, что статистические данные ошибок остаются устойчивыми.
Используя sim (Simulink) управляет, чтобы запустить симуляцию Simulink® из командного окна MATLAB®, следующий код генерирует данные для кривых коэффициента ошибок и частоты ошибок по битам символа. Это считает значения Eb/N0 в области значений от 0 дБ до 12 дБ, с шагом 2 дБ.
M = 8; Tsym = 0.2; BERVec = []; SERVec = []; EbNoVec = [0:2:12]; for n = 1:length(EbNoVec); EbNo = EbNoVec(n); sim('doc_gray_code') ; SERVec(n,:) = graySER; BERVec(n,:) = grayBER; end;
После симуляции для полного набора значений Eb/N0 можно построить результаты с помощью этих команд:
semilogy( EbNoVec,SERVec(:,1), 'o', EbNoVec, BERVec(:,1), '*' ); legend ( 'Symbol error rate', 'Bit error rate' ); xlabel ( 'Eb/No (dB)' ); ylabel( 'Error Probability' ); title ( 'Symbol and Bit Error Probability' );
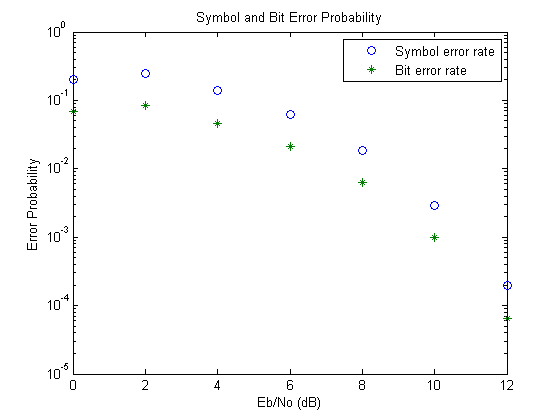
Как дальнейшее осуществление, с помощью данных, полученных из berawgn, можно построить теоретические кривые на тех же осях с результатами симуляции. Можно также сравнить Грэя, кодирующего с чистым двоичным кодированием путем изменения M-PSK Modulator Baseband и блоков M-PSK Demodulator Baseband так, чтобы их параметрами Constellation ordering был Binary вместо Gray.