Вычислите оценки фильтра для входных параметров с помощью Кальмана адаптивный алгоритм фильтра
dspobslib
Примечание
Блок Kalman Adaptive Filter все еще поддерживается, но, вероятно, будет obsoleted в будущем релизе. Мы строго рекомендуем заменить этот блок на блок Kalman Filter.
Блок Kalman Adaptive Filter вычисляет оптимальную линейную минимальную среднеквадратическую оценку (MMSE) КИХ-коэффициентов фильтра с помощью алгоритма прогноза с одним шагом. Этот алгоритм Фильтра Калмана основан на следующей физической реализации динамической системы.
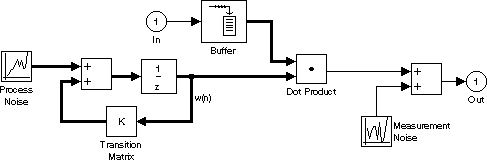
Фильтр Калмана принимает, что нет никаких детерминированных изменений в касаниях фильтра в зависимости от времени (то есть, матрица перехода является идентичностью), и что единственный заметный выход от системы является фильтром выход с аддитивным шумом. Соответствующий Фильтр Калмана описывается в матричной форме как
Переменные следующие
| Переменная | Описание |
|---|---|
n | Текущая итерация алгоритма |
u(n) | Буферизированные входные выборки на шаге n |
K(n) | Корреляционная матрица ошибки оценки состояния |
g(n) | Вектор из Кальмана получает на шаге n |
Вектор из касания фильтра оценивает на шаге n | |
y(n) | Отфильтрованный выход на шаге n |
e(n) | Ошибка расчета на шаге n |
d(n) | Желаемый ответ на шаге n |
QM | Корреляционная матрица шума измерения |
QP | Корреляционная матрица шума процесса |
Корреляционные матрицы, QM и QP, заданы в диалоговом окне параметра скалярными условиями отклонения, которые будут помещены по матричным диагоналям, таким образом гарантируя, что эти матрицы симметричны. Алгоритм фильтра на основе этого ограничения также известен как Фильтр Калмана случайного обхода.
Реализация алгоритма в блоке оптимизирована путем использования симметрии входной ковариационной матрицы K(n) . Это сокращает общее число расчетов на коэффициент два.
Значок блока имеет метки порта, соответствующие вводам и выводам алгоритма Кальмана. Обратите внимание на то, что входные параметры к портам In и Err должны быть основанными на выборке скалярами с той же сложностью. Сигнал в порте Out является скаляром, в то время как сигнал в порте Taps является основанным на выборке вектором.
| Блокируйте порты | Соответствующие переменные |
|---|---|
| \in | u, скалярный вход, который внутренне буферизуется в векторный u(n) |
y(n), отфильтрованный скалярный выход | |
| Допустить ошибку | e(n), скалярная ошибка расчета |
| Касания | , вектор из оценок касания фильтра |
Дополнительное Адаптируется, входной порт добавляется, когда вы устанавливаете флажок Adapt port в диалоговом окне. Когда этот порт включен, блочно-непрерывно адаптирует коэффициенты фильтра, в то время как вход Adapt является ненулевым. Вход с нулевым знаком к Adapt порт заставляет блок прекращать адаптироваться и содержать коэффициенты фильтра в их текущих значениях до следующего ненулевого входа Adapt.
Параметр FIR filter length задает длину фильтра, который оценивает алгоритм Кальмана. Measurement noise variance и параметры Process noise variance задают корреляционные матрицы шума измерения и процесса, соответственно. Measurement noise variance должен быть скаляром, в то время как Process noise variance может быть вектором из значений, которые будут помещены по диагонали или скаляру, который будет повторен для диагональных элементов.
Initial value of filter taps задает начальное значение как вектор, или как скаляр, который будет повторен для всех векторных элементов. Initial error correlation matrix задает начальное значение K(0) и может быть диагональной матрицей, вектором из значений, которые будут помещены по диагонали или скаляру, который будет повторен для диагональных элементов.
Длина КИХ-фильтра.
Значение, чтобы появиться по диагонали корреляционной матрицы шума измерения. Настраиваемый (Simulink).
Значение, чтобы появиться по диагонали корреляционной матрицы шума процесса. Настраиваемый (Simulink).
Начальный КИХ фильтрует коэффициенты.
Начальное значение ошибочной корреляционной матрицы.
Включает Adapt порт.
Haykin, S. Адаптивная Теория Фильтра. 3-й редактор Englewood Cliffs, NJ: Prentice Hall, 1996.
Плавающая точка двойной точности
Плавающая точка с одинарной точностью
| LMS адаптивный (устаревший) фильтр | DSP System Toolbox |
| RLS адаптивный (устаревший) фильтр | DSP System Toolbox |
Смотрите Подавление помех в Simulink Используя Нормированный Адаптивный Фильтр LMS для сопутствующей информации.