В цифровом оборудовании числа хранятся в двоичных словах. Двоичное слово является последовательностью фиксированной длины битов (1's и 0). Путем аппаратные компоненты или функции программного обеспечения интерпретируют эту последовательность 1's, и 0 задан по условию тип.
Двоичные числа представлены или как с плавающей точкой или как типы данных с фиксированной точкой. В этом разделе мы обсуждаем много условий и концепций, относящихся к числам фиксированной точки, типам данных и математике.
Тип данных с фиксированной точкой характеризуется размером слова в битах, положении двоичной точки и со знаком из номера, который может быть подписан или без знака. Числа со знаком и типы данных могут представлять и положительные и отрицательные величины, тогда как числа без знака и типы данных могут только представлять значения, которые больше или равны нулю.
Положение двоичной точки является средними значениями, которыми значения фиксированной точки масштабируются и интерпретируются.
Например, бинарное представление обобщенного номера фиксированной точки (или подписанный или без знака) показывают ниже:
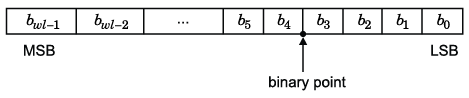
где
bi является ith двоичной цифрой.
wl является количеством битов в двоичном слове, также известном как размер слова.
b wl –1 является местоположением старшего значащего, или самый высокий, бит (MSB). В двоичных числах со знаком этот бит является знаковым битом, который указывает, положителен ли номер или отрицателен.
b0 является местоположением младшего значащего, или самый низкий, бит (LSB). Этот бит в двоичном слове может представлять наименьшее значение. Весом LSB дают:
где, fractionlength является количеством битов справа от двоичной точки.
Биты слева от двоичной точки являются целочисленными битами и/или знаковыми битами, и биты справа от двоичной точки являются дробными битами. Количество битов слева от двоичной точки известно как целочисленную длину. Двоичной точке в этом примере показывают четыре места слева от LSB. Поэтому номер, как говорят, имеет четыре дробных бита или дробную длину четыре.
Типы данных с фиксированной точкой могут быть или подписаны или без знака.
Бинарные числа фиксированной точки со знаком обычно представляются одним из трех способов:
Знак/величина – Представление фиксированной точки со знаком или чисел с плавающей запятой. В представлении знака/величины один бит двоичного слова является всегда специализированным знаковым битом, в то время как остающиеся биты слова кодируют величину номера. Отрицание с помощью представления знака/величины состоит из зеркального отражения знакового бита от 0 (положительный) 1 (отрицанию), или от 1 до 0.
Поразрядное дополнение до единицы
Дополнение Туо – дополнение Туо является наиболее распространенным представлением чисел фиксированной точки со знаком. Смотрите Дополнение Туо для получения дополнительной информации.
Числа фиксированной точки без знака могут только представлять числа, больше, чем или равный нулю.
В [Наклонное Смещение] представление, числа фиксированной точки могут быть закодированы согласно схеме
где наклон может быть описан как
Корректировка наклона термина иногда используется в качестве синонима для дробного наклона.
В тривиальном случае клонитесь = 1 и смещение = 0. Масштабирование всегда тривиально для чистых целых чисел, таково как int8, и также для истинных типов с плавающей точкой, одного и двойных.
Целое число иногда называется сохраненным целым числом. Это - необработанное двоичное число, в котором двоичная точка приняла, чтобы быть в ультраправом из слова. В Системных Тулбоксах отрицание экспоненты часто упоминается как дробная длина.
Наклон и смещение вместе представляют масштабирование номера фиксированной точки. В номере с нулевым смещением только наклон влияет на масштабирование. Номер фиксированной точки, который только масштабируется положением двоичной точки, эквивалентен номеру в Fixed-Point Designer™ [Наклонное Смещение] представление, которое имеет равное нулю смещение и наклонная корректировка, равная одной. Это упоминается как бинарное масштабирование только для точки или масштабирование степени двойки:
или
В программном обеспечении System Toolbox можно задать тип данных с фиксированной точкой и масштабирующийся для выхода или параметров многих блоков путем определения размера слова и фракционировать продолжительность количества. Размер слова и дробная длина задают весь тип данных, и масштабирующаяся информация для двоичной точки только сигнализирует.
Все Системные блоки Тулбокса, которые поддерживают сигналы поддержки типов данных с фиксированной точкой с двоичной точкой, только масштабирующейся. Много блоков фиксированной точки, которые не выполняют арифметические операции, но просто перестраивают данные, такие как Задержка и Матрица, Транспонируют, также поддерживают сигналы с [Наклонное Смещение] масштабирование.
Необходимо обратить внимание на точность и область значений типов данных с фиксированной точкой и масштабирований, которые вы выбираете для блоков в ваших симуляциях, для того, чтобы знать, будет ли округление методов вызвано или если переполнение произойдет.
Область значений является промежутком чисел, которые могут представлять тип данных с фиксированной точкой и масштабирование. Область значений представимых чисел для дополнительного количества фиксированной точки two размера слова wl, масштабируя S и смещение B проиллюстрирована ниже:

И для подписанных и для количеств фиксированной точки без знака любого типа данных, количество различных комбинаций двоичных разрядов 2wl.
Например, в дополнении two, отрицательные числа должны быть представлены, а также нуль, таким образом, максимальное значение является 2wl–1. Поскольку существует только одно представление для нуля, существует неравное количество положительных и отрицательных чисел. Это означает, что существует представление для-2wl–1, но не для 2wl–1:
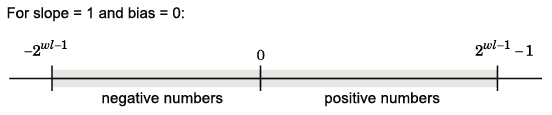
Полный спектр является самой широкой областью значений для типа данных. Для типов с плавающей точкой полный спектр – ∞ к ∞. Для целочисленных типов полный спектр является диапазоном от самого маленького до самого большого целочисленного значения (конечного), тип может представлять. Например, от-128 до 127 для 8-битного целого числа со знаком.
Обработка переполнения. Поскольку тип данных с фиксированной точкой представляет числа в конечной области значений, переполнение может произойти, если результат операции больше или меньше, чем числа в той области значений.
Программное обеспечение System Toolbox не позволяет вам добавлять "сторожевые" разряды в тип данных на лету во избежание переполнения. "Сторожевые" разряды являются дополнительными битами или в аппаратном регистре или в программном моделировании, которые добавляются к верхнему уровню двоичного слова, чтобы гарантировать, что никакая информация не потеряна в случае переполнения. Любые "сторожевые" разряды должны быть выделены после инициализации модели. Однако программное обеспечение действительно позволяет вам или насыщать или переносить переполнение. Насыщение представляет положительное переполнение как самое большое положительное число в области значений, используемой и отрицательное переполнение как самое большое отрицательное число в используемой области значений. Перенос использования арифметика по модулю, чтобы бросить переполнение назад в представимую область значений типа данных. Смотрите Арифметику По модулю для получения дополнительной информации.
Точность номера фиксированной точки является различием между последовательными значениями, представимыми его типом данных и масштабированием, которое равно значению его младшего значащего бита. Значение младшего значащего бита, и поэтому точность номера, определяются количеством дробных битов. Значение фиксированной точки может быть представлено в половине точности его типа данных и масштабирования. Термин разрешение иногда используется как синоним для этого определения.
Например, представление фиксированной точки с четырьмя битами справа от двоичной точки имеет точность 2-4 или 0.0625, который является значением ее младшего значащего бита. Любой номер в области значений этого типа данных и масштабирования может быть представлен в (2-4)/2 или 0.03125, который является половиной точности. Это - пример представления номера с конечной точностью.
Округление Режимов. Когда вы представляете числа конечной точностью, не, каждый номер в доступной области значений может быть представлен точно. Если номер не может быть представлен точно заданным типом данных и масштабированием, это округлено к представимому номеру. Несмотря на то, что точность всегда теряется в округляющейся операции, стоимость операции и объем смещения, которое введено, зависят от самого округляющегося режима. Чтобы предоставить вам большую гибкость в компромиссе между стоимостью и смещением, программное обеспечение DSP System Toolbox™ в настоящее время поддерживает следующие режимы округления:
Ceiling округляет результат вычисления к самому близкому представимому номеру в направлении положительной бесконечности.
Convergent округляет результат вычисления к самому близкому представимому номеру. В случае ничьей, Convergent раунды к самому близкому четному числу. Это - наименее смещенный режим округления, обеспеченный тулбоксом.
Floor, то, которое эквивалентно усечению, округляет результат вычисления к самому близкому представимому номеру в направлении отрицательной бесконечности. Операция усечения приводит к отбрасыванию одного или нескольких младших значащих битов от номера.
Nearest округляет результат вычисления к самому близкому представимому номеру. В случае ничьей, Nearest раунды к самому близкому представимому номеру в направлении положительной бесконечности.
Round округляет результат вычисления к самому близкому представимому номеру. В случае ничьей, Round положительные числа раундов к самому близкому представимому номеру в направлении положительной бесконечности и отрицательные числа раундов к самому близкому представимому номеру в направлении отрицательной бесконечности.
Simplest округляет результат вычисления с помощью округляющегося режима (Floor или Zero) это добавляет наименьшее количество суммы дополнительного кода округления к вашему сгенерированному коду. Для получения дополнительной информации смотрите Округление Режима: Самый Простой (Fixed-Point Designer).
Zero округляет результат вычисления к самому близкому представимому номеру в направлении нуля.
Чтобы узнать больше о каждом из этих режимов округления, смотрите Округление (Fixed-Point Designer).
Для прямого сравнения округляющихся режимов смотрите Выбор Rounding Method (Fixed-Point Designer).