Точность ограничивается наклоном. Чтобы достигнуть максимальной точности, необходимо сделать наклон как можно меньше при хранении области значений соответственно большой. Смещение настроено при взаимодействии с наклоном.
Примите, что максимальные и минимальные реальные значения даны макс. (V) и min (V), соответственно. Эти пределы могут быть известны на основе физических принципов или технических факторов. Чтобы максимизировать точность, необходимо выбрать округляющуюся схему и насыщает ли переполнение или переносится. Для упрощения этот пример принимает, что минимальное реальное значение соответствует минимальному закодированному значению, и максимальное реальное значение соответствует максимальному закодированному значению. Используя схему кодирования, описанную в Масштабировании, этими значениями дают
Решая для наклона, вы добираетесь
Эта формула независима от округления и проблем переполнения, и зависит только от размера слова, ws.
Дополнение конечными нулями включает расширение младшего значащего бита (LSB) номера с дополнительными битами. Этот метод включает движение от низкой точности до более высокой точности.
Например, предположите, что два числа вычтены друг от друга. Во-первых, экспоненты должны быть выровнены, который обычно включает сдвиг вправо номера с меньшим значением. В выполнении этого сдвига значительные цифры могут “уменьшиться” направо. Однако, когда соответствующее количество дополнительных битов добавлено, точность результата максимизируется. Рассмотрите два 8-битных числа фиксированной точки, которые близки в значении и вычтенные друг от друга:
где q является целым числом. Чтобы выполнить эту операцию, экспоненты должны быть равными:
Если главный номер дополнен двумя нулями, и нижний номер дополнен одним нулем, то вышеупомянутое уравнение становится
который приводит к более точному результату. Пример дополнения конечными нулями в модели Simulink® проиллюстрирован в Цифровом диспетчере Рилизэйшне.
Следующие блоки Simulink фиксированной точки обеспечивают режим для масштабных коэффициентов, значения которых являются постоянными векторами или матрицами:
Этот режим масштабирования основан на единственном двоичной точкой масштабировании. Используя этот режим, можно масштабировать постоянный вектор или матрицировать таким образом, что общая двоичная точка найдена на основе лучшей точности для самого большого значения в векторе или матрице.
Постоянное масштабирование для лучшей точности доступно только для типов данных с фиксированной точкой с незаданным масштабированием. Все другие типы данных с фиксированной точкой используют свое заданное масштабирование. Можно использовать Data Type Assistant (см., Задают Типы данных Используя Ассистент Типа данных) на диалоговом окне блока, чтобы включить лучший режим масштабирования точности.
На диалоговом окне блока нажмите кнопку Show data type assistant![]() .
.
Data Type Assistant появляется.
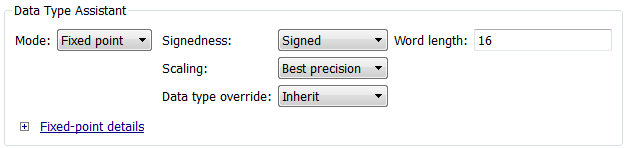
В Data Type Assistant, и из списка Mode, выбирают Fixed point.
Data Type Assistant отображает дополнительные опции, сопоставленные с типами данных с фиксированной точкой.
Из списка Scaling выберите Best precision.
Чтобы изучить, как вы можете использовать этот режим масштабирования, полагайте, что 3х3 матрица удваивается, M, заданный как
3.3333e-003 3.3333e-004 3.3333e-005 3.3333e-002 3.3333e-003 3.3333e-004 3.3333e-001 3.3333e-002 3.3333e-003
Теперь предположите, что вы задаете M как значение параметра Gain для блока Gain. Результаты определения вашего собственного масштабирования по сравнению с использованием постоянного режима масштабирования описаны здесь:
Specified Scaling
Предположим, что элементы матрицы преобразованы в 10-битный обобщенный тип данных с фиксированной точкой со знаком с единственным двоичной точкой масштабированием 2- 7 (то есть, двоичная точка расположена семь мест слева от права большая часть бита). С этим форматом данных M становится
0 0 0 3.1250e-002 0 0 3.3594e-001 3.1250e-002 0
Обратите внимание на то, что многие элементы матрицы являются нулем, и для ненулевых записей, масштабированные значения отличаются от исходных значений. Это вызвано тем, что двойное преобразовано в двоичное слово фиксированного размера и ограниченной точности для каждого элемента. Чем больше и более точный тип данных преобразования, тем более тесно масштабированные значения совпадают с исходными значениями.
Constant Scaling for Best Precision
Если M масштабируется на основе его самого большого матричного значения, вы получаете
2.9297e-003 0 0 3.3203e-002 2.9297e-003 0 3.3301e-001 3.3203e-002 2.9297e-003
Лучшая точность автоматически выбрала бы дробную длину, которая минимизирует ошибку квантования. Даже при том, что точность максимизировалась для данного размера слова, ошибки квантования могут все еще произойти. В этом примере несколько элементов все еще квантуют, чтобы обнулить.