Сложение является наиболее распространенной арифметической операцией, которую выполняет процессор. Когда два n-bit числа добавляются вместе, всегда возможно привести к результату с n + 1 ненулевая цифра из-за переноса от крайней левой цифры.
Предположим, что вы хотите суммировать три числа. Каждое из этих чисел представлено 8-битным словом, и у каждого есть различное единственное двоичной точкой масштабирование. Кроме того, выход ограничивается 8-битным словом с единственным двоичной точкой масштабированием 2-3.
Суммирование показывают в следующей модели для входных значений 19.875, 5.4375, и 4.84375.
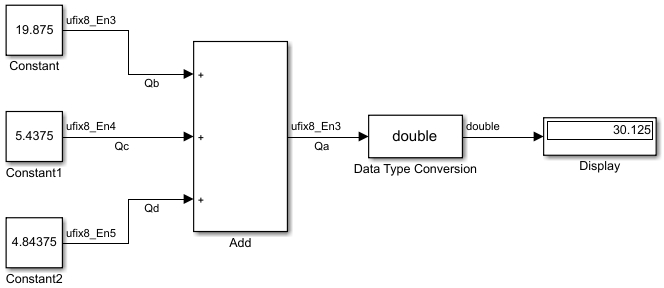
Сумма выполняет эти шаги:
Поскольку смещения являются соответствующими, начальное значение Qa тривиально:
Первый номер, который будет суммирован (19.875), имеет дробный наклон, который совпадает с выходом дробный наклон. Кроме того, двоичные точки и типы хранения идентичны, таким образом, преобразование тривиально:
Операция суммирования выполняется:
Второй номер, который будет суммирован (5.4375), имеет дробный наклон, который совпадает с выходом дробный наклон, таким образом, наклонная корректировка не нужна. Типы данных устройства хранения данных также соответствуют, но различие в двоичных точках требует, чтобы и биты и двоичная точка были смещены одно место направо:
Обратите внимание на то, что потеря в точности одного бита происходит с получившимся значением QTemp, определенного округляющимся режимом. В данном примере раунд на пол используется. Переполнение не может произойти в этом случае, потому что биты и двоичная точка оба переключены направо.
Операция суммирования выполняется:
Обратите внимание на то, что переполнение не произошло, но это возможно для этой операции.
Третий номер, который будет суммирован (4.84375), имеет дробный наклон, который совпадает с выходом дробный наклон, таким образом, наклонная корректировка не нужна. Типы данных устройства хранения данных также соответствуют, но различие в двоичных точках требует, чтобы и биты и двоичная точка были переключены два места направо:
Обратите внимание на то, что потеря в точности двухбитовых происходит с получившимся значением QTemp, определенного округляющимся режимом. В данном примере раунд на пол используется. Переполнение не может произойти в этом случае, потому что биты и двоичная точка оба переключены направо.
Операция суммирования выполняется:
Обратите внимание на то, что переполнение не произошло, но это возможно для этой операции.
Как показано здесь, результат шага 7 отличается от идеальной суммы:
Блоки, которые выполняют сложение и вычитание, включают Sum, Gain и блоки Discrete FIR Filter.