Отсеките многоугольник к мировым пределам
[latf,lonf] = flatearthpoly(lat,lon)
[latf,lonf] = flatearthpoly(lat,lon,longitudeOrigin)
[latf,lonf] = flatearthpoly(lat,lon) обрезки NaN- разделенные многоугольники заданы векторами широты и долготы lat и lon к пределам [-180 180] в долготе и [-90 90] в широте, вставляя прямые сегменты вперед +/-меридианы на 180 градусов и в полюсах. Вводы и выводы в градусах.
[latf,lonf] = flatearthpoly(lat,lon,longitudeOrigin) сосредотачивает пределы долготы на долготе, заданной скалярной долготой longitudeOrigin.
Векторные данные для географических объектов, которые охватывают полюс, неизбежно столкнутся или пересекут линию перемены даты. В то время как тулбокс правильно отображает такие многоугольники, они могут вызвать проблемы для функций как пересечение многоугольника и Логические операции, которые работают с Декартовыми координатами. Когда эти многоугольники обработаны как Декартовы координаты, результаты пересечения линии перемены даты в побочном линейном сегменте и многоугольник, отображенный, когда закрашенной фигуре не заполнили внутреннюю часть правильно.
antarctica = shaperead('landareas', 'UseGeoCoords', true,...
'Selector', {@(name) strcmp(name,'Antarctica'), 'Name'});
figure; plot(antarctica.Lon, antarctica.Lat); ylim([-100 -60])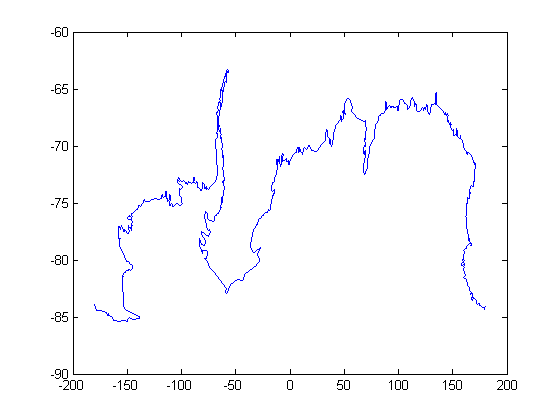
Многоугольники могут быть переформатированы более соответственно для Декартовых координат с помощью flatearthpoly функция. Результат напоминает отображение карты на цилиндрической проекции. Многоугольник соответствует линии перемены даты, раскрывается к полюсу, развертывается через долготы в полюсе и следует за линией перемены даты до другой стороны пересечения линии перемены даты.
[latf, lonf] = flatearthpoly(antarctica.Lat', antarctica.Lon'); figure; mapshow(lonf, latf, 'DisplayType', 'polygon') ylim([-100 -60]) xlim([-200 200]) axis square
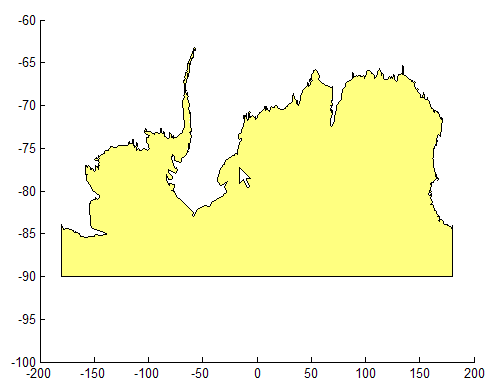
Многоугольник задан lat и lon должно быть правильно построено:
Контуры не должны пересекаться.
Вершины внешних границ должны быть в по часовой стрелке, порядок и вершины внутренних границ должны быть в против часовой стрелки порядок, такой, что внутренняя часть многоугольника всегда справа от контура.
Для получения дополнительной информации смотрите, Создают и Многоугольники Отображения.