Географические объекты, представленные векторными данными, могут или не могут быть отформатированы как многоугольники. Вообразите две переменные, latcoast и loncoast, это соответствует последовательности точек что карикатура побережье острова Великобритании. Если эти данные возвращаются к своему начальному вопросу, то многоугольник, описывающий Великобританию, существует. Эти данные могут быть отображены на графике как закрашенная фигура или как линия, и они могут логически использоваться в вычислениях как также.
Теперь предположите, что вы хотите представлять англо-шотландскую границу, происхождение западного побережья в Солуэй-Ферте в восточное побережье в Берике на твид. Эти данные могут только быть правильно заданы как линия, заданная двумя или больше точками, которые можно представлять еще двумя переменными, latborder и lonborder. Когда построено вместе, две пары переменных могут сформировать карту. Закрашенная фигура Великобритании плюс линия, показывающая шотландскую границу, может быть похожей на две закрашенных фигуры или области, но нет никакого объекта, который представляет Англию и никакой объект, который представляет Шотландию, или в рабочей области или на осях карты.
Для того, чтобы представлять обе области правильно, многоугольник Великобритании должен быть разделен в двух точках, где граница соответствует ему, и копия latborder и lonborder конкатенированный к обеим линиям (помещающий один в обратном порядке). Получившиеся два многоугольника могут быть представлены отдельно (например, в четырех переменных под названием latengland, lonengland, latscotland, и lonscotland) или в двух переменных, которые задают два многоугольника каждый, очерченный NaNs (например, latuk, lonuk).
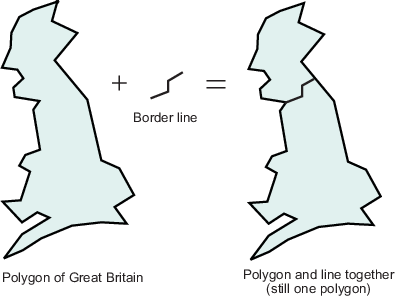
Различие между линией и данными о многоугольнике, может казаться, не важно, но это может иметь значение, когда вы выполняете географический анализ и тематическое отображение. Например, данные о многоугольнике могут быть обработаны как данные о линии и отображены с функциями такой как linem, но данные о линии не могут быть обработаны как многоугольники, если они не реструктурированы, чтобы сделать все объекты близко на себе, как описано в Линейных сегментах Ссылки с Общими Конечными точками в Многоугольники.