Изменение Alphamap
У каждой фигуры есть связанный alphamap, который является вектором из значений в пределах от от 0 до 1. Значение по умолчанию alphamap содержит 64 значения, располагающиеся линейно от 0 до 1. Просмотрите или измените alphamap использование Alphamap свойство фигуры или использования alphamap функция.
Альфа-карта по умолчанию
Значение по умолчанию alphamap содержит 64 значения, располагающиеся линейно от 0 до 1, как показано в следующем графике.
am = get(gcf,'Alphamap'); plot(am)
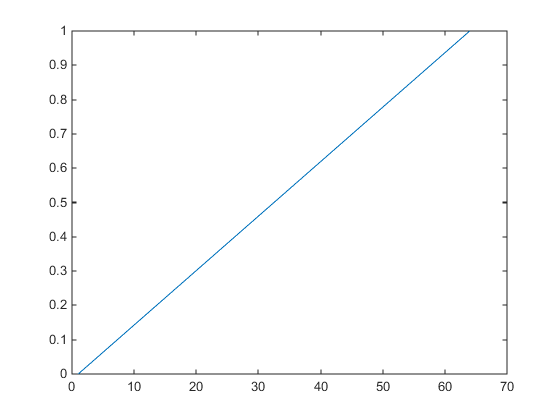
Этот alphamap отображает самые низкие альфа-значения данных, столь же абсолютно прозрачные и самые высокие альфа-значения данных как непрозрачный.
alphamap функция создает, некоторые полезные предопределили alphamaps и также позволяют вам изменить существующие карты. Например,
figure;
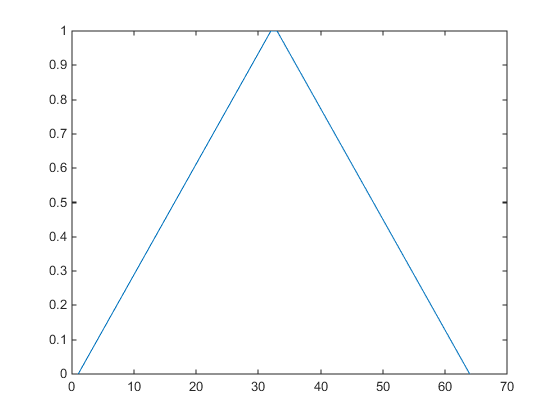
alphamap('vup')
устанавливает фигуру Alphamap свойство к alphamap, увеличение значений которого затем уменьшается:
am = get(gcf,'Alphamap');
plot(am)
Можно переключить значения с помощью increase или decrease опции. Например,
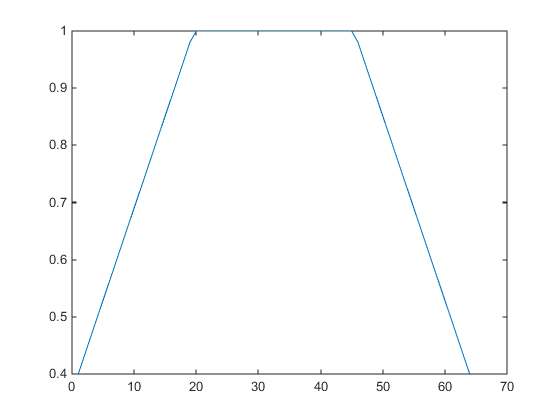
alphamap('increase',.4)
добавляет значение.4 ко всем значениям в alphamap текущей фигуры. Переграфический вывод 'vup' alphamap иллюстрирует изменение. Значения фиксируются к области значений [0 1].
am = get(gcf,'Alphamap'); plot(am)
Пример - изменение Alphamap
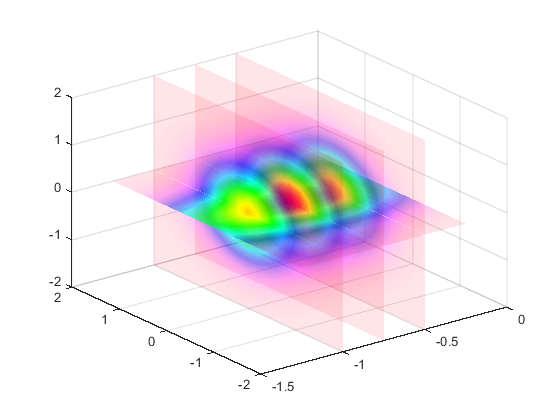
Этот пример использует плоскости разбиения, чтобы исследовать данные об объеме. Плоскости разбиения используют цветные данные для альфа-данных и используют rampdown alphamap (диапазон значений от 1 до 0):
Создайте данные об объеме путем выполнения функции трех переменных.
[x,y,z] = meshgrid(-1.25:.1:-.25,-2:.2:2,-2:.1:2); v = x.*exp(-x.^2-y.^2-z.^2);
Создайте плоскости разбиения, установите альфа-данные, равные цветным данным, и задайте, интерполировал
FaceColorиFaceAlpha.h = slice(x,y,z,v,[-1 -.75 -.5],[],[0]); set(h,'EdgeColor','none',... 'FaceColor','interp',... 'FaceAlpha','interp') alpha('color')Установите rampdown alphamap и увеличьте каждое значение в alphamap.1, чтобы достигнуть желаемой степени прозрачности. Задайте
hsvпалитра.alphamap('rampdown') alphamap('increase',.1) colormap hsv
Этот alphamap отображает наименьшие значения функции (вокруг нуля) с наименьшим количеством прозрачности и самым большим отображением значений с большей частью прозрачности. Это позволяет вам видеть через плоскости разбиения, одновременно сохраняя данные вокруг нуля.
