solvepde возвращает StationaryResults или TimeDependentResults возразите, чьи свойства содержат решение и его градиент в узлах mesh. Можно интерполировать решение и его градиент к другим точкам в геометрии при помощи interpolateSolution и evaluateGradient. Также можно вычислить поток решения в узлах mesh и в произвольных точках при помощи evaluateCGradient.
Примечание
solvepde не вычисляет компоненты потока решения для УЧП. Чтобы вычислить поток решения в узлах mesh, использовать evaluateCGradient.
solvepdeeig возвращает EigenResults возразите, чьи свойства содержат собственные вектора решения, вычисленные в узлах mesh. Можно интерполировать решение других точек при помощи interpolateSolution.
Размерности решения, его градиента и потока решения зависят от:
Количество геометрических точек оценки.
Для результатов, возвращенных solvepde или solvepdeeig, это - количество узлов mesh.
Для результатов, возвращенных interpolateSolution,evaluateGradient, и evaluateCGradient это - количество точек запроса.
Количество уравнений.
Для результатов, возвращенных solvepde или solvepdeeig, это - количество уравнений в системе.
Для результатов, возвращенных interpolateSolution,evaluateGradient, и evaluateCGradient, это - количество индексов уравнения запроса.
Число раз для зависящей от времени проблемы или количества режимов для задачи о собственных значениях.
Для результатов, возвращенных solvepde, это - номер времен решения (заданный как вход к solvepde).
Для результатов, возвращенных solvepdeeig, это - количество собственных значений.
Для результатов, возвращенных interpolateSolution, evaluateGradient, и evaluateCGradient, это - номер времени выполнения запроса для зависящих от времени проблем или режимов запроса для задач о собственных значениях.
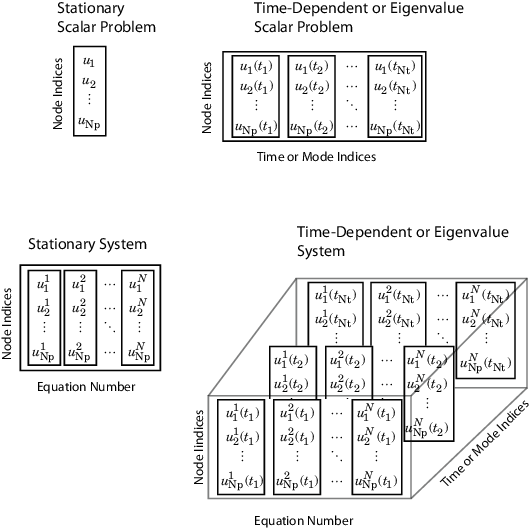
Предположим, что у вас есть проблема в который:
Np количество узлов в mesh.
Nt число раз для зависящей от времени проблемы или количества режимов для задачи о собственных значениях.
N количество уравнений в системе.
Предположим, что вы также вычисляете решение, его градиент или поток решения в других точках ("точки запроса") в геометрии при помощи interpolateSolution, evaluateGradient, или evaluateCGradient, соответственно. Здесь:
Nqp количество точек запроса.
Nqt номер времени выполнения запроса для зависящей от времени проблемы или количество режимов запроса для задачи о собственных значениях.
Nq количество индексов уравнений запроса.
Таблицы показывают, как индексировать в решение, возвращенное solvepde или solvepdeeig, где:
iP содержит индексы узлов.
iT содержит индексы времен для зависящей от времени проблемы или чисел режима для задачи о собственных значениях.
iN содержит индексы уравнений.
Таблицы также показывают размерности решений, градиентов и потока решения в узловых местоположениях (возвращенный solvepde,solvepdeeig, и evaluateCGradient) и размерности интерполированных решений и градиентов (возвращенный interpolateSolution, evaluateGradient, и evaluateCGradient).
| Стационарная проблема УЧП | Решение доступа и компоненты градиента | Размер NodalSolution, XGradients, YGradients, ZGradients, и компоненты потока в узлах | Размер решения, компоненты градиента и компоненты потока в точках запроса |
|---|---|---|---|
| Скаляр |
| Np- 1 | Nqp- 1 |
Система, N> 1 |
| Np- N | Nqp- N |
| Зависящая от времени проблема УЧП | Решение доступа и компоненты градиента | Размер NodalSolution, XGradients, YGradients, ZGradients, и компоненты потока в узлах | Размер решения, компоненты градиента и компоненты потока в точках запроса |
|---|---|---|---|
| Скаляр |
| Np- Nt | Nqp- Nqt |
Система, N> 1 |
| Np- N- Nt | Nqp- Nq- Nqt |
| Задача о собственных значениях УЧП | Доступ к собственным векторам | Размер Eigenvectors | Размер интерполированных собственных векторов |
|---|---|---|---|
| Скаляр |
| Np- Nt | Nqp- Nqt |
Система, N> 1 |
| Np- N- Nt | Nqp- Nq- Nqt |
EigenResults | evaluateGradient | interpolateSolution | solvepde | solvepdeeig | StationaryResults | TimeDependentResults