Это тематическое исследование объясняет, как создать вашу собственную библиотеку пользовательских блоков на основе файлов компонента. Это пользуется библиотекой в качестве примера конденсаторных моделей. Библиотека использует Основу Simscape™ электрическая область и задает три простых компонента. Для более усовершенствованных тем, включая добавление нескольких уровней иерархии, добавление новых областей и настройка внешнего вида библиотеки, видят Тематическое исследование — Электрохимическая Библиотека.
Библиотека в качестве примера приезжает созданная и в ваш путь так, чтобы это было с готовностью исполняемо. Однако рекомендуется, чтобы вы скопировали исходные файлы в новую директорию, для которой вы имеете разрешение записи и добавляете что директория в ваш путь MATLAB®. Это позволит вам вносить изменения и восстанавливать библиотеку для себя. Исходные файлы для библиотеки в качестве примера находятся в следующей директории пакета:
matlabroot/toolbox/physmod/simscape/simscapedemos/+Capacitors
где matlabroot корневой каталог MATLAB на вашей машине, как возвращено путем ввода
matlabroot
в командном окне MATLAB.
После копирования файлов измените имя каталога +Capacitors к другому имени, например, +MyCapacitors, так, чтобы ваша копия библиотеки создала с уникальным именем.
Чтобы создать библиотеку, ввести
ssc_build MyCapacitors
в командном окне MATLAB. При создании из +MyCapacitors директория пакета, можно не использовать аргумент и ввести только
ssc_build
Когда сборка завершится, откройте сгенерированную библиотеку путем ввода
MyCapacitors_lib
Для получения дополнительной информации о процессе сборки библиотеки смотрите Библиотеки Пользовательского блока Создания.
Чтобы добавить блок, запишите соответствующий файл компонента и поместите его в директорию пакета. Например, блок Ideal Capacitor в вашем MyCapacitors_lib библиотека производится IdealCapacitor.ssc файл. Откройте этот файл в редакторе MATLAB и исследуйте его содержимое.
component IdealCapacitor
% Ideal Capacitor
% Models an ideal (lossless) capacitor. The output current I is related
% to the input voltage V by I = C*dV/dt where C is the capacitance.
% Copyright 2008-2017 The MathWorks, Inc.
nodes
p = foundation.electrical.electrical; % +:top
n = foundation.electrical.electrical; % -:bottom
end
parameters
C = { 1, 'F' }; % Capacitance
end
variables
i = { 0, 'A' }; % Current
v = {value = { 0, 'V' }, priority = priority.high}; % Voltage drop
end
branches
i : p.i -> n.i; % Through variable i from node p to node n
end
equations
assert(C > 0)
v == p.v-n.v; % Across variable v from p to n
i == C*v.der; % Capacitor equation
end
end
Во-первых, давайте исследуем элементы файла компонента, которые влияют на внешний вид блока. Дважды кликните блок Ideal Capacitor в MyCapacitors_lib библиотека, чтобы открыть ее диалоговое окно и сравнить значок блока и диалоговое окно к содержимому IdealCapacitor.ssc файл. Имя блока, Идеальный Конденсатор, взято из комментария к линии 2. Комментарии к линиям 3 и 4 затем взяты, чтобы заполнить описание блока в диалоговом окне. Порты блока заданы разделом узлов. Выражения комментария в конце каждой линии управляют меткой порта и местоположением. Так же в разделе параметров, комментарии используются, чтобы задать названия параметра в диалоговом окне блока. Для получения дополнительной информации смотрите Настройку Имени блока и Внешнего вида.
Также заметьте, что в разделе уравнения существует утверждение, чтобы гарантировать, что значение емкости всегда больше нуля. Это - хорошая практика, чтобы гарантировать, что компонент не используется за пределами его области валидности. Библиотечным блокам Основы Simscape реализовали такие проверки, где это необходимо.
В этой библиотеке в качестве примера существует два дополнительных компонента, которые могут использоваться для моделирования суперконденсатора. Эти компоненты являются эволюциями Идеального Конденсатора. Это - хорошая практика, чтобы инкрементно создать модели компонента, добавляя и тестируя дополнительные функции, когда они добавляются.
Идеальный суперконденсатор

Суперконденсаторы, как их имя предполагает, являются конденсаторами с очень высоким значением емкости. Отношение между напряжением и зарядом не является постоянным, в отличие от этого, для идеального конденсатора. Предположим, что таблица данных производителя дает график емкости как функция напряжения, и та емкость увеличивается приблизительно линейно с напряжением от 1 фарады на уровне нулевых вольт к 1,5 фарадам, когда напряжение составляет 2,5 вольта. Если напряжение емкости обозначается v, то емкость может быть аппроксимирована как:
Для конденсатора, текущего i и напряжения v связаны стандартным уравнением
и следовательно
где C0 = 1 и Cv = 0.2. Это уравнение реализовано следующей линией в разделе уравнения файла Simscape IdealUltraCapacitor.ssc:
i == (C0 + Cv*v)*v.der;
Для программного обеспечения Simscape, чтобы интерпретировать это уравнение, переменные (v и i) и параметры (C0 и Cv) должен быть задан в разделе объявления. Для получения дополнительной информации смотрите, Объявляют Переменные Компонента и Объявляют Параметры Компонента.
Реализация некоторых уравнений компонента требует использования внутренних переменных. Пример при реализации суперконденсатора с резистивными потерями. Существует два резистивных условия, эффективное серийное сопротивление R и сопротивление саморазряда Rd. Из-за топологии это не возможно к непосредственно специальному конденсаторные уравнения в терминах через и через переменные i и v.
Суперконденсатор с резистивными потерями
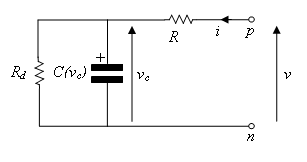
Этот блок реализован файлом компонента LossyUltraCapacitor.ssc. Откройте этот файл в редакторе MATLAB и исследуйте его содержимое.
component LossyUltraCapacitor
% Lossy Ultracapacitor
% Models an ultracapacitor with resistive losses. The capacitance C
% depends on the voltage V according to C = C0 + V*dC/dV. A
% self-discharge resistance is included in parallel with the capacitor,
% and an equivalent series resistance in series with the capacitor.
% Copyright 2008-2017 The MathWorks, Inc.
nodes
p = foundation.electrical.electrical; % +:top
n = foundation.electrical.electrical; % -:bottom
end
parameters
C0 = { 1, 'F' }; % Nominal capacitance C0 at V=0
Cv = { 0.2, 'F/V'}; % Rate of change of C with voltage V
R = {2, 'Ohm' }; % Effective series resistance
Rd = {500, 'Ohm' }; % Self-discharge resistance
end
variables
i = { 0, 'A' }; % Current
vc = {value = { 0, 'V' }, priority = priority.high}; % Capacitor voltage
end
branches
i : p.i -> n.i; % Through variable i from node p to node n
end
equations
assert(C0 > 0)
assert(R > 0)
assert(Rd > 0)
let
v = p.v-n.v; % Across variable v from p to n
in
i == (C0 + Cv*vc)*vc.der + vc/Rd; % Equation 1
v == vc + i*R; % Equation 2
end
end
end
Дополнительная переменная используется, чтобы обозначить напряжение через конденсатор, vc. Уравнения могут затем быть описаны в терминах v, i и vc с помощью тока Кирхгоффа и законов о напряжении. При подведении итогов токов в конденсаторе + узел дает первое уравнение Simscape:
i == (C0 + Cv*vc)*vc.der + vc/Rd;
Подведение итогов напряжений дает второе уравнение Simscape:
v == vc + i*R;
Как проверка, количество уравнений, требуемых для компонента, используемого в одной связанной сети, дано суммой количества портов плюс количество внутренних переменных минус одна. Это не обязательно верно для всех компонентов (например, одним исключением является масса), но в целом это - хорошее эмпирическое правило. Здесь это дает 2 + 1 - 1 = 2.
В файле Simscape начальное условие (начальное напряжение в этом примере) применяется к переменной vc с priority = priority.high, потому что это - дифференциальная переменная. В этом случае, vc с готовностью идентифицируется как дифференциальная переменная, когда она имеет der (дифференциатор) оператор применился к нему.
Конденсатор блокируется в библиотеке MyCapacitors_lib в качестве примера сопоставьте значки с ними.

Во время сборки библиотеки, если существует файл изображения в директории с тем же именем как файл компонента Simscape, то это используется, чтобы задать значок для блока. Например, блок Ideal Capacitor задан IdealCapacitor.ssc использует IdealCapacitor.jpg задавать его значок блока. Если вы не включаете файл изображения, то блок отображает свое имя вместо значка. Для получения дополнительной информации смотрите, Настраивают Значок Блока.