Приемники RF усиливают сигналы и переключают их, чтобы понизить частоты. Сам приемник вводит шум, который ухудшает полученный сигнал. Отношение сигнал-шум (SNR) в приемнике выход в конечном счете определяет удобство пользования приемника.
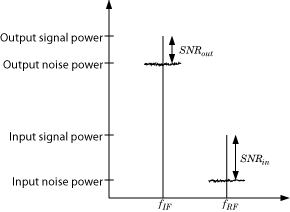
Предыдущая фигура иллюстрирует эффект приемника на сигнале. Приемник усиливает малую мощность сигнал RF в поставщике услуг fRF с высоким ОСШ и downconverts сигнал к fIF. Шумовая фигура (NF) системы определяет различие между ОСШ при выходе и ОСШ во входе:
где разность вычислена в децибелах. Чрезмерная шумовая фигура в системе заставляет шум сокрушать сигнал, делая сигнал неисправимым.
Модель ex_simrf_snr симулирует упрощенную архитектуру приемника IF. Блок Sinusoid и блок Noise моделируют двухцветный вход, сосредоточенный в fRF и низкоуровневом тепловом шуме. Система RF усиливает сигнал и смешивает его с локальным генератором fLO вниз к промежуточной частоте fIF. Датчик напряжения восстанавливает сигнал в IF.
Открыть эту модель, в командной строке MATLAB®, введите:
addpath(fullfile(docroot,'toolbox','simrf','examples')) ex_simrf_snr
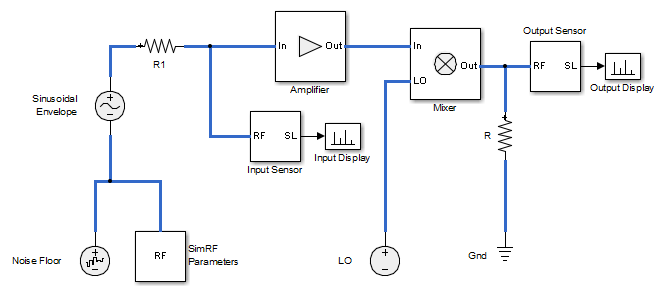
Усилитель вносит 40 дБ усиления и шумовой фигуры на 15 дБ, и микшер вносит 0 дБ усиления и шумовой фигуры на 20 дБ, которые являются характеристикой значений относительно шумного, приемника высокого усиления. Двухцветный вход имеет заданный уровень.1 μV. 1-V уровень в локальном генераторе гарантирует непротиворечивость формулировкой усиления преобразования микшера.
Запускать модель:
Откройте модель путем щелчка по ссылке или путем введения имени модели в подсказке Командного окна.
Нажмите Run.
Чтобы максимизировать эффективность, Fundamental tones и параметры Harmonic order задают частоты симуляции явным образом в блоке Configuration:
fLO, частота LO на первом этапе смешивания, равняется 1,9999 ГГц и появляется в списке основных тонов как carriers.LO.
fRF, поставщик услуг желаемого сигнала, равняется 2 ГГц и появляется в списке основных тонов как carriers.RF.
fIF, промежуточная частота, равняется fRF – fLO. Частота является линейной комбинацией (основных) гармоник первого порядка fLO и fRF. Установка Harmonic order к 1 достаточно, чтобы гарантировать, что эта частота появляется в частотах симуляции. Это минимальное значение для гармонического порядка гарантирует минимум частот симуляции.
Условия решателя и шумовые настройки также заданы для блока Configuration:
Solver type установлен в auto. Для получения дополнительной информации о выборе решателей смотрите страницу с описанием для блока Configuration или смотрите Решатели Simscape™ и Choosing Simulink®.
Параметр Sample time устанавливается на 1/(mod_freq*64). Эта установка гарантирует пропускную способность симуляции, в 64 раза больше, чем сигналы конверта в системе.
Флажок Simulate noise устанавливается, таким образом, среда включает шумовые параметры в процессе моделирования.
Модель использует подсистемы с реализацией MATLAB Coder™ быстрого преобразования Фурье (FFT), чтобы сгенерировать два графика. БПФ использует 64 интервала, таким образом, для частоты дискретизации 64 Гц, пропускная способность каждого интервала составляет 1 Гц. Впоследствии, уровни мощности, показанные на рисунках также, представляют степень спектральную плотность (PSD) сигналов в dBm/Hz.
Входной график Отображения показывает спектр мощности сигнала и шума во входе приемника.
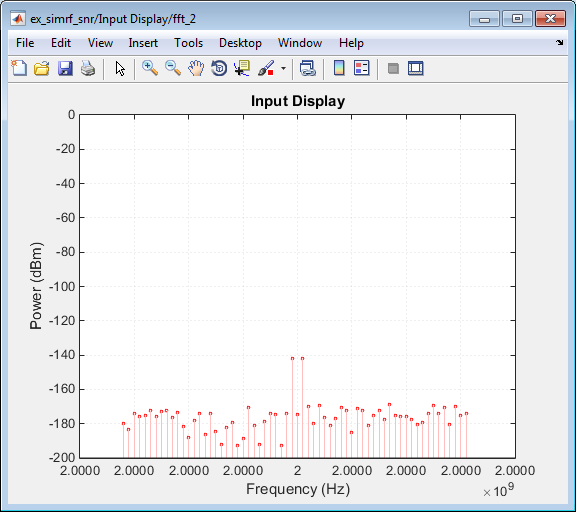
Измеренная степень каждого тона сопоставима с ожидаемым уровнем мощности 0.1-μV двухцветного конверта:
Фактор 1/2 происходит из-за деления напряжения через источник и нагрузочные резисторы, и другой фактор 1/2 происходит из-за масштабирования конверта. Смотрите известный пример Двухцветный Анализ Конверта Используя Действительные Сигналы для большего количества обсуждения масштабирующихся сигналов конверта для расчета мощности.
Измеренный уровень шума в -177 dBm/Hz уменьшается на 3 дБ от заданного уровня шума-174 dBm/Hz. Различие происходит из-за передачи степени от источника до входа усилителя. Усилитель также моделирует пол теплового шума, поэтому несмотря на то, что это уменьшение нереалистично, это не влияет на точность в выходном каскаде.
Выходной график Отображения показывает спектр мощности сигнала и шума при выходе приемника.
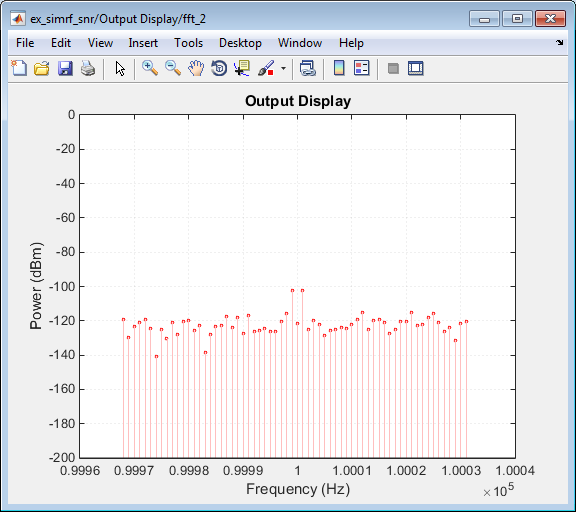
Измеренный PSD -102 dBm/Hz для каждого тона сопоставим с объединенным усилением на 40 дБ усилителя и микшера. Шумовой PSD на рисунке, как показывают, на приблизительно 50 дБ выше при выходе, из-за усиления и шумовой фигуры системы.
Если вам установили программное обеспечение DSP System Toolbox™, можно заменить подсистемы MATLAB Coder на блок Spectrum Analyzer (DSP System Toolbox).
Степень теплового шума может быть смоделирована согласно уравнению
где:
kB является константой Больцманна, равной 1,38065 × 10-23 J/K.
T является шумовой температурой в виде 293.15 K в этом примере.
Rs является импедансом источника шума в виде 50 Ω в этом примере, чтобы согласиться со значением сопротивления блока Resistor, пометил R1.
Δf является шумовой пропускной способностью.
Чтобы смоделировать уровень шума на сигнале RF в резисторе, модель включает блок Noise:
Параметр Noise Power Spectral Density (Watts/Hz) вычисляется как .
Параметр Carrier frequencies, набор к carriers.RF, шум мест на поставщике услуг RF только.
К шуму модели RF от шумовых фигур компонента:
Выберите Simulate noise в RF Blockset диалоговое окно блока Parameters, если это уже не выбрано.
Задайте значение для параметра Noise figure (dB) блоков Mixer и Amplifier.
Шумовые фигуры не являются строго аддитивными. Усилитель вносит больше шума в систему, чем микшер, потому что это появляется первым в каскаде. Чтобы вычислить общую шумовую фигуру системы RF с этапами n, используйте уравнение Friis:
где Fi и Gi являются шумовым фактором и усилением i th этап и NFi = 10log10 (Fi).
В этом примере шумовая фигура усилителя - 10 дБ, и шумовая фигура микшера - 15 дБ, таким образом, шумовая фигура системы:
Уравнение Friis показывает, что несмотря на то, что микшер имеет более высокую шумовую фигуру, усилитель вносит больше шума в систему.