Для неявных решателей Simulink® должен вычислить якобиан решателя, который является субматрицей якобиевской матрицы, сопоставленной с непрерывным представлением модели Simulink. В общем случае это непрерывное представление имеет форму:
Якобиан, J, сформированный из этой системы уравнений:
В свою очередь якобиан решателя является субматрицей, .
Для многих физических систем якобиан решателя Jx разрежен, означая, что многими элементами Jx является нуль.
Рассмотрите следующую систему уравнений:
От этой системы можно вывести шаблон разреженности, который отражает структуру уравнений. Шаблон, Булева матрица, имеет 1 для каждого это появляется явным образом на правой стороне уравнения. Поэтому вы получаете:
Разреженное возмущение и разреженные аналитические методы могут смочь использовать в своих интересах этот шаблон разреженности, чтобы сократить количество необходимых расчетов и улучшать производительность.
Когда вы выбираете неявный решатель из панели Solver диалогового окна параметров конфигурации, параметра под названием Solver Jacobian method и появляется выпадающее меню. Это меню имеет пять опций для вычисления якобиана решателя.
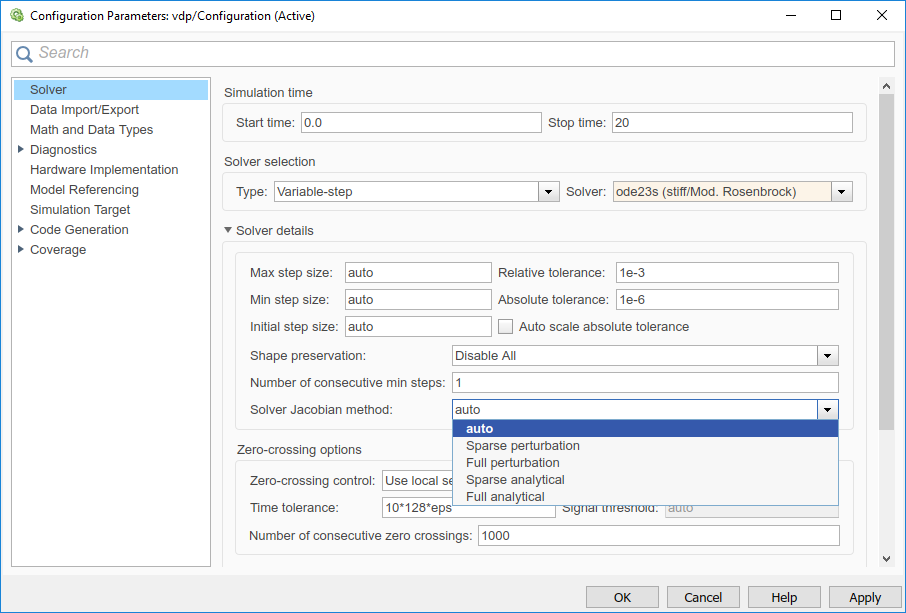
Примечание
Если вы устанавливаете Automatic solver parameter selection на error в панели Диагностики Решателя, и вы выбираете другой решатель, чем предложенный Simulink, можно получить ошибку.
Методам якобиана решателя сопоставили эти ограничения с ними.
Если вы выбираете аналитический якобиевский метод, но один или несколько блоков в модели не имеют аналитического якобиана, то Simulink применяет метод возмущения.
Если вы выбираете разреженное возмущение, и ваша модель содержит блоки хранилища данных, Simulink применяет полный метод возмущения.
Настройка по умолчанию для Solver Jacobian method auto. Выбор этого выбора заставляет Simulink определять, какой из остающихся четырех методов лучше всего удовлетворяет вашей модели. Эта блок-схема изображает алгоритм.
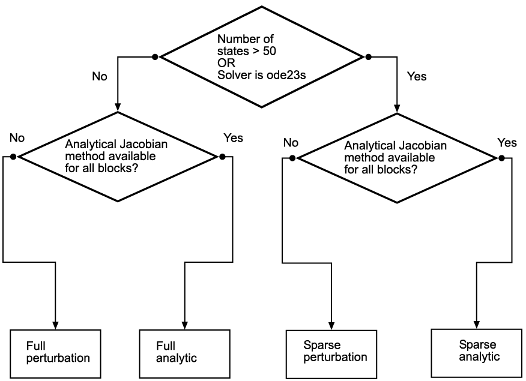
Разреженные методы выгодны для моделей, которые имеют большое количество состояний. Если 50 или больше состояний существуют в вашей модели, auto выбирает разреженный метод. В отличие от других неявных решателей, ode23s разреженный метод, потому что он генерирует новый якобиан на каждом временном шаге. Разреженное аналитическое или разреженный метод возмущения, поэтому, выгодны. Выбор auto также гарантирует, что аналитические методы используются, только если каждый блок в вашей модели может сгенерировать аналитический якобиан.
Полный метод возмущения решает полный набор уравнений возмущения и использует LAPACK для линейных алгебраических операций. Этот метод является дорогостоящим с вычислительной точки зрения, но остается рекомендуемый метод для установления базовых результатов.
Разреженный метод возмущения пытается улучшать производительность во время выполнения путем пользования преимуществами математическим премуществом разреженного якобиевского шаблона. Возврат демонстрационной системе трех уравнений и трех состояний,
Якобиан решателя:
|
Поэтому, необходимо встревожить каждое из трех состояний три раза и выполнить производную функцию три раза. Для системы с состояниями n этот метод тревожит состояния времена n.
Путем применения шаблона разреженности и беспокойства состояний x 1 и x 2 вместе, эта матрица уменьшает до:
|
Решатель может теперь решить столбцы 1 и 2 в одной развертке. В то время как разреженный метод возмущения сохраняет значительный расчет, он также добавляет наверху к компиляции. Это может даже замедлить симуляцию, если система не имеет большого количества непрерывных состояний. Переломный момент существует, для которого вы получаете увеличенную эффективность путем применения этого метода. В общем случае системы, имеющие большое количество непрерывных состояний, обычно разреженны и преимущество из разреженного метода.
Разреженный метод возмущения, как разреженный аналитический метод, использует UMFPACK, чтобы выполнить линейные алгебраические операции. Кроме того, разреженный метод возмущения поддерживает и RSim и быстрый режим Accelerator.
Полные и разреженные аналитические методы пытаются улучшать производительность путем вычисления якобиевских использующих аналитических уравнений, а не уравнений возмущения. Разреженный аналитический метод, также использует информацию о разреженности, чтобы ускорить линейные алгебраические операции, требуемые решить обыкновенные дифференциальные уравнения.
Для получения дополнительной информации о том, как получить доступ и интерпретировать шаблон разреженности в MATLAB®, смотрите Исследование Структуры якобиана Решателя Модели.
В то время как разреженный метод возмущения поддерживает RSim, разреженный аналитический метод не делает. Следовательно, независимо от которого разреженного метода вы выбираете, любой сгенерированный код использует разреженный метод возмущения. Это ограничение применяется к быстрому режиму Accelerator также.