Exponenta Banner

Решите разностные уравнения Используя Z-преобразование

Решите разностные уравнения при помощи Z-преобразований в Symbolic Math Toolbox™ с этим рабочим процессом. Для простых примеров на Z-преобразовании смотрите ztrans и iztrans.

Определение: Z-преобразование

Z-преобразование функционального f (n) задано как

F(z)=∑n=0∞f(n)zn.

Концепция: Используя символьные рабочие процессы

Символьные рабочие процессы сохраняют вычисления в естественной символьной форме вместо числовой формы. Этот подход помогает вам изучить свойства своего решения и использовать точные символьные значения. Вы заменяете числами вместо символьных переменных только, когда вы требуете числового результата, или вы не можете продолжить символически. Для получения дополнительной информации смотрите, Выбирают Numeric or Symbolic Arithmetic. Как правило, шаги:

  1. Объявите уравнения.

  2. Решите уравнения.

  3. Замените значениями.

  4. Постройте результаты.

  5. Анализ результатов.

Рабочий процесс: решите "задачу" роста кролика Используя Z-преобразование

Объявите уравнения

Можно использовать Z-преобразование, чтобы решить разностные уравнения, такие как известная "проблема" Роста Кролика. Если пара кроликов назревает за один год, и затем производит другую пару кроликов каждый год, популяция кроликов p (n) в год, n описан этим разностным уравнением.

p (n +2) = p (n +1) + p (n).

Объявите уравнение как выражение, принимающее, что правой стороной является 0. Поскольку n представляет годы, примите тот n положительное целое число. Это предположение упрощает результаты.

syms p(n) z
assume(n>=0 & in(n,'integer'))
f = p(n+2) - p(n+1) - p(n)
f =
p(n + 2) - p(n + 1) - p(n)

Решите уравнения

Найдите Z-преобразование уравнения.

fZT = ztrans(f,n,z)
fZT =
z*p(0) - z*ztrans(p(n), n, z) - z*p(1) + z^2*ztrans(p(n), n, z) - ...
        z^2*p(0) - ztrans(p(n), n, z)

Функция solve решает только для символьных переменных. Поэтому использовать solve, сначала замените ztrans(p(n),n,z) с переменными pZT.

syms pZT
fZT = subs(fZT,ztrans(p(n),n,z),pZT)
fZT =
z*p(0) - pZT - z*p(1) - pZT*z - z^2*p(0) + pZT*z^2

Решите для pZT.

pZT = solve(fZT,pZT)
pZT =
-(z*p(1) - z*p(0) + z^2*p(0))/(- z^2 + z + 1)

Вычислите p (n) путем вычисления обратного Z-преобразования pZT. Упростите результат.

pSol = iztrans(pZT,z,n);
pSol = simplify(pSol)
pSol =
2*(-1)^(n/2)*cos(n*(pi/2 + asinh(1/2)*1i))*p(1) + ...
                 (2^(2 - n)*5^(1/2)*(5^(1/2) + 1)^(n - 1)*(p(0)/2 - p(1)))/5 - ...
                 (2*2^(1 - n)*5^(1/2)*(1 - 5^(1/2))^(n - 1)*(p(0)/2 - p(1)))/5

Замените значениями

Чтобы построить результат, сначала замените значениями начальных условий. Позвольте p(0) и p(1) будьте 1 и 2, соответственно.

pSol = subs(pSol,[p(0) p(1)],[1 2])
pSol =
4*(-1)^(n/2)*cos(n*(pi/2 + asinh(1/2)*1i)) - (3*2^(2 - n)*5^(1/2)* ...
    (5^(1/2) + 1)^(n - 1))/10 + (3*2^(1 - n)*5^(1/2)*(1 - 5^(1/2))^(n - 1))/5

Постройте результаты

Покажите рост в популяции кроликов в зависимости от времени путем графического вывода pSol.

nValues = 1:10;
pSolValues = subs(pSol,n,nValues);
pSolValues = double(pSolValues);
pSolValues = real(pSolValues);
stem(nValues,pSolValues)
title('Rabbit Population')
xlabel('Years (n)')
ylabel('Population p(n)')
grid on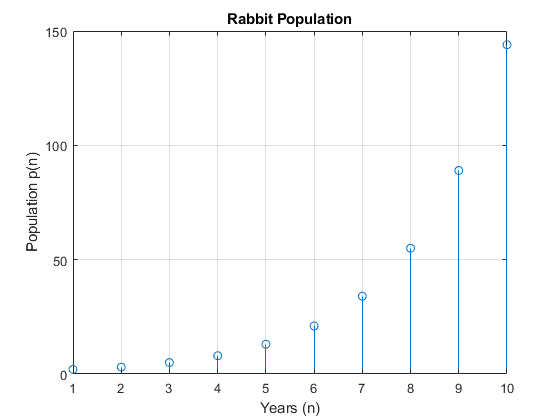

Анализ результатов

График показывает, что решение, кажется, увеличивается экспоненциально. Однако, потому что решение pSol содержит много условий, находя условия, которые производят это поведение, требует анализа.

Поскольку все функции в pSol может быть описан в терминах exp, перепишите pSol к exp. Упростите результат при помощи simplify с 80 дополнительные шаги упрощения. Теперь можно анализировать pSol.

pSol = rewrite(pSol,'exp');
pSol = simplify(pSol,'Steps',80)
pSol =
(2*2^n)/(- 5^(1/2) - 1)^n - (3*5^(1/2)*(1/2 - 5^(1/2)/2)^n)/10 + ...
    (3*5^(1/2)*(5^(1/2)/2 + 1/2)^n)/10 - (3*(1/2 - 5^(1/2)/2)^n)/2 + ...
    (5^(1/2)/2 + 1/2)^n/2

Визуально смотрите pSol. Заметьте тот pSol сумма условий. Каждый термин является отношением, которое может увеличиться или уменьшиться как n увеличения. Для каждого термина можно подтвердить эту гипотезу несколькими способами:

  • Проверяйте если предел в n = Inf переходит к 0 или Inf при помощи limit.

  • Постройте термин для увеличения n и проверяйте поведение.

  • Вычислите значение в большом значении n.

Для простоты используйте третий подход. Вычислите условия в n = 100, и затем проверьте подход. Во-первых, найдите отдельные условия при помощи children, замените n, и преобразуйте, чтобы удвоиться.

pSolTerms = children(pSol);
pSolTermsDbl = subs(pSolTerms,n,100);
pSolTermsDbl = double(pSolTermsDbl)
pSolTermsDbl =
   1.0e+20 *
    0.0000   -0.0000    5.3134   -0.0000    3.9604

Результат показывает, что некоторыми условиями является 0 в то время как другие условия имеют большую величину. Выдвиньте гипотезу, что условия большой величины производят экспоненциальное поведение. Аппроксимированный pSol с этими условиями.

idx = abs(pSolTermsDbl)>1; % use arbitrary cutoff
pApprox = pSolTerms(idx);
pApprox = sum(pApprox)
pApprox =
(3*5^(1/2)*(5^(1/2)/2 + 1/2)^n)/10 + (5^(1/2)/2 + 1/2)^n/2

Проверьте гипотезу путем графического вывода ошибки приближения между pSol и pApprox. Как ожидалось ошибка переходит к 0 как n увеличения. Этот результат демонстрирует, как символьные вычисления помогают вам анализировать свою проблему.

Perror = pSol - pApprox;
nValues = 1:30;
Perror = subs(Perror,n,nValues);
stem(nValues,Perror)
xlabel('Years (n)')
ylabel('Error (pSol - pApprox)')
title('Error in Approximation')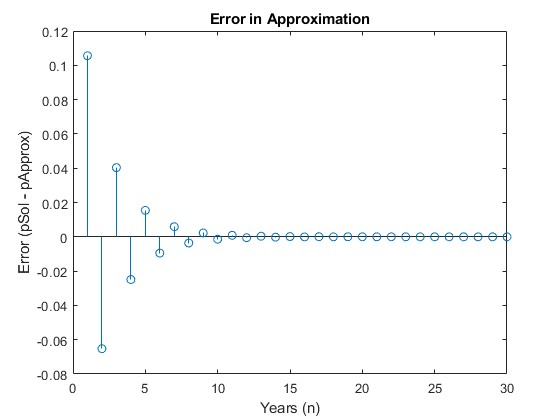

Ссылки

[1] Эндрюс, L.C., Shivamoggi, B.K., интеграл преобразовывает для инженеров и прикладных математиков, издательства Макмиллана, Нью-Йорк, 1986

[2] Crandall, R.E., проекты в научных расчетах, издателях Springer-Verlag, Нью-Йорк, 1994

[3] Странг, G., введение в прикладную математику, Wellesley-Кембриджское нажатие, Веллесли, MA, 1986

Документация Symbolic Math Toolbox

Поддержка