Exponenta Banner
exponenta event banner

Числовая модель обратной связи SISO

В этом примере показано, как соединить числовые модели LTI, представляющие несколько компонентов системы, чтобы создать одну числовую модель системы с обратной связью, с помощью арифметики модели и соединительных команд.

Создайте модель следующей одноконтурной системы управления.

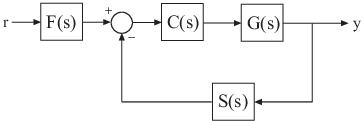
Обратная связь включает объект G (s), контроллер C (s) и представление динамики датчика, S (s). Система также включает предварительный фильтр F (s).

  1. Создайте объекты модели, представляющие каждый из компонентов.

    G = zpk([],[-1,-1],1);
C = pid(2,1.3,0.3,0.5);
S = tf(5,[1 4]);
F = tf(1,[1 1]);

    Объект G является нулями, полюсами и усилением (zpk) модель с двойным полюсом в s = –1. Объект модели C является ПИД-регулятором. Модели F и S являются передаточными функциями.

  2. Соедините контроллер и модель объекта управления.

    H = G*C;

    Объединить модели с помощью оператора умножения *, введите модели в обратном порядке по сравнению с блок-схемой.

    Совет

    В качестве альтернативы создайте H (s) с помощью series команда: 

    H = series(C,G);

  3. Создайте неотфильтрованный ответ с обратной связью T(s)=H1+HS.

    T = feedback(H,S);

    Внимание

    Не используйте арифметику модели, чтобы создать T алгебраически:

    T = H/(1+H*S)

    Это вычисление копирует полюса H, который увеличивает порядок модели и может привести к вычислительной погрешности.

  4. Создайте целый отклик системы с обратной связью от r до y.

    T_ry = T*F;

T_ry Числовая Модель LTI представление совокупной системы с обратной связью. T_ry не отслеживает коэффициенты компонентов GCF, и S.

Можно работать с T_ry с любой системой управления Control System Toolbox™ или аналитическими командами.

Смотрите также

| | |

Связанные примеры

Больше о

Документация Control System Toolbox

Поддержка