Программное обеспечение Curve Fitting Toolbox™ позволяет вам вычислить доверительные границы для подходящих коэффициентов и границы предсказания для новых наблюдений или для подходящей функции. Кроме того, для границ предсказания, можно вычислить одновременные границы, которые учитывают все значения предиктора, или можно вычислить неодновременные границы, которые учитывают только отдельные значения предиктора. Содействующие доверительные границы представлены численно, в то время как границы предсказания отображены графически и также доступны численно.
Доступное доверие и границы предсказания получены в итоге ниже.
Типы границ доверия и предсказания
IntervalType | Описание |
|---|---|
Подходящие коэффициенты | Доверительные границы для подходящих коэффициентов |
Новое наблюдение | Предсказание ограничивает для нового наблюдения (значение отклика) |
Новая функция | Предсказание ограничивает для нового значения функции |
Примечание
Границы предсказания также часто описываются как доверительные границы, потому что вы вычисляете доверительный интервал для предсказанного ответа.
Доверие и границы предсказания задают нижние значения и верхние значения связанного интервала, и задают ширину интервала. Ширина интервала указывает, насколько сомнительный вы о подходящих коэффициентах, предсказанном наблюдении или предсказанной подгонке. Например, очень широкий интервал для подходящих коэффициентов может указать, что необходимо использовать больше данных при подборе кривой, прежде чем можно будет сказать что-либо очень определенное в коэффициентах.
Границы заданы с уровнем уверенности, которую вы задаете. Уровень уверенности часто - 95%, но это может быть любое значение, такое как 90%, 99%, 99,9%, и так далее. Например, вы можете хотеть взять 5%-й шанс того, чтобы быть неправильным о предсказании нового наблюдения. Поэтому вы вычислили бы 95%-й интервал предсказания. Этот интервал указывает, что у вас есть 95%-й шанс, что новое наблюдение на самом деле содержится в более низких и верхних границах предсказания.
Доверительными границами для подходящих коэффициентов дают
где b является коэффициентами, произведенными подгонкой, t зависит от доверительного уровня и вычисляется с помощью инверсии кумулятивной функции распределения t Студента, и S является вектором из диагональных элементов от предполагаемой ковариационной матрицы содействующих оценок, (XTX) –1s2. В линейной подгонке X является матрицей проекта, в то время как для нелинейного подходящего X якобиан подходящих значений относительно коэффициентов. XT является транспонированием X, и s 2 является среднеквадратической ошибкой.
Доверительные границы отображены в панели Результатов в приложении Curve Fitting с помощью следующего формата.
p1 = 1.275 (1.113, 1.437)
Подходящее значение для коэффициента p1 1.275, нижняя граница 1.113, верхняя граница 1.437, и ширина интервала 0.324. По умолчанию доверительный уровень для границ составляет 95%.
Можно вычислить доверительные интервалы в командной строке с confint функция.
Как упомянуто ранее, можно вычислить границы предсказания для кривой по экспериментальным точкам. Предсказание основано на существующей подгонке к данным. Кроме того, границы могут быть одновременными и измерить доверие для всех значений предиктора, или они могут быть неодновременными и измерить доверие только для одного предопределенного значения предиктора. Если вы предсказываете новое наблюдение, неодновременные границы измеряют доверие, что новое наблюдение находится в интервале, учитывая одно значение предиктора. Одновременные границы измеряют доверие, что новое наблюдение находится в интервале независимо от значения предиктора.
| Связанный тип | Наблюдение | Функциональный |
|---|---|---|
| Одновременный |
|
|
| Неодновременный |
|
|
Где:
s 2 является среднеквадратической ошибкой
t зависит от доверительного уровня и вычисляется с помощью инверсии кумулятивной функции распределения t Студента
f зависит от доверительного уровня и вычисляется с помощью инверсии кумулятивной функции распределения F.
S является ковариационной матрицей содействующих оценок, (XTX) –1s2.
x является вектором-строкой из матрицы проекта или якобиана, оцененного в заданном значении предиктора.
Можно графически отобразить границы предсказания с помощью приложения Curve Fitting. С приложением Curve Fitting можно отобразить неодновременные границы предсказания для новых наблюдений с Tools> Prediction Bounds. По умолчанию доверительный уровень для границ составляет 95%. Можно изменить этот уровень в любое значение с Tools> Prediction Bounds> Custom.
Можно отобразить числовые границы предсказания любого типа в командной строке с predint функция.
Чтобы изучить количества, сопоставленные с каждым типом интервала предсказания, вспомните, что данные, подгонка и остаточные значения связаны через формулу
данные = соответствуют + остаточные значения
где подгонка и условия остаточных значений являются оценками условий в формуле
данные = модель + случайная ошибка
Предположим, что вы планируете взять новое наблюдение в значении предиктора x n +1. Вызовите новое наблюдение y n +1 (x n +1) и связанная ошибка ε n +1. То
y n +1 (x n +1) = f (x n +1) + ε n +1
где f (x n +1) является истинной, но неизвестной функцией, вы хотите оценить в x n +1. Вероятные значения для нового наблюдения или для предполагаемой функции введены неодновременными границами предсказания.
Если вместо этого вы хотите, чтобы вероятное значение нового наблюдения было сопоставлено со значением предиктора, предыдущее уравнение становится
y n +1 (x) = f (x) + ε
Вероятные значения для этого нового наблюдения или для предполагаемой функции введены одновременными границами предсказания.
Типы границ предсказания получены в итоге ниже.
Типы границ предсказания
Тип связанных | Одновременный или неодновременный | Связанное уравнение |
|---|---|---|
Наблюдение | Неодновременный | y n +1 (x n +1) |
Одновременный | y n +1 (x), для всего x | |
Функция | Неодновременный | f (x n +1) |
Одновременный | f (x), для всего x |
Неодновременные и одновременные границы предсказания для нового наблюдения и подходящей функции показывают ниже. Каждый график содержит три кривые: подгонка, более низкие доверительные границы и верхние доверительные границы. Подгонка является экспоненциалом одно термина к сгенерированным данным, и границы отражают 95%-й доверительный уровень. Обратите внимание на то, что интервалы, сопоставленные с новым наблюдением, более широки, чем подходящие функциональные интервалы из-за дополнительной неопределенности в предсказании нового значения отклика (кривая плюс случайные ошибки).
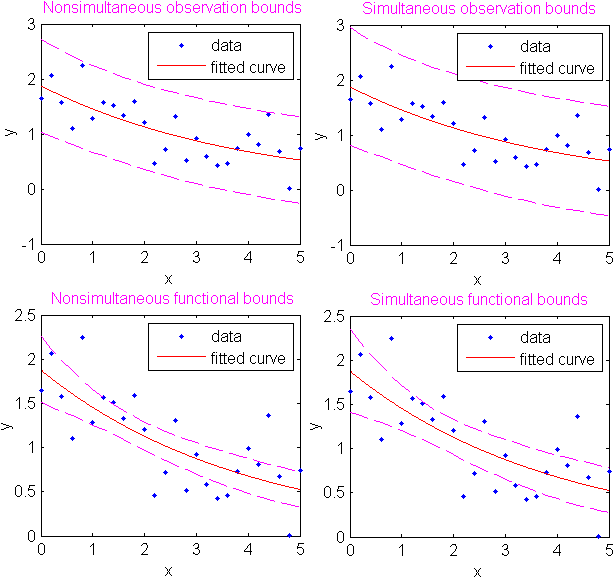
Вычислите и постройте наблюдение и функциональные интервалы предсказания для подгонки к зашумленным данным.
Сгенерируйте зашумленные данные с экспоненциальным трендом.
x = (0:0.2:5)'; y = 2*exp(-0.2*x) + 0.5*randn(size(x));
Соответствуйте кривой к данным с помощью экспоненциала одно термина.
fitresult = fit(x,y,'exp1');Вычислите 95%-е наблюдение и функциональные интервалы предсказания, и одновременные и неодновременные. Неодновременные границы для отдельных элементов x; одновременные границы для всех элементов x.
p11 = predint(fitresult,x,0.95,'observation','off'); p12 = predint(fitresult,x,0.95,'observation','on'); p21 = predint(fitresult,x,0.95,'functional','off'); p22 = predint(fitresult,x,0.95,'functional','on');
Отобразите на графике данные, подгонку и интервалы предсказания. Границы наблюдения более широки, чем функциональные границы, потому что они измеряют неопределенность в предсказании кривой по экспериментальным точкам плюс случайное изменение нового наблюдения.
subplot(2,2,1) plot(fitresult,x,y), hold on, plot(x,p11,'m--'), xlim([0 5]), ylim([-1 5]) title('Nonsimultaneous Observation Bounds','FontSize',9) legend off subplot(2,2,2) plot(fitresult,x,y), hold on, plot(x,p12,'m--'), xlim([0 5]), ylim([-1 5]) title('Simultaneous Observation Bounds','FontSize',9) legend off subplot(2,2,3) plot(fitresult,x,y), hold on, plot(x,p21,'m--'), xlim([0 5]), ylim([-1 5]) title('Nonsimultaneous Functional Bounds','FontSize',9) legend off subplot(2,2,4) plot(fitresult,x,y), hold on, plot(x,p22,'m--'), xlim([0 5]), ylim([-1 5]) title('Simultaneous Functional Bounds','FontSize',9) legend({'Data','Fitted curve', 'Prediction intervals'},... 'FontSize',8,'Location','northeast')
