Экспоненциальные модели

Об экспоненциальных моделях

Тулбокс обеспечивает один термин и модель экспоненциала 2D термина, как дано

$\begin{array}{l} y = a e^{b x} \\ y = a e^{b x} + c e^{d x} \end{array}$

Экспоненциалы часто используются, когда скорость изменения количества пропорциональна начальной сумме количества. Если коэффициент, сопоставленный с b и/или d, отрицателен, y представляет экспоненциальное затухание. Если коэффициент положителен, y представляет экспоненциальный рост.

Например, один радиоактивный режим затухания нуклида описан экспоненциалом с одним термином. a интерпретирован как начальное количество ядер, b является постоянным затуханием, x время, и y является количеством остающихся ядер после того, как определенное количество времени передает. Если два режима затухания существуют, то необходимо использовать модель экспоненциала 2D термина. Для второго режима затухания вы добавляете другой экспоненциальный термин в модель.

Примеры экспоненциального роста включают заразные болезни, для которых средство исправления является недоступными, и биологическими популяциями, рост которых свободен хищничеством, факторами окружающей среды, и так далее.

Подбирайте экспоненциальные модели в интерактивном режиме

Откройте приложение Curve Fitting путем ввода cftool. В качестве альтернативы нажмите Curve Fitting на вкладке Apps.
В приложении Curve Fitting выберите данные о кривой (X data и Y data, или только Y data против индекса).
Приложение Curve Fitting создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели от Polynomial к Exponential.

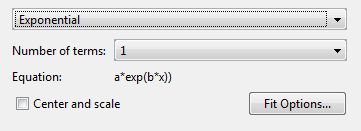
Можно задать следующие опции:

Выберите одно или два условия, чтобы соответствовать exp1 или exp2.
Посмотрите в панели Results, чтобы видеть условия модели, значения коэффициентов и статистику качества подгонки.
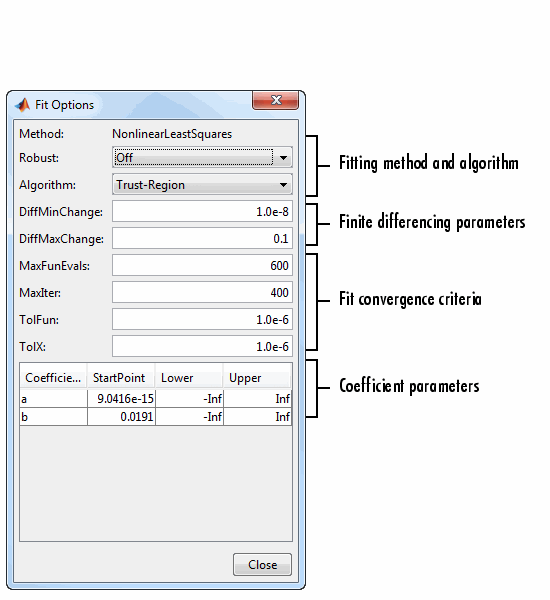
(Необязательно) Нажмите Fit Options, чтобы задать содействующие начальные значения и ограничительные границы, подходящие для ваших данных, или изменить настройки алгоритма.
Тулбокс вычисляет оптимизированные стартовые точки для экспоненциальных приближений, на основе текущего набора данных. Можно заменить стартовые точки и задать собственные значения в Подходящем Окне параметров.
Подходящие варианты для одно термина экспоненциал показываются затем. Содействующие начальные значения и ограничения для данных о переписи.

Для примера, задающего начальные значения, соответствующие данным, смотрите Гауссов Подбор кривой Экспоненциальным Фоном.
Для получения дополнительной информации о настройках см. Опции Подгонки Определения и Оптимизированные Начальные точки.

Подбирайте Экспоненциальные Модели Используя подходящую Функцию

Скрипт Open Live Script

В этом примере показано, как подбирать экспоненциальную модель к данным с помощью fit функция.

Экспоненциальная модель библиотеки является входным параметром к fit и fittype функции. Задайте тип модели 'exp1' или 'exp2' .

Подбирайте модель экспоненциала Одно Термина

Сгенерируйте данные с экспоненциальным трендом и затем соответствуйте данным с помощью экспоненциала одно термина. Постройте подгонку и данные.

x = (0:0.2:5)';
y = 2*exp(-0.2*x) + 0.1*randn(size(x));
f = fit(x,y,'exp1')

f = 
     General model Exp1:
     f(x) = a*exp(b*x)
     Coefficients (with 95% confidence bounds):
       a =       2.021  (1.89, 2.151)
       b =     -0.1812  (-0.2104, -0.152)

plot(f,x,y)

Figure contains an axes. The axes contains 2 objects of type line. These objects represent data, fitted curve.

Подбирайте модель экспоненциала 2D термина

f2 = fit(x,y,'exp2')

f2 = 
     General model Exp2:
     f2(x) = a*exp(b*x) + c*exp(d*x)
     Coefficients (with 95% confidence bounds):
       a =        2443  (-1.229e+12, 1.229e+12)
       b =     -0.2574  (-1.87e+04, 1.87e+04)
       c =       -2441  (-1.229e+12, 1.229e+12)
       d =     -0.2575  (-1.872e+04, 1.872e+04)

plot(f2,x,y)

Figure contains an axes. The axes contains 2 objects of type line. These objects represent data, fitted curve.

Установите стартовые точки

Тулбокс вычисляет оптимизированные стартовые точки для экспоненциальных приближений на основе текущего набора данных. Можно заменить стартовые точки и задать собственные значения.

Найдите порядок записей для коэффициентов в первой модели (f ) при помощи coeffnames функция.

coeffnames(f)

ans = 2x1 cell
    {'a'}
    {'b'}

Если вы задаете стартовые точки, выбираете значения, соответствующие вашим данным. Установите произвольные стартовые точки для коэффициентов a и b например, цели.

f = fit(x,y,'exp1','StartPoint',[1,2])

f = 
     General model Exp1:
     f(x) = a*exp(b*x)
     Coefficients (with 95% confidence bounds):
       a =       2.021  (1.89, 2.151)
       b =     -0.1812  (-0.2104, -0.152)

plot(f,x,y)

Figure contains an axes. The axes contains 2 objects of type line. These objects represent data, fitted curve.

Исследуйте опции экспоненциального приближения

Исследуйте подходящие опции, если вы хотите изменить подходящие опции, такие как содействующие начальные значения и ограничительные границы, подходящие для ваших данных, или изменить настройки алгоритма. Для получения дополнительной информации на этих опциях, см. таблицу свойств для NonlinearLeastSquares на fitoptions страница с описанием.

fitoptions('exp1')

ans =

        Normalize: 'off'
          Exclude: []
          Weights: []
           Method: 'NonlinearLeastSquares'
           Robust: 'Off'
       StartPoint: [1x0 double]
            Lower: [1x0 double]
            Upper: [1x0 double]
        Algorithm: 'Trust-Region'
    DiffMinChange: 1.0000e-08
    DiffMaxChange: 0.1000
          Display: 'Notify'
      MaxFunEvals: 600
          MaxIter: 400
           TolFun: 1.0000e-06
             TolX: 1.0000e-06

Смотрите также

fit | fitoptions | fittype

Документация