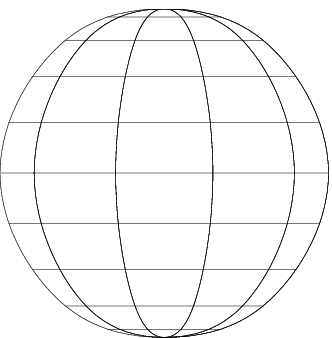
Сплайны с векторным знаком также используются в приближении к данным с координатной сеткой, в любом количестве переменных, с помощью сплайнов продукта тензора. Те же команды конструкции сплайна используются, только форма входа отличается. Например, если x m- вектор, y n- вектор и z массив размера [m,n], затем cs = csapi({x,y},z); описывает сплайн bicubic f, удовлетворяющий f (x (i), y (j)) =z (i, j) для i =1:m, j =1:n. Такой многомерный сплайн может быть с векторным знаком. Например,
x = 0:4; y=-2:2; s2 = 1/sqrt(2);
z(3,:,:) = [0 1 s2 0 -s2 -1 0].'*[1 1 1 1 1];
z(2,:,:) = [1 0 s2 1 s2 0 -1].'*[0 1 0 -1 0];
z(1,:,:) = [1 0 s2 1 s2 0 -1].'*[1 0 -1 0 1];
sph = csape({x,y},z,{'clamped','periodic'});
fnplt(sph), axis equal, axis off
дает совершенно приемлемую сферу. Его проекция на 
- плоскость построена по
Оба графика показывают ниже.
Сфера, сделанная двумерным сплайном продукта Tensor с 3-D знаком
Плоская проекция сферы сплайна
