Остаточные значения подобранной модели заданы как различия между данными об ответе и подгонкой к данным об ответе в каждом значении предиктора.
невязка = данные – подгонка
Вы отображаете остаточные значения в приложении Curve Fitting путем выбора кнопки на панели инструментов или пункта меню View> Residuals Plot.
Математически, невязка для определенного значения предиктора является различием между значением отклика y и предсказанным значением отклика ŷ.
r = y – ŷ
Принятие модели, которую вы подбираете к данным, правильно, остаточные значения аппроксимируют случайные ошибки. Поэтому, если остаточные значения, кажется, ведут себя случайным образом, это предполагает, что модель соответствует данным хорошо. Однако, если остаточные значения отображают систематический шаблон, это - ясный знак, что модель соответствует данным плохо. Всегда принимайте во внимание, что много результатов подбора кривой модели, таких как доверительные границы, будут недопустимы, должен модель быть чрезвычайно несоответствующим для данных.
Графический дисплей остаточных значений для первой аппроксимации полиномом степени показывают ниже. Главный график показывает, что остаточные значения вычисляются как вертикальное расстояние от точки данных до кривой по экспериментальным точкам. Нижний график отображает остаточные значения относительно подгонки, которая является нулевой линией.
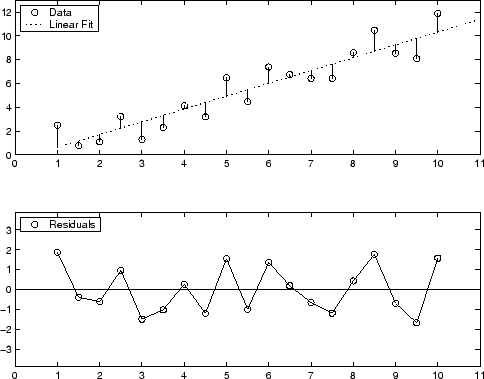
Остаточные значения кажутся случайным образом рассеянными вокруг нуля, указывающего, что модель описывает данные хорошо.
Графический дисплей остаточных значений для аппроксимации полиномом второй степени показывают ниже. Модель включает только квадратичный термин и не включает линейный или постоянный термин.
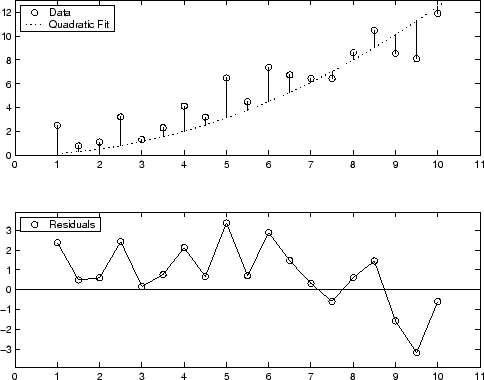
Остаточные значения систематически положительны для большой части области значений данных, указывающей, что эта модель является бедными, в форме для данных.
Этот пример подбирает несколько полиномиальных моделей к сгенерированным данным и оценивает, как хорошо те модели соответствуют данным и как точно они могут предсказать. Данные сгенерированы от кубической кривой, и существует большой разрыв в области значений переменной x, где никакие данные не существуют.
x = [1:0.1:3 9:0.1:10]'; c = [2.5 -0.5 1.3 -0.1]; y = c(1) + c(2)*x + c(3)*x.^2 + c(4)*x.^3 + (rand(size(x))-0.5);
Приспособьте данные в приложении Curve Fitting с помощью кубического полинома и пятого полинома степени. Данные, подгонки и остаточные значения показывают ниже. Отобразите остаточные значения в приложении Curve Fitting путем выбора View> Residuals Plot.
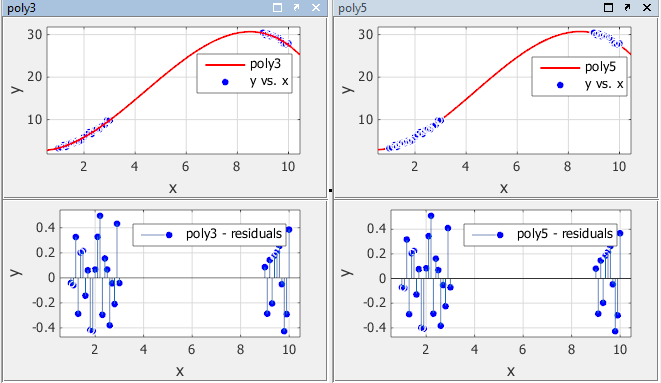
Обе модели, кажется, соответствуют данным хорошо, и остаточные значения, кажется, случайным образом распределяются вокруг нуля. Поэтому графическая оценка подгонок не показывает очевидных различий между этими двумя уравнениями.
Посмотрите на числовые результаты подгонки в Results, разделяют на области и сравнивают доверительные границы для коэффициентов.
Результаты показывают, что коэффициенты кубического соответствия точно известны (границы малы), в то время как коэффициенты подгонки quintic не точно известны. Как ожидалось, результаты подгонки для poly3 разумны, потому что сгенерированные данные следуют за кубической кривой. 95% доверительных границ на подходящих коэффициентах указывают, что они приемлемо точны. Однако 95% доверительных границ для poly5 укажите, что подходящие коэффициенты не известны точно.
Статистические данные качества подгонки показывают в Таблице Подгонок. По умолчанию настроенный R-квадрат и статистика RMSE отображены в таблице. Статистические данные не показывают существенные различия между этими двумя уравнениями. Чтобы выбрать статистику, чтобы отобразиться или скрыться, щелкните правой кнопкой по заголовкам столбцов.
95%-е неодновременные границы предсказания для новых наблюдений показывают ниже. Чтобы отобразить границы предсказания в приложении Curve Fitting, выберите Tools> Prediction Bounds> 95%.
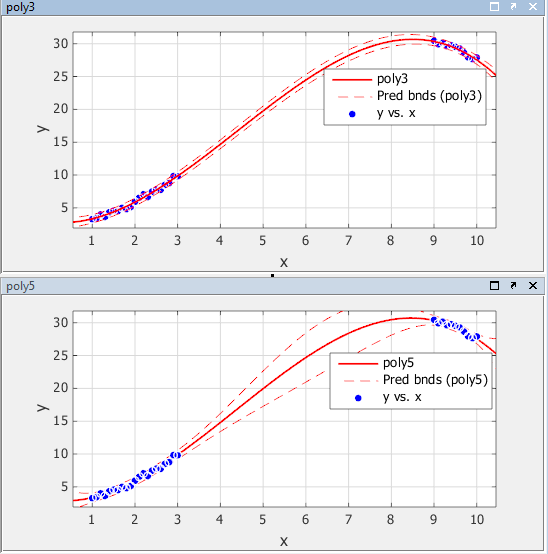
Предсказание ограничивает для poly3 укажите, что новые наблюдения могут быть предсказаны с маленькой неопределенностью в целой области значений данных. Дело обстоит не так для poly5. Это имеет более широкие границы предсказания в области, где никакие данные не существуют, по-видимому, потому что данные не содержат достаточно информации, чтобы оценить более высокие условия полинома степени точно. Другими словами, полином пятой степени сверхсоответствует данным.
95% предсказания ограничивают для подходящей функции с помощью poly5 показаны ниже. Как вы видите, неопределенность в предсказании, что функция является большой в центре данных. Поэтому вы пришли бы к заключению, что больше данных должно быть собрано, прежде чем можно будет сделать точные предсказания с помощью полинома пятой степени.
В заключение необходимо исследовать все доступные меры качества подгонки перед выбором подгонки, которая является лучшей в целях. Графическое исследование подгонки и остаточных значений должно всегда быть вашим начальным подходом. Однако некоторые подходящие характеристики показаны только через числовые результаты подгонки, статистику и границы предсказания.