Exponenta Banner

stcol

Рассеянный переводит матрицу словосочетания

Синтаксис

colmat = stcol(centers,x,type)
colmat = stcol(...,'tr')

Описание

colmat = stcol(centers,x,type) матрица чей (iJ) запись th

ψj(x(:,i)),    i=1:размер(x,2),j=1:n

с двумерными функциями ψj и номер n в зависимости от centers и вектор символов type, как детализировано в описании stmak.

centers и x должны быть матрицы с одинаковым числом строк.

Значение по умолчанию для type вектор символов 'tp', и для этого значения по умолчанию, n равняется size(centers,2), и функциями ψj дают

ψj(x)=ψ(x−centers(:,j)),   j=1:n

с ψ основная функция сплайна тонкой пластины

ψ(x)=|x|2log|x|2

и с |x | обозначение Евклидовой нормы векторного x.

Примечание

Смотрите stmak для описания других возможных значений для type.

Матричный colmat матрица коэффициентов в линейной системе

∑jajψj(x(:,i))=yi,   i=1:размер(x,2)

то, что коэффициенты, которым должен удовлетворить aj функционального f = Σjajψj, чтобы f интерполировал значение yi на сайте x(:,i), весь i.

colmat = stcol(...,'tr') возвращает транспонирование матрицы, возвращенной stcol(...).

Примеры

Пример 1. Следующее оценивает и строит функцию

f(x)=ψ(x−c1)+ψ(x−c2)+ψ(x−c3)−3.5ψ(x)

на регулярной mesh, с ψ вышеупомянутая основная функция тонкой пластины, и с c 1, c 2, c 3 три точки на модульном круге; см. рисунок ниже.

a = [0,2/3*pi,4/3*pi]; centers = [cos(a), 0; sin(a), 0];
[xx,yy] = ndgrid(linspace(-2,2,45)); 
xy = [xx(:) yy(:)].';
coefs = [1 1 1 -3.5];
zz = reshape( coefs*stcol(centers,xy,'tr') , size(xx));
surf(xx,yy,zz), view([240,15]), axis off

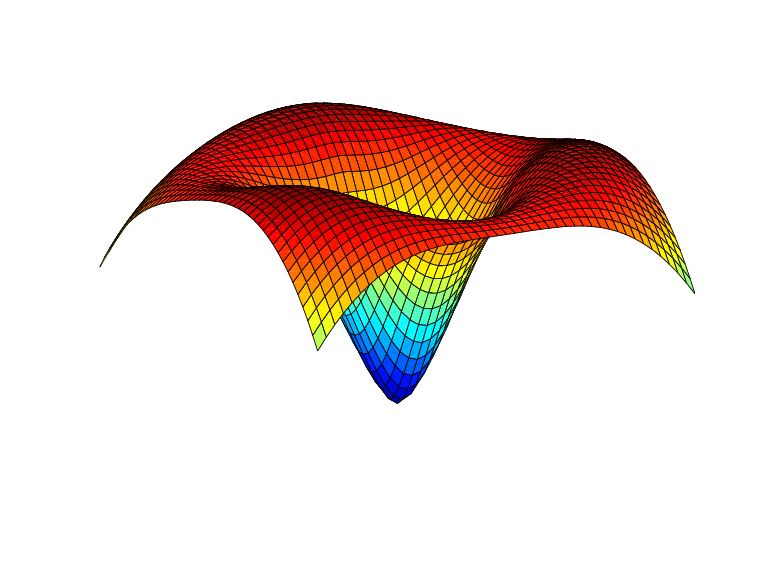
Пример 2. Следующее также оценивает, на той же mesh, и строит длину градиента функции в Примере 1.

zz = reshape( sqrt(...
        ([coefs,0]*stcol(centers,xy,'tp10','tr')).^2 + ...
        ([coefs,0]*stcol(centers,xy,'tr','tp01')).^2), 
size(xx));
figure, surf(xx,yy,zz), view([220,-15]), axis off

Смотрите также

|

Документация Curve Fitting Toolbox

Поддержка