Распределение Weibull широко используется в надежности и жизни (интенсивность отказов) анализ данных. Тулбокс предоставляет 2D параметру распределение Weibull
где a является масштабным коэффициентом, и b является параметром формы.
Обратите внимание на то, что существуют другие распределения Weibull, но необходимо создать пользовательское уравнение, чтобы использовать эти распределения:
Распределение Weibull с тремя параметрами с x, замененным x – c, где c является параметром положения
Адаптировано распределение Weibull с одним параметром, где параметр формы фиксируется и только масштабный коэффициент.
Curve Fitting Toolbox™ не строит распределения вероятности Weibull к выборке данных. Вместо этого это соответствует кривым к ответу и данным о предикторе, таким образом, что кривая имеет ту же форму как распределение Weibull.
Откройте приложение Curve Fitting путем ввода cftool. В качестве альтернативы нажмите Curve Fitting на вкладке Apps.
В приложении Curve Fitting выберите данные о кривой (X data и Y data, или только Y data против индекса).
Приложение Curve Fitting создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели от Polynomial к Weibull.
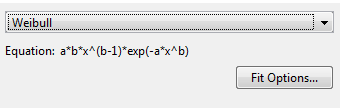
Нет никаких подходящих настроек, чтобы сконфигурировать.
(Необязательно) Нажмите Fit Options, чтобы задать содействующие начальные значения и ограничительные границы, или изменить настройки алгоритма.
Тулбокс вычисляет случайные стартовые точки для моделей Weibull, заданных на интервале [0,1]. Можно заменить стартовые точки и задать собственные значения в Подходящем Окне параметров.
Для получения дополнительной информации о настройках см. Опции Подгонки Определения и Оптимизированные Начальные точки.
Задайте тип модели weibull.
Например, чтобы загрузить некоторые данные в качестве примера, измеряющие концентрацию крови составного объекта против времени, и соответствовать и построить модель Weibull, задающую стартовую точку:
time = [ 0.1; 0.1; 0.3; 0.3; 1.3; 1.7; 2.1;...
2.6; 3.9; 3.9; ...
5.1; 5.6; 6.2; 6.4; 7.7; 8.1; 8.2;...
8.9; 9.0; 9.5; ...
9.6; 10.2; 10.3; 10.8; 11.2; 11.2; 11.2;...
11.7; 12.1; 12.3; ...
12.3; 13.1; 13.2; 13.4; 13.7; 14.0; 14.3;...
15.4; 16.1; 16.1; ...
16.4; 16.4; 16.7; 16.7; 17.5; 17.6; 18.1;...
18.5; 19.3; 19.7;];
conc = [0.01; 0.08; 0.13; 0.16; 0.55; 0.90; 1.11;...
1.62; 1.79; 1.59; ...
1.83; 1.68; 2.09; 2.17; 2.66; 2.08; 2.26;...
1.65; 1.70; 2.39; ...
2.08; 2.02; 1.65; 1.96; 1.91; 1.30; 1.62;...
1.57; 1.32; 1.56; ...
1.36; 1.05; 1.29; 1.32; 1.20; 1.10; 0.88;...
0.63; 0.69; 0.69; ...
0.49; 0.53; 0.42; 0.48; 0.41; 0.27; 0.36;...
0.33; 0.17; 0.20;];
f=fit(time, conc/25, 'Weibull', ...
'StartPoint', [0.01, 2] )
plot(f,time,conc/25, 'o');Если вы хотите изменить подходящие опции, такие как содействующие начальные значения, и ограничительные границы, подходящие для ваших данных, или изменить настройки алгоритма, видят таблицу дополнительных свойств с NonlinearLeastSquares на fitoptions страница с описанием.
Соответствующие значения стартовой точки и масштабирующийся conc/25 для 2D параметра модель Weibull были вычислены, подбирая 3 модели Weibull параметра с помощью этого пользовательского уравнения:
f=fit(time, conc, ' c*a*b*x^(b-1)*exp(-a*x^b)', 'StartPoint', [0.01, 2, 5] )
f =
General model:
f(x) = c*a*b*x^(b-1)*exp(-a*x^b)
Coefficients (with 95% confidence bounds):
a = 0.009854 (0.007465, 0.01224)
b = 2.003 (1.895, 2.11)
c = 25.65 (24.42, 26.89)
fit | fitoptions | fittype